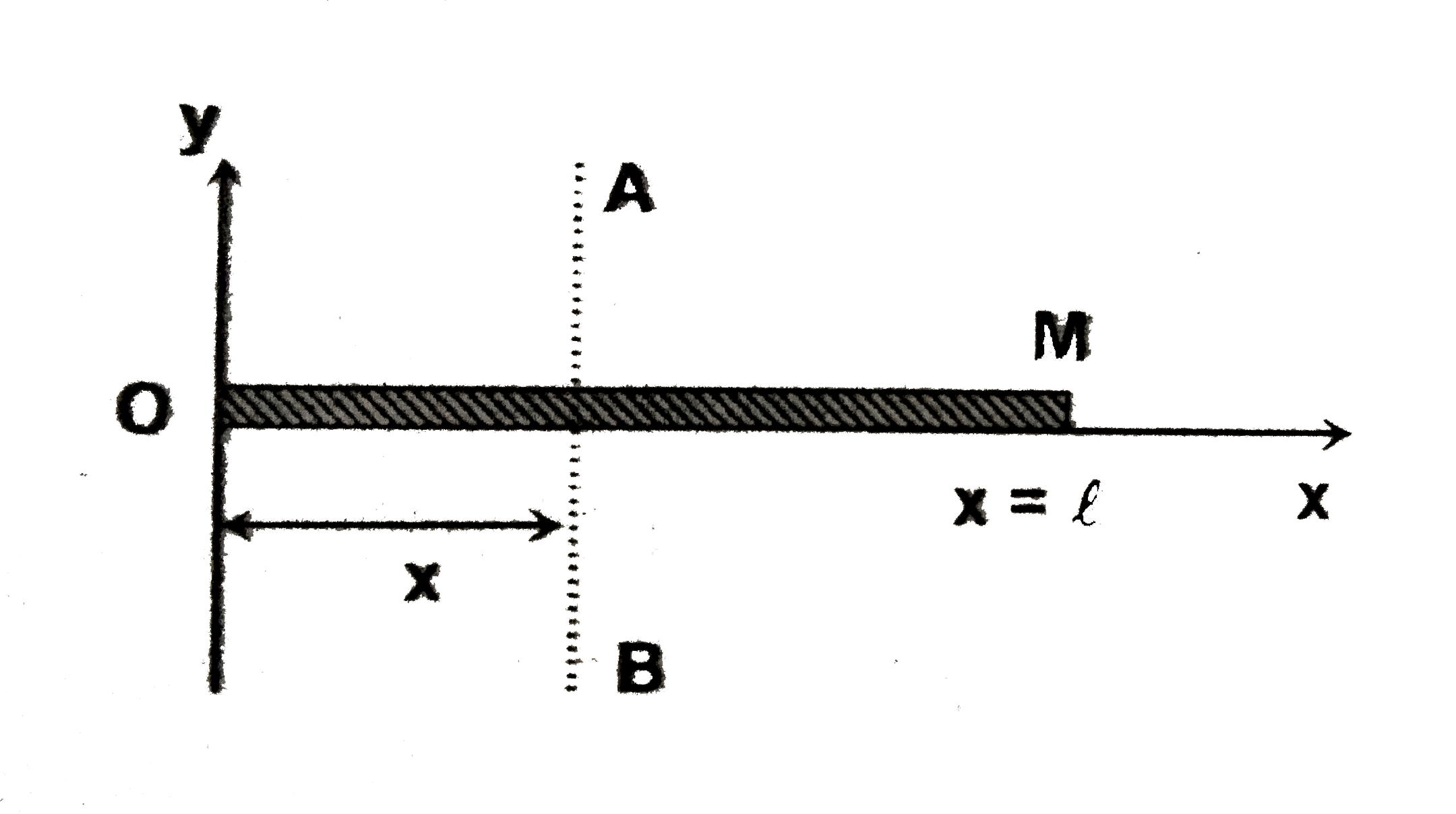
A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass densty that varies with the distance x from left end of the rod according to $λ = λ_{0} (\frac{x^{3}}{L^{3}})$
Where unit of $λ_{0}$ is kg/m. What is the value of x so that moment of inertia of rod about axis AB $(I_{A B})$ is minimum?

A

$\frac{7 l}{15}$

B

$\frac{2 l}{5}$

C

$\frac{8 l}{15}$

D

$\frac{4 l}{5}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

First method:
$I_{A B} = \int y^{2} d m = \frac{λ_{0}}{l^{3}} \int_{- x}^{l - x} {(y + x)}^{3} y^{2} d y$
$\int {(y + x)}^{3} y^{2} d y = y^{2} \frac{{(y + x)}^{4}}{4} - \frac{1}{2} y {(y + x)}^{4} d y$
$= \frac{y^{2} {(y + x)}^{2}}{4} - \frac{y}{10} {(y + x)}^{5} + \frac{1}{10} {(y + x)}^{5} d y$
$= \frac{y^{2} {(y + x)}^{2}}{4} - \frac{y {(x + y)}^{5}}{10} + \frac{{(y + x)}^{2}}{60}$
$\int_{- x_{0}}^{(l - x)} y^{2} {(y + x)}^{3} d x = \frac{{(L - x)}^{2} {(l)}^{4}}{4} - \frac{(l - x) l^{5}}{10} + \frac{l^{6}}{60}$
$I_{A B} = λ_{0} [\frac{{(l - x)}^{2}}{4} l - \frac{1}{10} (l - x) l^{2} + \frac{1}{60} l^{3}] = λ_{0} l [\frac{{(l - x)}^{2}}{4} l - \frac{1}{10} (l - x) + \frac{1}{60} l^{2}]$
$\frac{d l_{A B}}{d x} = 0 \Rightarrow - \frac{(l - x)}{2} + \frac{l}{10} = 0 \Rightarrow 5 l - 5 x = l \Rightarrow 5 x = 4 l \Rightarrow x = \frac{4 l}{5}$
Second method:
As we know that moment of inertial is minimum among all set of parallel axis, if axis is passing through centre of mass, so x must be distance of centre of mass.
$X_{C M} = \frac{1}{M} \int_{0}^{L} x d m$
$M = \int d m = \frac{λ_{0}}{l^{3}} l \int 0 x^{3} d x = \frac{λ_{0} l}{4}$ and $l \int 0 x d x = \frac{λ_{0}}{l^{3}} l \int 0 x^{4} d x = \frac{λ_{0} l^{2}}{5}$
Putting these values in equation (i) we have $x_{C M} = \frac{4 l}{5}$
Third method:
From given funtion it is clear that centre of mass of system must be at distance grater
that l/2. We have only two option $\frac{8 l}{15}$ and $\frac{4 l}{5}$ . For graph it is clear that maximum mass existence is nearer to other end, so it can't be $\frac{8 l}{15}$ , so right answer will be $\frac{4 l}{5}$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

A rod length $L$ and mass $M$ is placed along the $x$ -axis with one end at the origin, as shown in the figure above. The rod has linear mass density $λ = \frac{2 M}{L^{2}} x,$ where $x$ is the distance from the origin. Which of the following gives the $x$ -coordinate of the rod's center of mass?
A $\frac{2}{3} L$
B $\frac{1}{4} L$
C $\frac{1}{3} L$
D $\frac{1}{2} L$
A rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is
A ${0.16 kg - m}^{2}$
B ${0.12 kg - m}^{2}$
C ${0.32 kg - m}^{2}$
D ${0.08 kg - m}^{2}$
A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is $λ = λ_{0} x$ . The distance of centre of mass of rod from the origin is :
A $L / 2$
B $2 L / 3$
C $L / 4$
D $L / 5$

FIITJEE-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile