_E01_054_Q01.png)
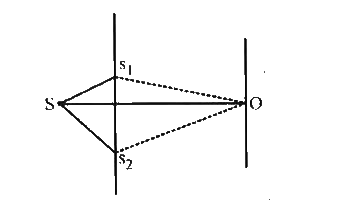
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-
3I
5I
8I
zero
The correct Answer is:A
_E01_054_S01.png)
d12=2πλ×λ6×2=2π3
d23=2πλ×λ2×2=2π
A'=
⎷(√32)2+(3A2)2=√3A
⇒I∝A2⇒A2R=3A2⇒IR=3I
Topper's Solved these Questions
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 3 (Miscellaneous type Questions)
27 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 4 A (Conceptual subjective Exercise)
9 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 1 (Check your Grasp)
75 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
In an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
View SolutionParallel monochromatic beam is falling normally on two slits S1 and S2 separated by d as shown in figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of S1S2 and S3S4. When z=Dλ2d, the intensity measured at P is I. and when z is equal to 4Dλd, Intensity is xl. Find x.
View Solution
Knowledge Check
In the figure shown S1O−S2O=S3O−S2O=λ4, Intensity at O due to any one of the slits is I0. What is the intensity due to all the three coherent sources S1,S2andS3 ?
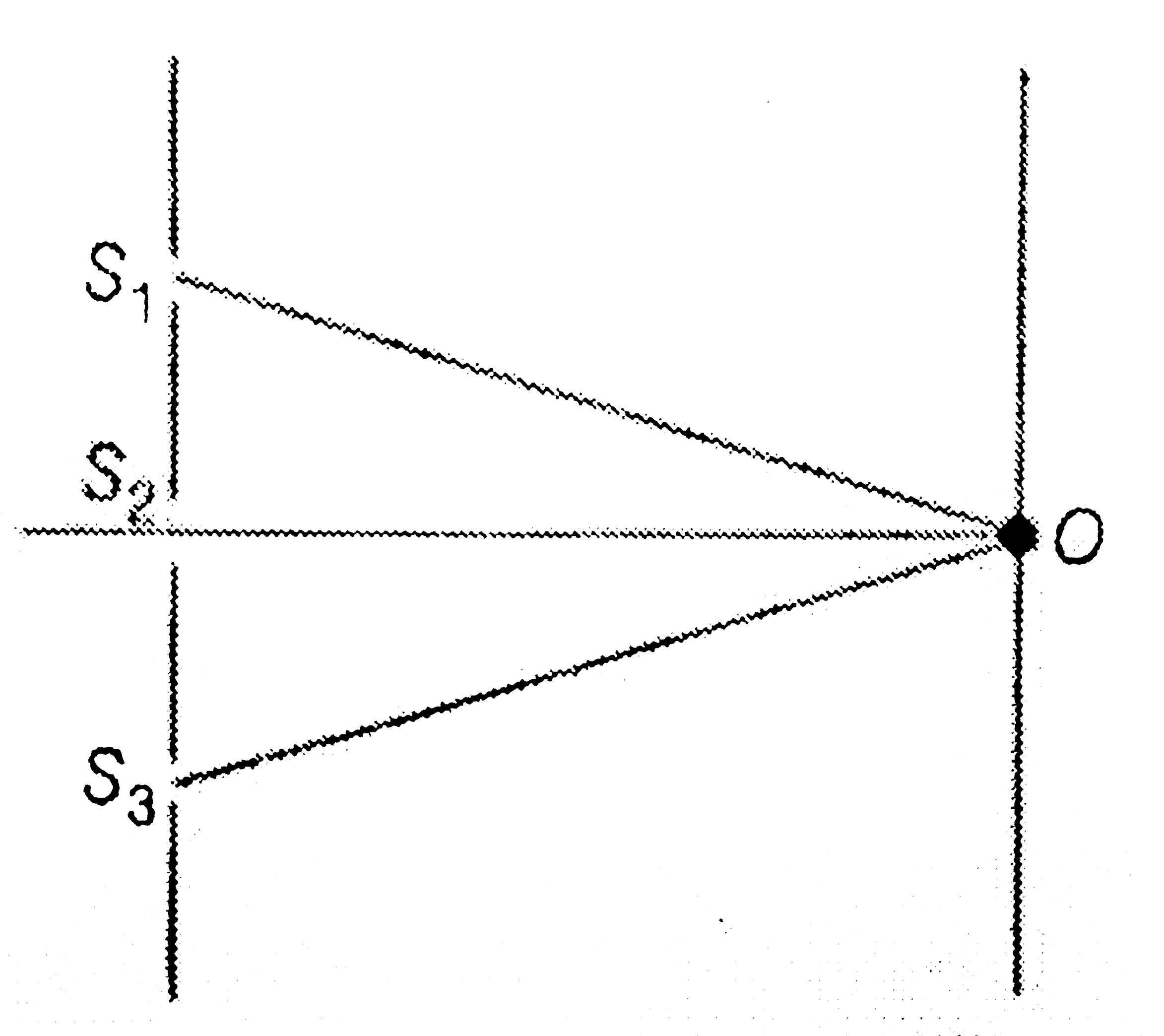A3I0BI0C5I0D9I0Two sound waves each of wavelength λ and having the same amplitude A form two sources S1andS2 interfere at a point P. If the path difference S2P−S1P=λ3, then the amplitude of the resultant were at P will be
AAB2ACA/2D3A/2In arrangement shown in figure, plane wavefront of monochromatic light of wavelength λ is incident on identical slits S1 and S2. There is another pair of indentical slits S3 and S4 which are having separation Z=λD2d Point O is on the screen at the common perpendicular bisector of S1S2 and S3S4.I1 is the intensity at point O Now the board having slits S3S4 is moved upward parallel to itself and perpendicular to line AO till slit S4 is on line AO and it is observed that now intensity at point O is I2 then I2I1 is :
A12B2C1D0
Consider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d
View SolutionMonochromatic light of wavelength λ passes through a very narrow slit S and then strikes a screen placed at a distance D = 1m in which there are two parallel slits S1 and S2 as shown. Slit S1 is directly in line with S while S2 is displaced a distance d to one side. The light is detected at point P on a second screen, equidistant from S1 and S2 When either slit S1 or S2 is open equal light intensities I are measured at point P. When both slits are open, the intensity is three times as large i.e. 3I. If the minimum possible wavelength is Nd2, then find the value of N(d<<D)
View SolutionIn the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
View SolutionColumn I shows four situations of standard Young’s double slit arrangement with the screen placed far away from the slits S1 and S2 . In each of these cases S1P0=S2P0,S1P1−S2P1=λ/4 and S1P2−S2P2=λ/3, where λ is the wavelength of the light used. In the cases B,C and D, a transparent sheet of refractive index μ and thickness t is pasted on slit S1 . The thicknesses of the sheets are different in different cases. The phase difference between the light waves reaching a point P on the screen from the two slits is denoted by δ(P) and the intensity by I(P). Match each situation given in Column I with the statement(s) in Column II valid for that situation.
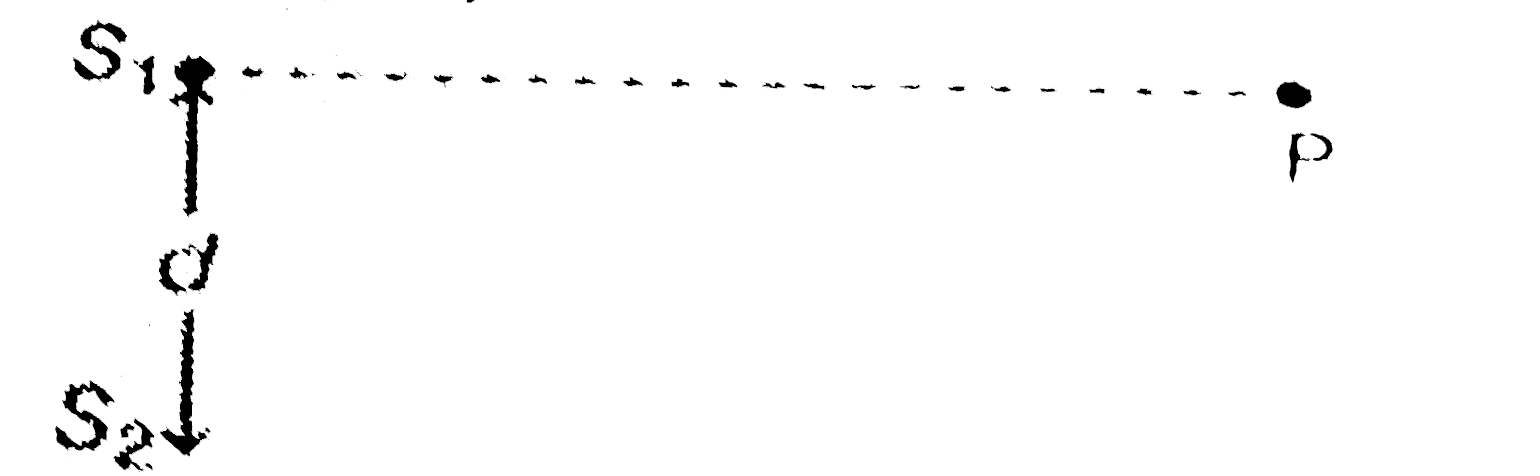
View SolutionConsider two coherent monochromatic (wavelength λ) sources S1andS2 separated by a distance d. The ratio of intensity of S1 and that of S2 at point P is 4. The distance of P from S1 if the resultant intensity at point P is equal to 94, times the intensity due to S1 is : (n is a positive integer )
View Solution