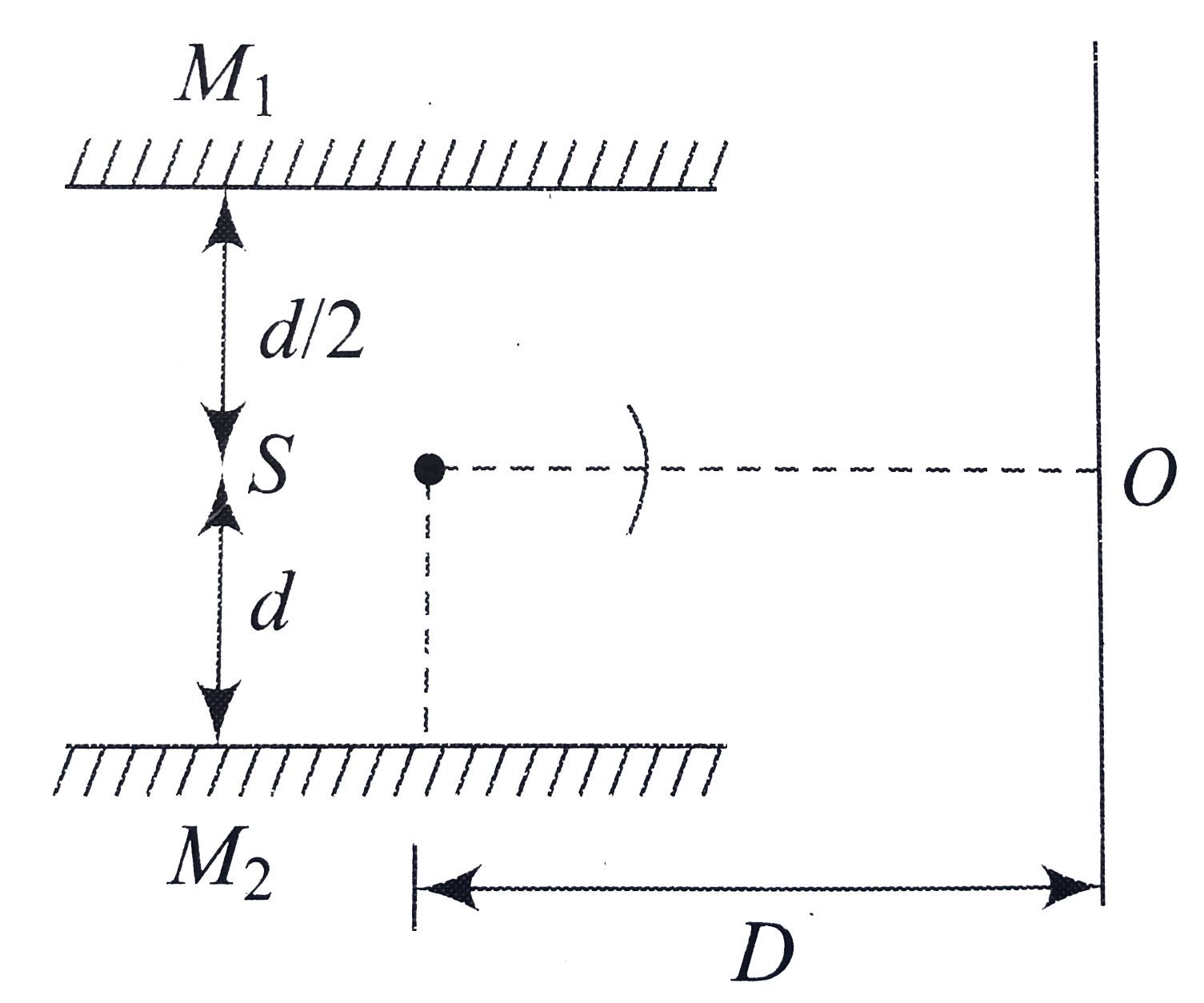
M1 and M2 are plane mirrors and kept parallel to each other. At point O, there will be a maxima for wavelength λ. Light from a monochromatic sources S of wavelength λ is not reaching directly on the screen. Then, λ is
3d2D
3d22D
d2D
2d2D
The correct Answer is:B
_E01_047_S01.png)
For reflected light waves the two virtual source (images of source in mirror) at a distance 3d
path difference at O=S2O−S1O
√D2+(2d)2−√D2+d2=λ
⇒D2+4d2=D2+d2+λ2+2√D2+d2λ
⇒3d2=2Dλ⇒λ=3d22D
Topper's Solved these Questions
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 3 (Miscellaneous type Questions)
Explore 27 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 4 A (Conceptual subjective Exercise)
Explore 9 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 1 (Check your Grasp)
Explore 75 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
Similar Questions
When a metal is illuminated by light of wavelength λ , the stopping potential is V∘ and for wavelength 2λ, it is 3V∘.Then the threshold wavelength is ?
View SolutionTwo particles move at right angle to each other.Their de Broglie wavelengths are lambda_(1) and lambda_(2) respectively.The particles suffer perfectly inelastic collision.The de Broglie wavelength lambda of the final particle is given by :
View Solution
Knowledge Check
M1 and M2 are two plane mirrors which are kept parallel to each other as shown. There is a point 'O' on perpendicular screen just infront of 'S'. What should be the wavelength of light coming from monchromatic source 'S'. So that a maxima is formed at 'O' due to interference of reflected light from both the mirrors. [Consider only 1st reflection]. [D>>d,d>>λ]
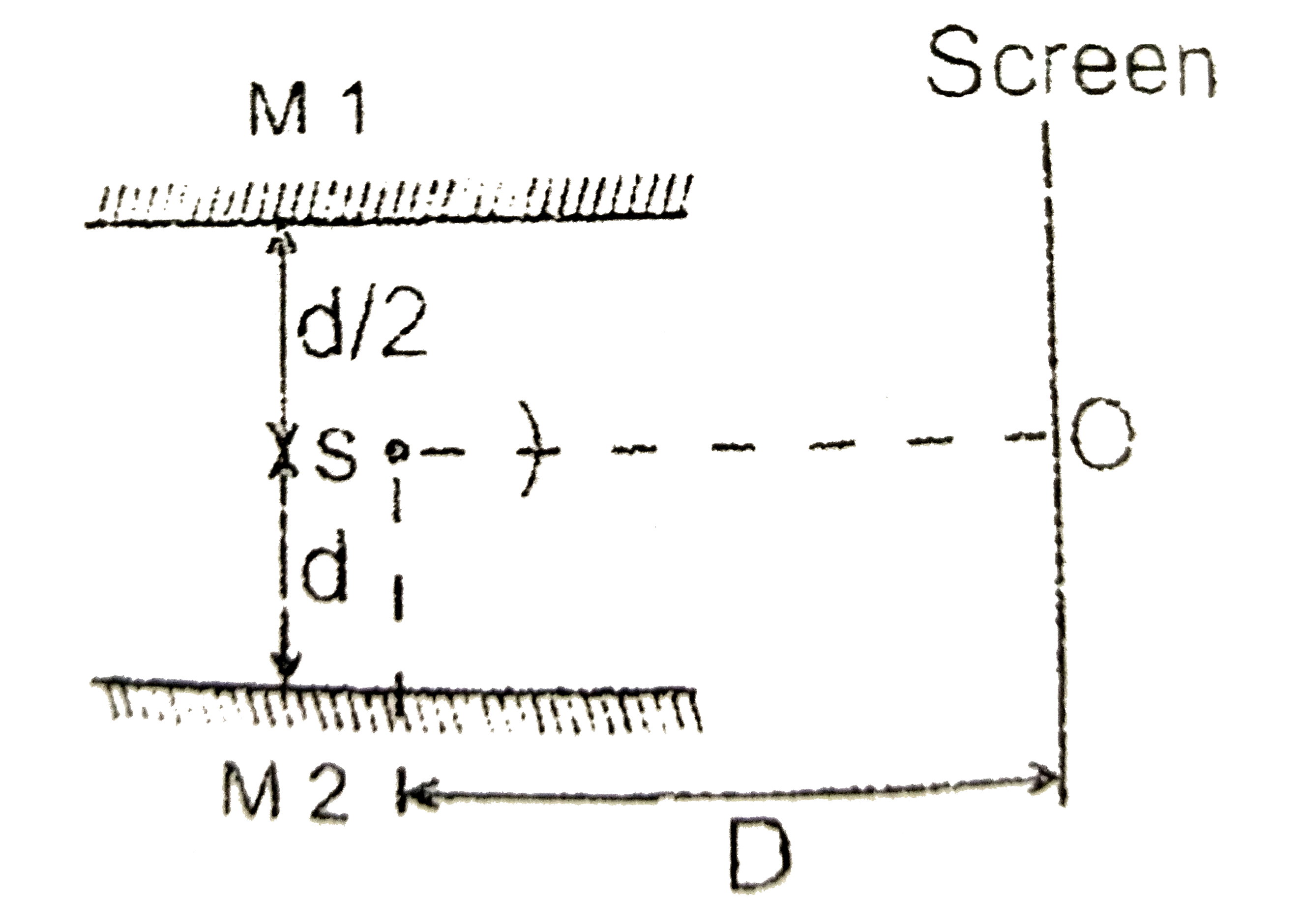 A3d2DB3d22DCd2DD2d2D
A3d2DB3d22DCd2DD2d2DTwo mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.
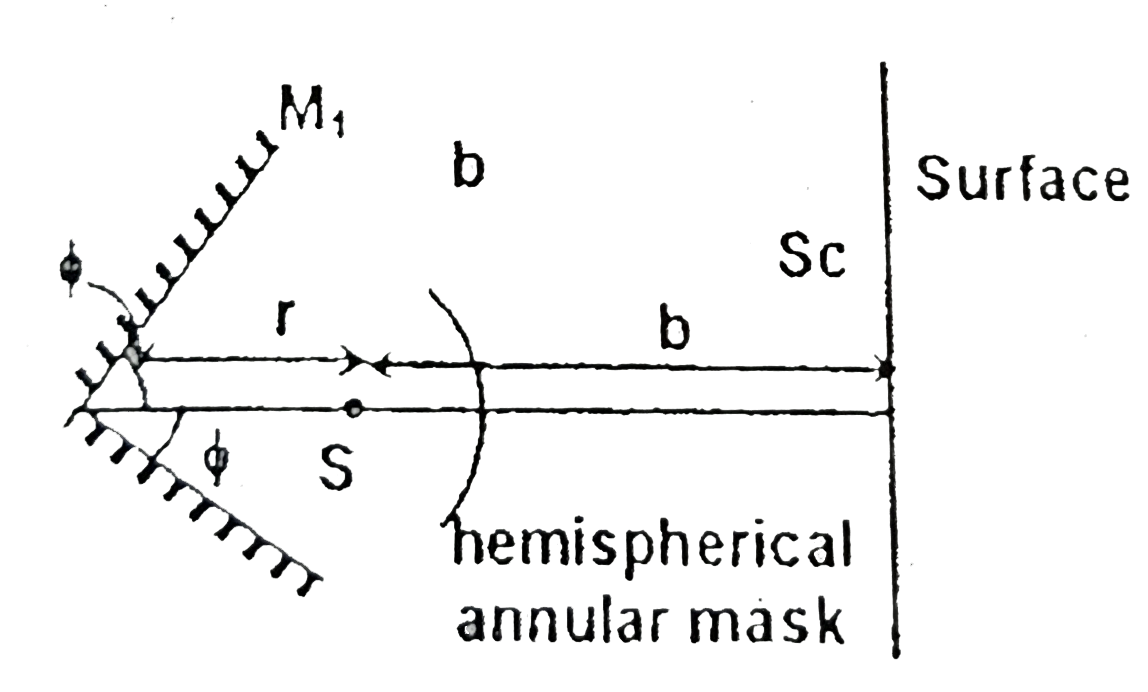 Aλ(b+2rsin2ϕ)2rsin2ϕBλ(b+2rcos2ϕ)2rsin2ϕCλ(b+rcos2ϕ)2rsin2ϕDλ(b+2rcos2ϕ)rsin2ϕ
Aλ(b+2rsin2ϕ)2rsin2ϕBλ(b+2rcos2ϕ)2rsin2ϕCλ(b+rcos2ϕ)2rsin2ϕDλ(b+2rcos2ϕ)rsin2ϕA beam o monochromatic light of wavelength λ is reflected from air into water to refractive index 4/3. The wavelength of light beam inside water will be
A916×λB3λ/4Cλ×43Dλ
Light beams of wavelengths λandλ' are illuminated on a single slit of aperture a. If the value of λ is 5×10−7m, the first maxima formed coincides with the first minima formed light of wavelength λ'. Calculate the value of λ'.
View SolutionTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
View SolutionThree coherent point sources S1,S2andS3 are placed on a line perpendicular to the screen as shown in the figure. The wavelength of the light emitted by the sources is lambda. The distance between adjacent sources is d=3λ The distance of S2 from the screen is D(>>λ). Find the minimum (non zero) distance x of a point P on the screen at which complete darkness is obtained.

View SolutionA ray of light of wavelength λ is incident on mirror at an angle of incidence 60∘. The wavelength of light after reflection will be
View SolutionWhen a point light source, of power W, emiting monochromatic light of wavelength λ is kept at a distance a from a small photosensitive surface of work function ϕ and area S. Then
View Solution
