A rectangular, a square , a circular and an elliptical loop, all in the (x−y) plane, are moving out of a uniform magnetic field with a contant velocity →v=vˆi . The magnetic field is directed along the negative z-axis direction. The induced emf, during the passege of these loops , out of the field region, will not remain constant for
the rectangular, circular and elliptical loops
the circular and the elliptical loops
only the elliptical loop
any of the four loops
The correct Answer is:B
To solve the problem, we need to analyze the induced electromotive force (emf) in each of the given loops (rectangular, square, circular, and elliptical) as they move out of a uniform magnetic field. The magnetic field is directed along the negative z-axis, and the loops are moving with a constant velocity in the x-direction.
1. Understanding the Setup:
- We have four types of loops: rectangular, square, circular, and elliptical.
- All loops are in the x-y plane and are moving out of a uniform magnetic field directed along the negative z-axis.
2. Induced EMF Formula:
- The induced emf (E) in a loop can be calculated using Faraday's law of electromagnetic induction, which states:
E=−dΦBdt
- Here, ΦB is the magnetic flux through the loop, given by:
ΦB=B⋅A
- Where B is the magnetic field strength and A is the area of the loop within the magnetic field.
3. Analyzing Each Loop:
- Rectangular Loop:
- As the rectangular loop moves out of the magnetic field, a constant width (breadth) of the loop is exiting the field at a constant velocity. The area exiting per unit time remains constant.
- Thus, the induced emf will remain constant.
- Square Loop:
- Similar to the rectangular loop, the square loop has a constant width and length. As it exits the magnetic field, the area change per unit time is constant.
- Therefore, the induced emf will also remain constant.
- Circular Loop:
- For the circular loop, as it exits the magnetic field, the area that exits is not uniform. The edge of the circle that is exiting changes as the loop moves, leading to a varying area exiting the field.
- Hence, the induced emf will not remain constant.
- Elliptical Loop:
- The elliptical loop behaves similarly to the circular loop. As it moves out of the magnetic field, the area that exits changes non-uniformly due to the shape of the ellipse.
- Thus, the induced emf will also not remain constant.
4. Conclusion:
- The induced emf will remain constant for the rectangular and square loops but will not remain constant for the circular and elliptical loops.
- Therefore, the answer to the question is that the induced emf will not remain constant for the circular and elliptical loops.
Final Answer:
The induced emf will not remain constant for the circular and elliptical loops.
- We have four types of loops: rectangular, square, circular, and elliptical.
- All loops are in the x-y plane and are moving out of a uniform magnetic field directed along the negative z-axis.
- The induced emf (E) in a loop can be calculated using Faraday's law of electromagnetic induction, which states:
E=−dΦBdt
- Here, ΦB is the magnetic flux through the loop, given by:
ΦB=B⋅A
- Where B is the magnetic field strength and A is the area of the loop within the magnetic field.
- Rectangular Loop:
- As the rectangular loop moves out of the magnetic field, a constant width (breadth) of the loop is exiting the field at a constant velocity. The area exiting per unit time remains constant.
- Thus, the induced emf will remain constant.
- Similar to the rectangular loop, the square loop has a constant width and length. As it exits the magnetic field, the area change per unit time is constant.
- Therefore, the induced emf will also remain constant.
- For the circular loop, as it exits the magnetic field, the area that exits is not uniform. The edge of the circle that is exiting changes as the loop moves, leading to a varying area exiting the field.
- Hence, the induced emf will not remain constant.
- The elliptical loop behaves similarly to the circular loop. As it moves out of the magnetic field, the area that exits changes non-uniformly due to the shape of the ellipse.
- Thus, the induced emf will also not remain constant.
- The induced emf will remain constant for the rectangular and square loops but will not remain constant for the circular and elliptical loops.
- Therefore, the answer to the question is that the induced emf will not remain constant for the circular and elliptical loops.
The induced emf will not remain constant for the circular and elliptical loops.
Topper's Solved these Questions
Similar Questions
As shown in Fig. 6.26, a rectangular loop and a circular loop are moving out of a uniform magnetic field region to a field free region with a constant velocity v. In which loop do you expect the induced emf to be constant during the passage out of the field region ? The field is normal to the loops.
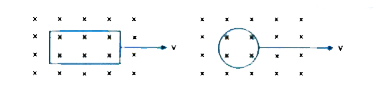
View SolutionA closed loop with the geometry shown in Fig. 3.9 is placed in a uniform magnetic field direction into the plane of the paper. If the magnetic field decreases with time, determine the direction of the induced emf in this loop.

View Solution
Knowledge Check
A rectangular, a square, a circular and an elliptical loop, all in the x-y plane, are moving out of a uniform magnetic field with a constant velocity vcev=v0ˆi. The magnetic field is directed along the negative z-axis direction. The induced emf, during the passage of these loops, out of the field region, will not remain constant for
Athe rectangular, circular and elliptical loops.Bthe circular and the elliptical loops.Conly the elliptical loop.Dany of the four loops.
Emf induced in the left arm of the loop, if it is moved out of the magnetic field in 1s with constant speedA0.1VB2VC1VD0.2VAn electron moving with a uniform velocity along the positive x-direction enters a magnetic field directed along the positive y-direction. The force on the electron is directed along
APositive y− directionBNegative y-directionCPositive z- directionDNegative z-direction
(a) A closed loop is held stationary in the magnetic field between the north and south poles of two permanent magnets held fixed. Can we hope to generate current in the loop by using very strong magnets?
(b) A closed loop moves normal to the constant electric field between the plates of a large capacitor. Is a current induced in the loop (i) when it is wholly inside the region between the capacitor plates (ii) when it is partially outside the plates of the capacitor? The electric field is normal to the plane of the loop.
(c) A rectangular loop and a circular loop are moving out of a uniform magnetic field region (Fig. 6.8) to a field-free region with a constant velocity v. In which loop do you expect the induced emf to be constant during the passage out of the field region? The field is normal to the loops.

(d) Predict the polarity of the capacitor in the situation described by Fig. 6.9.

View SolutionAnswer the following quesitons : (a) A closed conducting loop moves normal to the electric fieldd between the plates of a large capacitor. Is a current induced in the loop when it is (i) wholly inside the capacitor (ii) partially outside the plates of capacitor. Electric field is normal to the plane of the loop.
(b) A rectangular loop and a circular loop are moving out of a uniform magnetic field region to a field free region with a constant velocity, Fig. In which loop do you expact the induced e.m.f. to be constant during the passage out of the field region, the field is normal to the loops ?
(c ) Predict the polarity of the capacitor in the situation described by Fig.
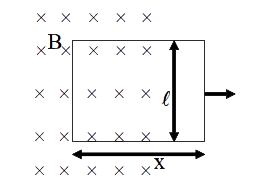
View SolutionA rectangular loop of resistance R, and sides l and X, is pulled out of a uniform magnetic field B with a for maintaining uniform velocity of withdrawal is __
View SolutionA proton is moving along the negative direction of X-axis in a magnetic field directed along the positive direction of Y-axis. The proton will be deflected along the negative direction of
View SolutionA neutral metal bare moves at a constant velocity v to the right through a region of uniform magnetic field directed out the page, as shown. Therefore,

View Solution

