A neutral metal bare moves at a constant velocity v to the right through a region of uniform magnetic field directed out the page, as shown. Therefore,

positive charges accumulate to the left side and negative charges to the right side of the rod
negative charges accumulate to the left side and positive charges to the right side of the rod
positive charges accumulate to the top end and negative charges to the bottom end of the rod
negative charges accumulate to the top end and positive charges to the bottom end of the rod
The correct Answer is:D
Step by step video, text & image solution for A neutral metal bare moves at a constant velocity v to the right through a region of uniform magnetic field directed out the page, as shown. Therefore, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
An electron does not suffer any deflection while passing through a region of uniform magnetic field. What is the direction of the magnetic field?
View SolutionAn electron does not suffer any deflection while passing through a region of uniform magnetic field. What is the direction of the magnetic field ?
View Solution
Knowledge Check
The counductor AD moves to the right in a uniform magnetic field directed into the plane of the paper.
 A(a) The free electron in AD will move toward AB(b) D will acquire a positive potential with respect to AC(c ) A current will flow from A→D in AD in closed loopD(d) The current in AD flows from lower to higher potential
A(a) The free electron in AD will move toward AB(b) D will acquire a positive potential with respect to AC(c ) A current will flow from A→D in AD in closed loopD(d) The current in AD flows from lower to higher potentialA particle of mass m and charge q moves with a constant velocity v along the positive x direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x=a to x=b. The minimum value of v required so that the particle can just enter the region x>b is
AqbBmBq(b−a)BmCqaBmDq(b+a)B2mA particle of the mass m and cgharge q moves with a constant velocity v along the positive x−direction.Itentersaregionconta∈∈gauniformmag≠ticfieldBdirectedalongtheminiμmvalueofvrequiredsotˆthepartic≤canjustentertheregion xgtb is
AqbBmBq(b−A)BmCqaBmDq(b+a)B2m
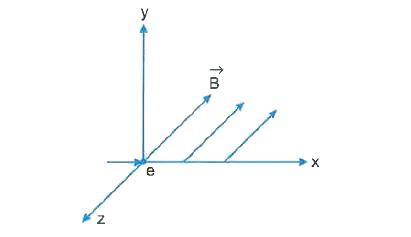
An electron moves along +x direction. It enters into a region of uniform magnetic field B directed along - z direction as shown in figure. Draw the shape of trajectory followed by the electron after entering the field.
View SolutionTwo straight conducting rails form a right angle where their ends are joined. A conducting bar in contact with the rails starts at the vertex at time t = 0 and moves with constant velocity v along them as shown in Fig. A magnetic field →B is directed into the page. the induced emf in the circuit at any time t is proportional to

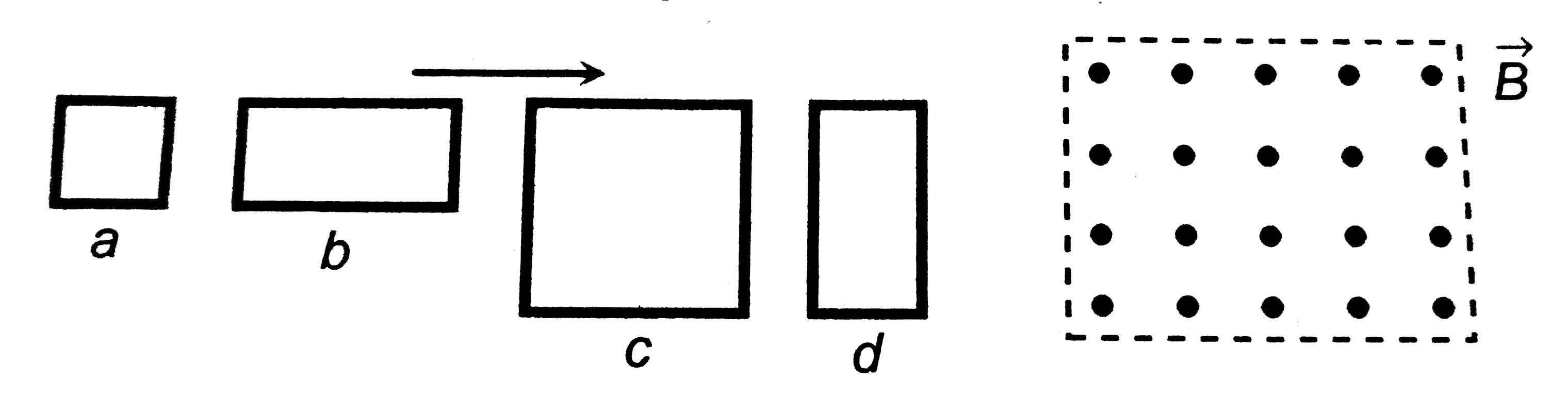
View SolutionThe figure shows four wire loops, with edge length of either L or 2L. All four loops will move through a region of uniform magnetic field →B (directed out of the page) at the same constant velocity . Rank the four loops according to the maximum magnitude of the e.m.f. induced as they move through the field, greatest first
View SolutionA metal rod moves at a constant velocity in a direction perpendicular to its length. A constant, uniform magnetic field exists in space in a direction perpendicular to the rod as well as its velocity. Select the correct statements(s) from the following
View SolutionA conducting loop is pulled with a constant velocity towards a region of uniform magnetic field as shown in the figure then the current involved in the loop is (d>r) -

View Solution

