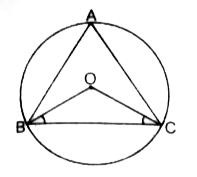
BC is a chord with centre O. A is a point on an arc BC . Prove that: ∠BAC+∠OBC=90 , if A is the point on the major arc.
Video Solution
Text Solution
The arc BC for the ∠BOC=z on the center of circle and ∠BAC=x and z=2x
Now apply the property of angle sum property of triangle
In △BOC
∠OBC+∠OCB+∠BOC=180⋅
y+y+z=180⋅
2y+2x=180⋅
x+y=90⋅
Hence, ∠BAC+∠OBC=90⋅
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
P and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
A80∘B200∘C160∘D100∘ABC is an equilateral triangle inscribed in a circle. D is any point on the arc BC. What is ∠ADB equal to?
A90∘B60∘C45∘DNone of theseC is a point on the minor arc AB a circle with centre O. If ∠AOB=100∘, what is ∠ACB ?
A80∘B90∘C100∘D130∘
The circumcentre of the ΔABC is O. Prove that ∠OBC+∠BAC=90∘.
View SolutionBC is a chord to a circle with centre O. A is a point on major are BC as shown in the below figure. What is the value of ∠BAC+∠OBC ?
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn the figure, BC is a chord of the circle with centre o and A is a point on the minor are BC. Then ∠ABC−∠OBCis equal to
View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc
View Solution

