Show that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.

Video Solution

Text Solution

Verified by Experts

Solution
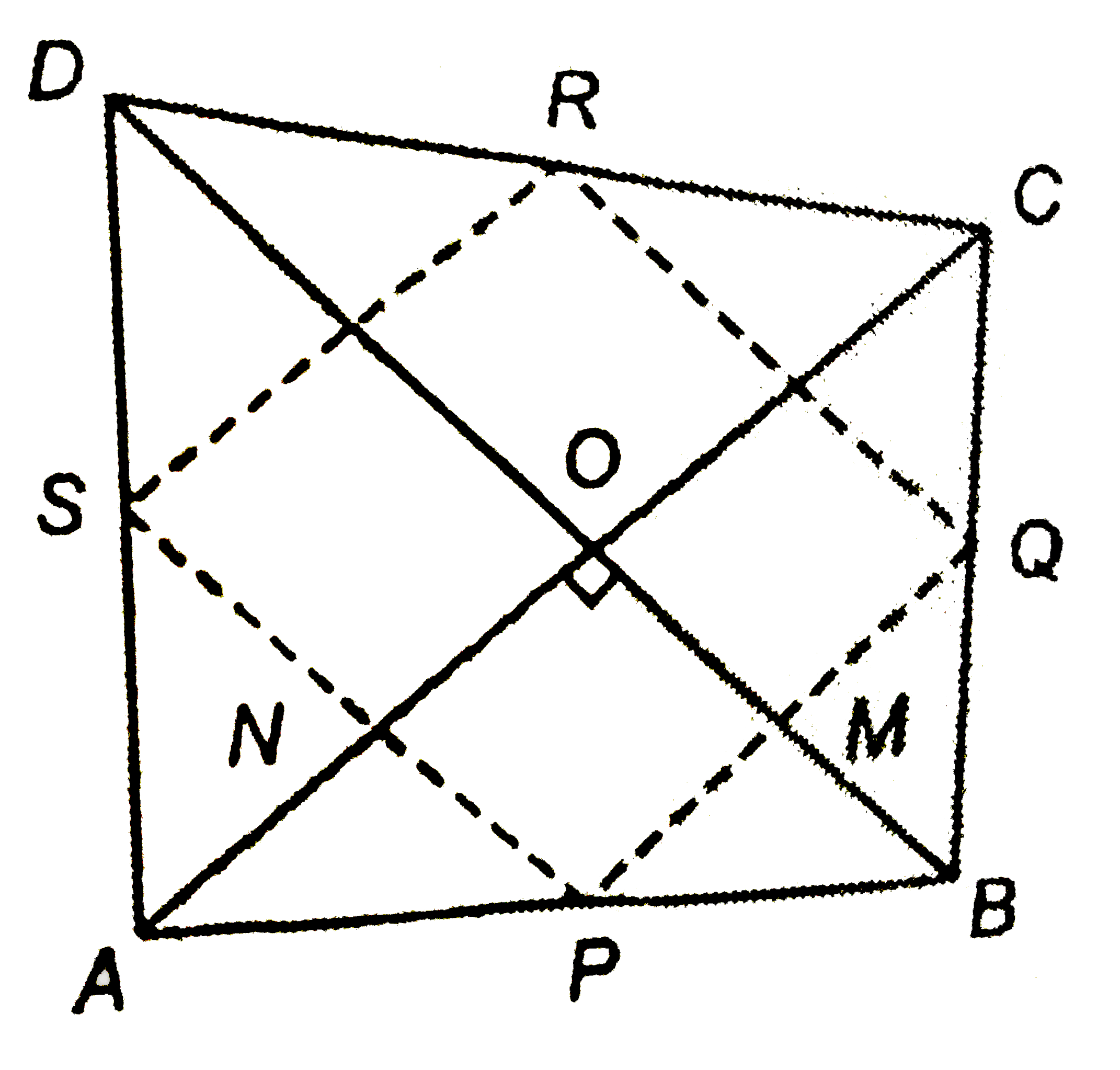
In a square $A B C D, P, Q, R$ and $S$ are the mid-points of $A B, B C, C D$ and $D A$ respectively.
⇒ $A B = B C = C D = A D$ [ Sides of square are equal ]
In $△ A D C$ ,
$S R ∥ A C and S R = \frac{1}{2} A C$ [ By mid-point theorem ] ---- ( 1 )
In $△ A B C$ ,
$P Q ∥ A C$ and $P Q = \frac{1}{2} A C$ [ By mid-point theorem ] ---- ( 2 )
From equation ( 1 ) and ( 2 ),
$S R ∥ P Q$ and $S R = P Q = \frac{1}{2} A C$ ---- ( 3 )
Similarly, $S P ∥ B D$ and $B D ∥ R Q$
∴ $S P ∥ R Q$ and $S P = \frac{1}{2} B D$
and $R Q = \frac{1}{2} B D$
∴ $S P = R Q = \frac{1}{2} B D$
Since, diagonals of a square bisect each other at right angle.
∴ $A C = B D$
⇒ $S P = R Q = \frac{1}{2} A C$ ----- ( 4 )
From ( 3 ) and ( 4 )
$S R = P Q = S P = R Q$
We know that the diagonals of a square bisect each other at right angles.
$∠ E O F = 90 \circ$
Now, $R Q ∥ D B$
$R E ∥ F O$
Also, $S R ∥ A C$
⇒ $F R ∥ O E$
∴ $O E R F$ is a parallelogram.
So, $∠ F R E = ∠ E O F = 90 \circ$ (Opposite angles are equal)
Thus, $P Q R S$ is a parallelogram with $∠ R = 90 \circ$ and $S R = P Q = S P = R Q$
∴ $P Q R S$ is a square.

Updated on:21/07/2023

The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if
APQRS is a rectangle
BPQRS is parallelogram
Cdiagonals of PQRS are perpendicular
Ddiagonals of PQRS are equal
The quadrilateral formed by joining the midpoints of the sides of a quadrilateral ABCD, taken in order, is a rectangle, if
AABCD is a parallelogram
BABCD is a rectangle
Cdiagonals of ABCD are equal
Ddiagonals of ABCD are perpendicular to each other
The quadrilateral formed by joining the midpoints of the sides of a quadrilateral ABCD, taken in order, is a rhombus, if
AABCD is a parallelogram
BABCD is a rectangle
Cdiagonals of ABCD are equal
Ddiagonals of ABCD are perpendicular to each other