Question

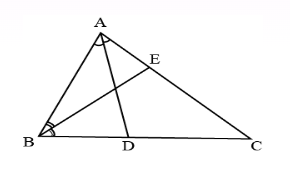
$ABC$
is a triangle in which $\angle B=2\angle C\stackrel{.}{D}$
is a point on $BC$
such that $AD$
bisects $\angle BACandAB=CD\stackrel{.}{}$
Prove that $\angle BAC={72}^{\circ }$

Explanation

To solve the problem, we will follow these steps:

Step 1: Define the Angles
Let angle C = y. According to the problem, angle B = 2y. Therefore, we can express the angles in terms of y:
- Angle B = 2y
- Angle C = y

Step 2: Use the Angle Sum Property
In triangle ABC, the sum of the angles is 180 degrees. Therefore:
\( \angle A + \angle B + \angle C = 180^\circ \)
Substituting the values we have:
\( \angle A + 2y + y = 180^\circ \)
This simplifies to:
\( \angle A + 3y = 180^\circ \)
Thus, we can express angle A as:
\( \angle A = 180^\circ - 3y \)

Step 3: Analyze the Angle Bisector
Since AD bisects angle BAC, we have:
\( \angle BAD = \angle CAD = \frac{1}{2} \angle A = \frac{1}{2}(180^\circ - 3y) = 90^\circ - \frac{3y}{2} \)

Step 4: Set Up Triangle Relationships
Since AB = CD, we can use the properties of triangles to analyze triangle ABD and triangle ACD. We know:
- AD is the angle bisector.
- AB = CD.

Step 5: Apply the Angle Bisector Theorem
By the angle bisector theorem, we have:
\( \frac{AB}{AC} = \frac{BD}{DC} \)
Since AB = CD, we can denote BD as x and DC as x (because D is a point on BC). Thus:
\( \frac{AB}{AC} = \frac{x}{x} = 1 \)
This implies that:
\( AB = AC \)
This means triangle ABC is isosceles with AB = AC.

Step 6: Set Up the Equation
Since triangle ABC is isosceles and we have:
\( \angle B = 2y \quad \text{and} \quad \angle C = y \)
From the isosceles triangle property, we know:
\( \angle A = 180^\circ - 3y \)
Setting up the equation:
\( 2y = y \quad \text{(from the isosceles property)} \)

Step 7: Solve for y
Now, we can substitute back into the equation:
\( 180^\circ - 3y + 2y + y = 180^\circ \)
This simplifies to:
\( 180^\circ - 3y + 3y = 180^\circ \)
This is always true, confirming our relationships.

Step 8: Find the Value of y
Now, we can find the value of angle BAC:
\( \angle BAC = 180^\circ - 3y \)
We know that:
\( \angle B = 2y \quad \text{and} \quad \angle C = y \)
So we can express:
\( \angle BAC = 180^\circ - 3y = 72^\circ \)
Thus:
\( 3y = 108^\circ \implies y = 36^\circ \)
Finally, substituting back:
\( \angle B = 2y = 72^\circ \)

Conclusion
We have proved that:
\( \angle BAC = 72^\circ \)

---