If ABC
is an isosceles triangle such that AB=AC
and AD
is an altitude from A
on BC
. Prove that
(i) ∠B=∠C
(ii) AD
bisects BC
(iii) AD
bisects ∠A
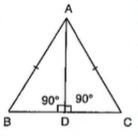
"Given: ABC is an isosceles triangle in which AB=AC.
To Prove: (i) ∠B=∠C
(ii) AD bisects BC
(iii) AD bisects ∠A
Proof : In △ABDandACD
AB=AC (Given)
AD=AD (Common)
△ADB=△ADC (each 90⋅)
△ADB≅△ACD (by RHS)
(i) ∠B=∠C (By CPCT)
(ii) DB=DC
AD bisects BC
(iii) ∠BAD=∠CAD
AD bisects ∠A
Topper's Solved these Questions
Similar Questions
Knowledge Check
In an isosceles triangle ΔABC,AB=AC and ∠A=80∘. The bisector of ∠Band∠C meet at D. The ∠BDC is equal to the
A90∘B100∘C130∘D80∘
In Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.

View SolutionABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD∣∣AB. Show that(i) ∠DAC=∠BCA and (ii) ABCD is a parallelogram.
View SolutionIn an isosceles triangle ABC , if AB=AC=25cm and BC=14cm , then the measure of altitude from A on BC is (a) 20cm (b) 22cm (c) 18cm (d) 24cm
View SolutionIn ABC,∠A=900andAD is an altitude. Complete the relation BDDA=AB() .
View SolutionIn ΔABC prove that (i)a=bcosC+ccosB (ii)b=ccosA+acosC (iii) c=acosB+bcosA
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View SolutionLet ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE
View Solution