In quadrilateral ACBD, AC=AD and AB bisects ∠A . Show that ABC ≅ABD. What can you say about BC and BD?
To solve the problem, we need to show that triangles ABC and ABD are congruent, and then determine the relationship between BC and BD.
1. Identify the Given Information:
- In quadrilateral ACBD:
- AC=AD (given)
- AB bisects ∠A (which means ∠CAB=∠DAB)
2. Label the Angles:
- Let ∠CAB=∠DAB=x (since AB bisects ∠A)
3. Write Down the Known Sides and Angles:
- We have:
- AC=AD (given)
- AB=AB (common side)
- ∠CAB=∠DAB (since AB bisects ∠A)
4. Apply the SAS Congruence Criterion:
- We can now apply the Side-Angle-Side (SAS) criterion for triangle congruence:
- Side 1: AC=AD
- Angle: ∠CAB=∠DAB
- Side 2: AB=AB (common side)
- Therefore, by the SAS criterion, we conclude that:
△ABC≅△ABD
5. Conclude About the Corresponding Sides:
- By the property of congruent triangles (CPCTC - Corresponding Parts of Congruent Triangles are Congruent), we can state that:
BC=BD
Final Conclusion:
- We have shown that △ABC≅△ABD using the SAS criterion, and thus BC is equal to BD.
- In quadrilateral ACBD:
- AC=AD (given)
- AB bisects ∠A (which means ∠CAB=∠DAB)
- Let ∠CAB=∠DAB=x (since AB bisects ∠A)
- We have:
- AC=AD (given)
- AB=AB (common side)
- ∠CAB=∠DAB (since AB bisects ∠A)
- We can now apply the Side-Angle-Side (SAS) criterion for triangle congruence:
- Side 1: AC=AD
- Angle: ∠CAB=∠DAB
- Side 2: AB=AB (common side)
- Therefore, by the SAS criterion, we conclude that:
△ABC≅△ABD
- By the property of congruent triangles (CPCTC - Corresponding Parts of Congruent Triangles are Congruent), we can state that:
BC=BD
- We have shown that △ABC≅△ABD using the SAS criterion, and thus BC is equal to BD.
Topper's Solved these Questions
Similar Questions
In quadrilateral ACBD, AC = ADand AB bisects ∠A(see Fig. 7.16). Show that ΔABC≅ΔABD

View SolutionThe diagonals of quadrilateral ABCD,ACandBD intersect in O. Prove that if BO=OD, the triangles ABCandADC are equal in area.
View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
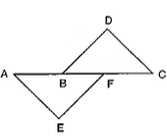
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
View SolutionIn ABC, ∠B=600,∠C=400, AL⊥BC and AD bisects ∠A such that L and D lie on side BC. Find ∠LAD.
View SolutionBD is one of the diagonals of a quadrilateral ABCD. AM and CN are the perpendiculars from A and C , respectively, on BD. Show That ar (qua..ABCD)=12BD.AM+CN
View SolutionIn a cyclic quadrilateral ABCD, if AB ∣∣ CD and ∠B=70∘, find the remaining angles.
View SolutionABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at P. If AB=DC, prove that:
(i)PAB ≅PDC
(ii)PA=PD and PC=PB (iii) AD∣∣BC
View Solution