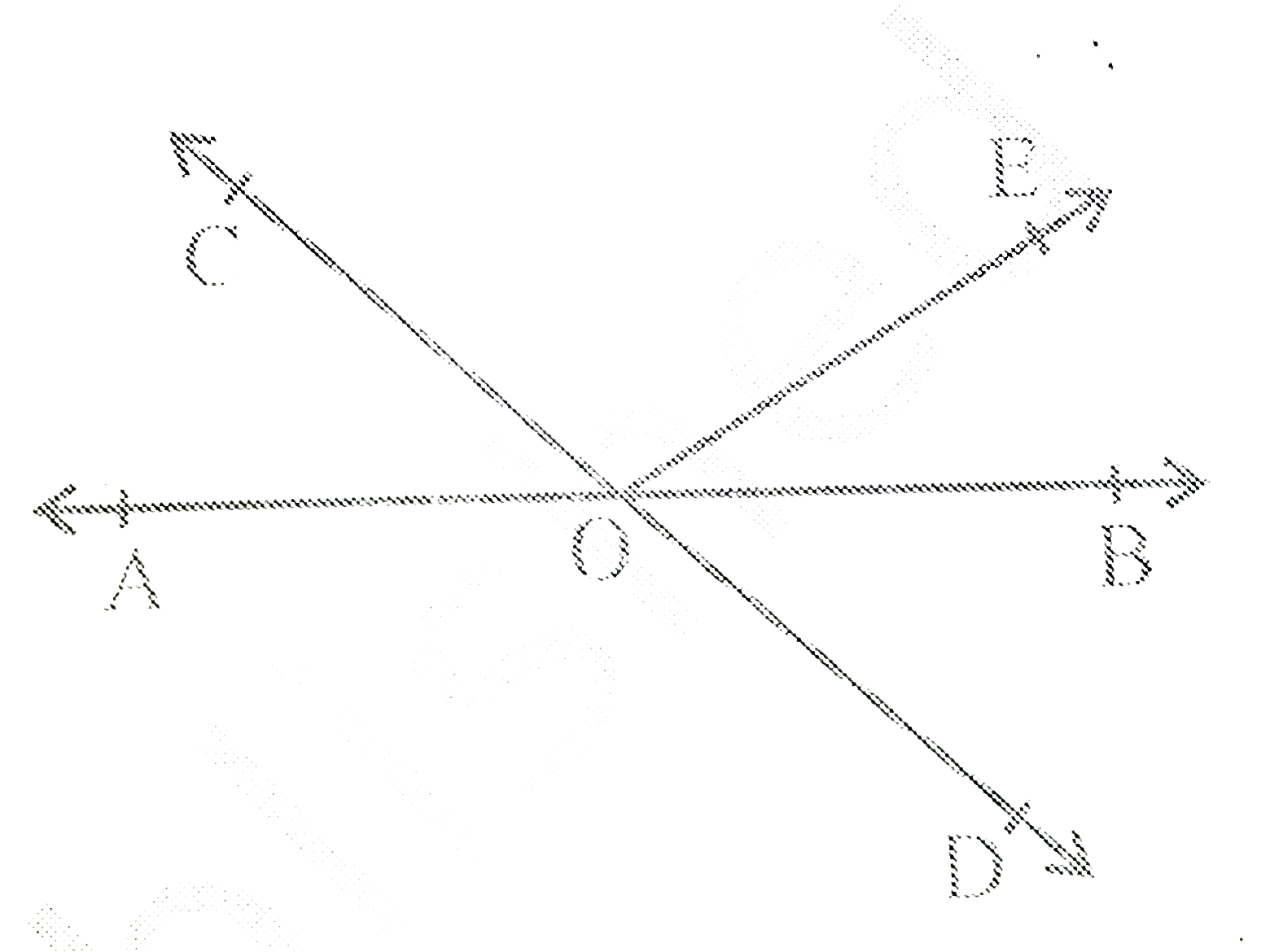Two lines AB and CD intersect at O. If ∠AOC+∠COB+∠BOD=270∘ , find the measures of ∠AOC, ∠COB, ∠BOD and ∠DOA.
To solve the problem, we need to find the measures of angles ∠AOC, ∠COB, ∠BOD, and ∠DOA given that:
∠AOC+∠COB+∠BOD=270∘
1. Understanding the Angles:
When two lines intersect, they form four angles around the point of intersection. The total measure of these angles is 360∘.
∠AOC+∠COB+∠BOD+∠DOA=360∘
2. Using the Given Information:
We know from the problem statement that:
∠AOC+∠COB+∠BOD=270∘
3. Finding ∠DOA:
We can substitute the sum of the angles we know into the total angle equation:
270∘+∠DOA=360∘
To find ∠DOA, we rearrange the equation:
∠DOA=360∘−270∘=90∘
4. Identifying Vertically Opposite Angles:
Since AB and CD intersect at point O, the angles opposite each other are equal. Therefore:
∠AOC=∠BOD(vertically opposite angles)
∠COB=∠DOA(vertically opposite angles)
5. Using the Linear Pair Property:
Since CD is a straight line, the angles ∠COB and ∠BOD are supplementary:
∠COB+∠BOD=180∘
6. Substituting Known Values:
We already found ∠DOA=90∘, which means:
∠COB=90∘
7. Finding ∠BOD:
Using the linear pair property:
∠COB+∠BOD=180∘⟹90∘+∠BOD=180∘
Thus,
∠BOD=180∘−90∘=90∘
8. Finding ∠AOC:
Since ∠AOC=∠BOD:
∠AOC=90∘
Summary of Angles:
- ∠AOC=90∘
- ∠COB=90∘
- ∠BOD=90∘
- ∠DOA=90∘
When two lines intersect, they form four angles around the point of intersection. The total measure of these angles is 360∘.
We know from the problem statement that:
We can substitute the sum of the angles we know into the total angle equation:
Since AB and CD intersect at point O, the angles opposite each other are equal. Therefore:
∠COB=∠DOA(vertically opposite angles)
Since CD is a straight line, the angles ∠COB and ∠BOD are supplementary:
We already found ∠DOA=90∘, which means:
Using the linear pair property:
Since ∠AOC=∠BOD:
- ∠AOC=90∘
- ∠COB=90∘
- ∠BOD=90∘
- ∠DOA=90∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a quadrilateral ABCD, the bisectors of ∠A and ∠B meet at O. If ∠C=70∘and∠D=130∘, then measure of ∠AOBis
A40∘B60∘C80∘D100∘
If Figure, ∠AOF and ∠FOG form a linear pair. ∠EOB= ∠FOC=9000and ∠DOC= ∠FOG= ∠AOB=300 Find the measure of ∠FOE, ∠COB and ∠DOE. Name all the right angles. Name three pairs of adjacent complementary angles. Name three pairs of adjacent supplementary angles. Name three pairs of adjacent angles.
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800
View SolutionLine segments AB and CD intersect at O such that AC∣∣DB . If ∠CAB=350 and ∠CDB=550 find the ∠BOD.
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8 cm and BD=5.6cm . Find the measures of OC and OD
View SolutionIn figure, ΔODCΔOBA,∠BOC=125oand ∠CDO=70o. Find∠DOC,∠DCOand∠OAB.
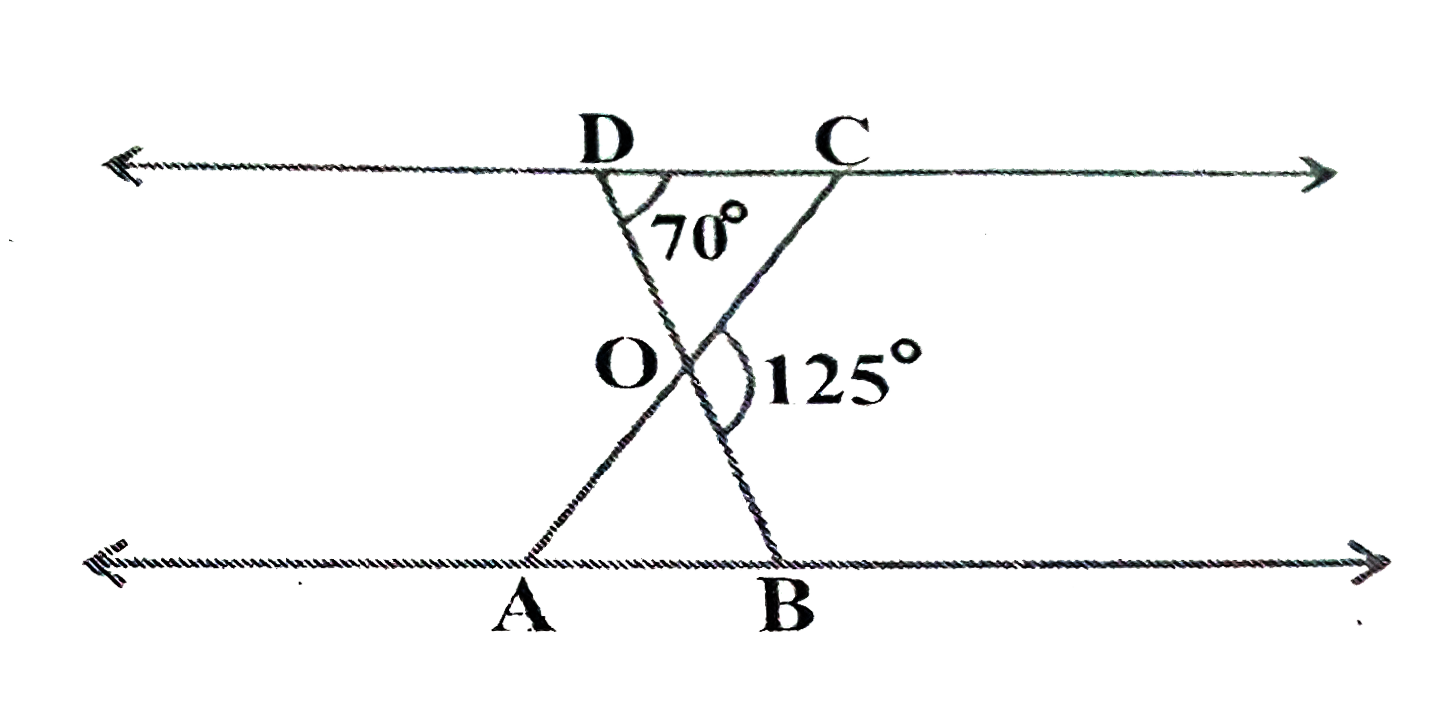
View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View Solution