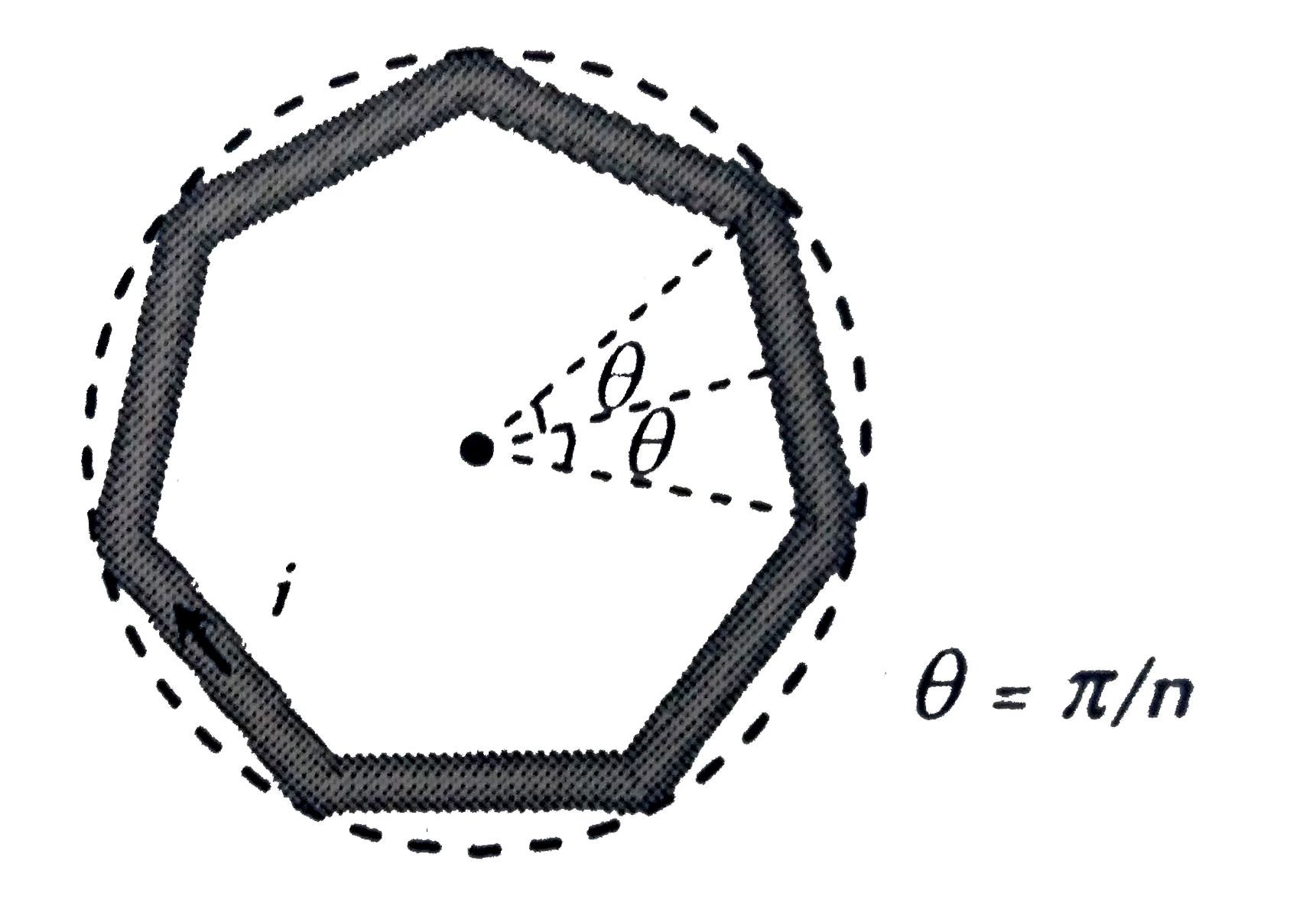
In the following figure a wire bent in the form of a regular polygon o

A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fidl induction at the center of polygon due to one side of the polygon is
A $\frac{μ_{0} I}{π R} (\frac{tan π}{n})$
B $\frac{μ_{0} I}{4 π R} \frac{tan π}{n}$
C $\frac{μ_{0} I}{2 π R} (\frac{tan π}{n})$
D $\frac{μ_{0} I}{2 π R} (\frac{cos π}{n})$
If a thin wire of length L is given the shape of a regular polygon of n sides and current I flows through it, what will be the net magnetic field at the centre of the polygon if n is infinity?
A $\frac{μ_{0} n i}{2 L}$
B $\frac{μ_{0} n i}{2 π L}$
C $\frac{μ_{0} π i}{L}$
D $\frac{μ_{0} n π i}{L}$
A wire of length l, carrying current i, is bent in circle of radius r, then magnetic momennt at centre of loop is
A $\frac{l^{2} i}{2 π}$
B $\frac{l^{2} i}{4 π}$
C $\frac{l i^{2}}{2 π}$
D $\frac{l i}{4 π}$

In the following figure a wire bent in the form of a regular polygon of $n$ sides is inscribed in a circle of radius $a$ . Net magnetic field at centre will be