A non-conducting rod having circular cross section of radius R is suspended from a rigid support as shown in fig. A light and small coil of 300turns is wrapped tightly at the left end where uniform magnetic filed B exists in vertically downward direction. Air of density ρ hits the half of the right part of the rod with velocity V as shown in the fig. What should be current in clockwise direction (as seen from O) in the coil so that rod remains horizontal? Give answer in mA. Given 2Lv√πRBρ=1√5A−1/2.
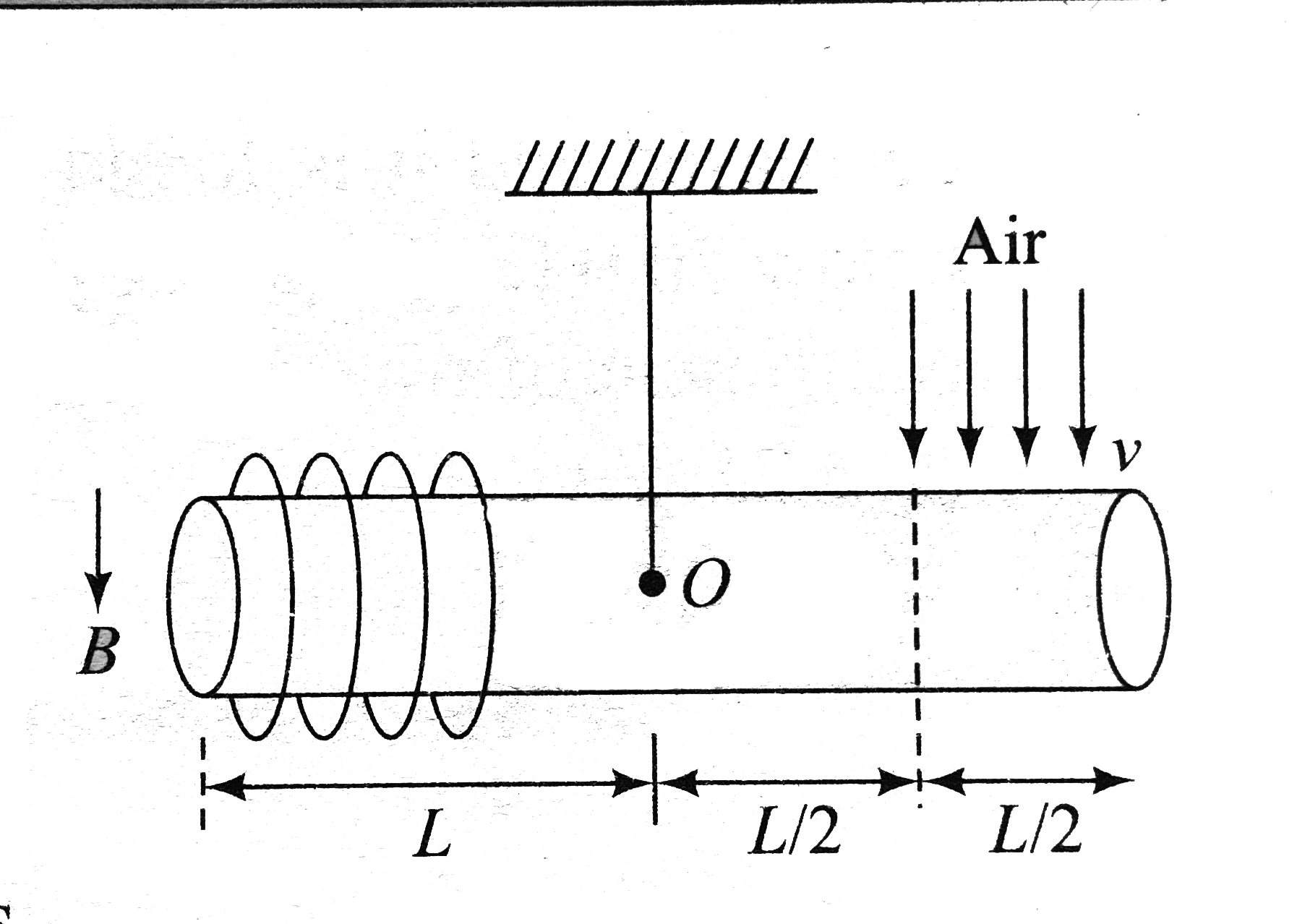
0.01A
0.1A
0.02A
0.2A
The correct Answer is:A
Force exerted by air on the rod
=ρ(L/3×2R)υ2=ρLRυ2
Balancing torque about O,
NI(πR2)=(ρLRυ2)×3L4
⇒300πBR=3ρυ2L24
⇒1=1400×ρL2υ2πBR=0.01A.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-VI (SINGLE ANSWER QUESTION)
81 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level =I (H.W)
42 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT Based Questions
20 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
Uniform magnetic field B, exists in the vertical downward direction. A rod whose length is kept horizontal and is moved with velocity v perpendicular to its length. Motional emf developed across the length of the rod is
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View Solution
Knowledge Check
A small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __
 AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heating
AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heatingA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 A(a) zero, when θ is zeroB(b) πa2Bω2R, when θ is zeroC( c) zero, when θ=π/2D(d) πa2Bω2R, when θ=π/2
A(a) zero, when θ is zeroB(b) πa2Bω2R, when θ is zeroC( c) zero, when θ=π/2D(d) πa2Bω2R, when θ=π/2Three light rods from a right angled triangle. The tension in the rod PR, if a force of 300N is applied vertically downward at R is.
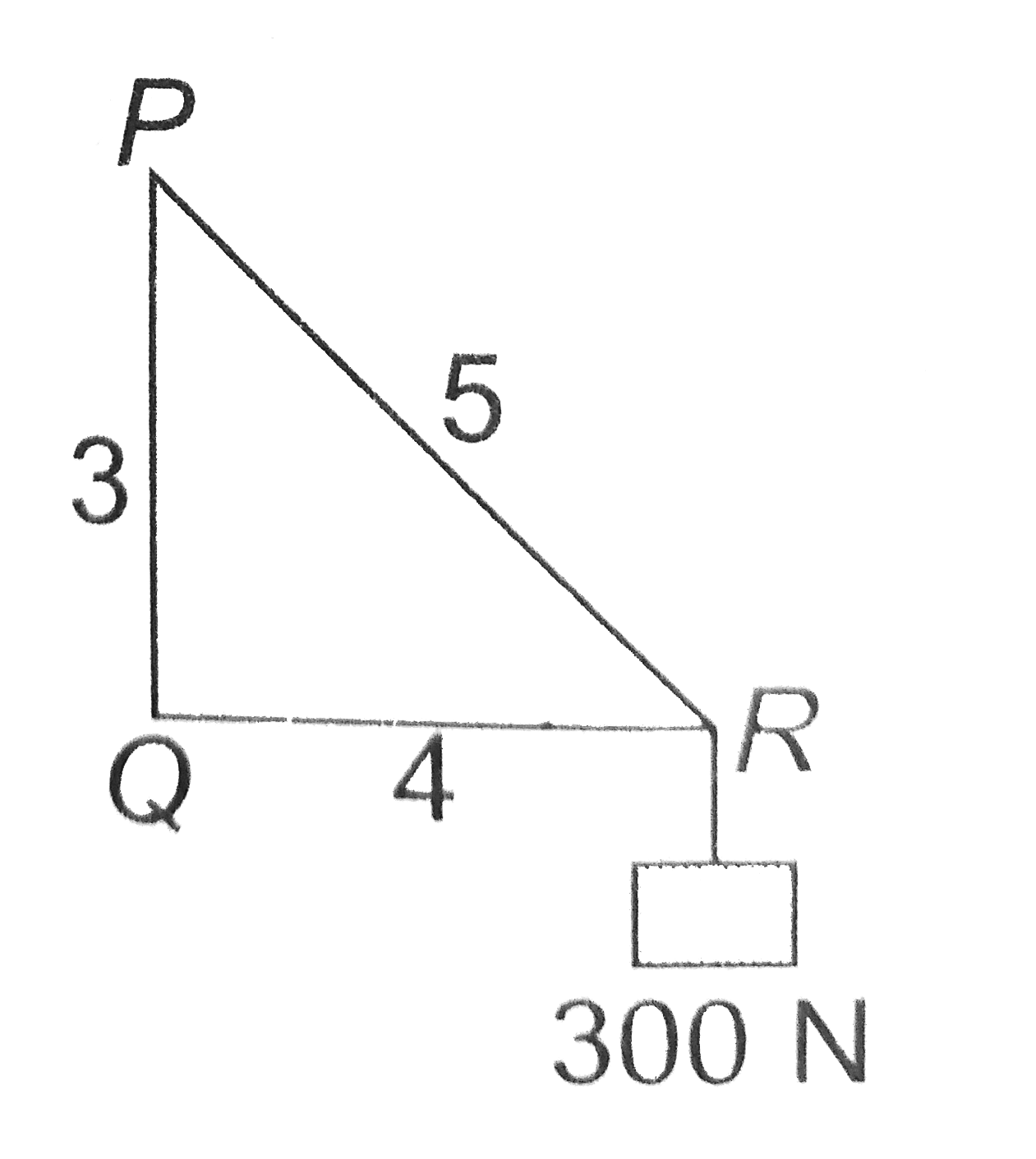 A400NB200NC300ND500N
A400NB200NC300ND500N
One end of a uniform rod of mass M and cross-sectional area A is suspended from a rigid support and an equal mass M is suspended from the other end, what is the stress at the mid point of the rod.
View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View SolutionA circular loop of radius a having n turns is kept in a horizontal plane. A uniform magnetic field B exists in a vertical direction as shown in Fig.313. Find the emf induced in the loop if the loop is roated with a uniform angualr velocity ω about
(a) an axis passing through the center and perendicular to the plane of the loop.
(b) the diameter.

View SolutionA circular coil of radius R is moving in a magnetic filed B with a velocity v as shown in the figure.

Find the emf across the diametrically opposite points A and B.
View SolutionA rod PQ is connected to the capacitor plates. The rod is placed in a magnetic field (B) directed downwards perpendicular to the plane of the paper. If the rod is pulled out of magnetic field with velocity →v as shown in Figure.
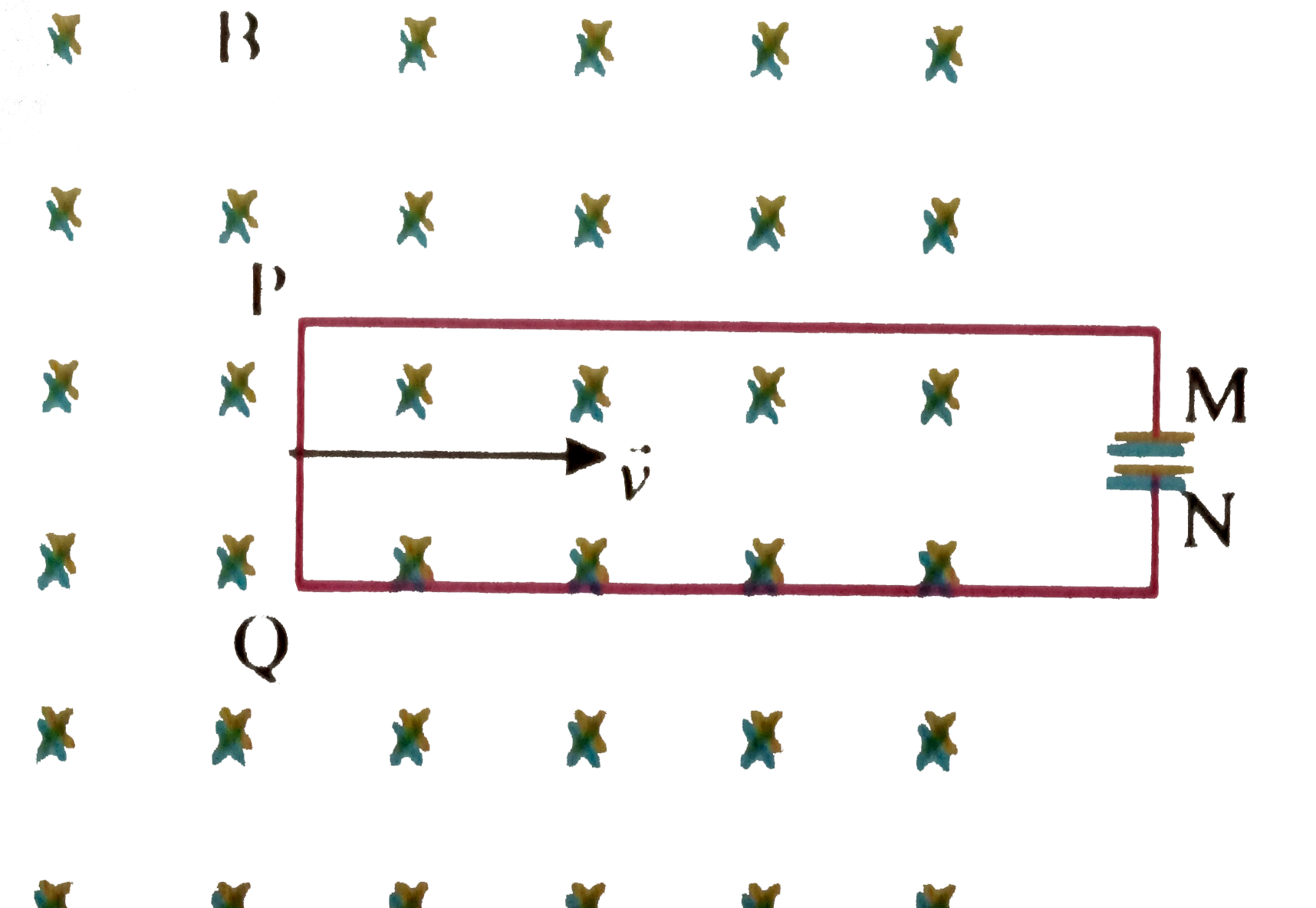
View Solution
