A current carrying wire frame is in the shape of digit eight (8). It is carrying current i0. If the radius of each loop is R0, then the net magnetic dipole moment of the figure is :

(i0πR20)√2
zero
i0×2πR20
i0×(4πR0)
The correct Answer is:B
Area vector both the loops are in opposite direction.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-VI (SINGLE ANSWER QUESTION)
Explore 81 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level =I (H.W)
Explore 42 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:NCERT Based Questions
Explore 20 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
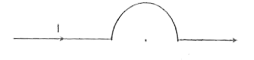
An infinitely long straight conductor is bent into the shape as shown in figure. It carries the current I and radius of the circular loop is a, then the magnetic field at the centre of the loop is ______
View SolutionA current loop, carrying a current of 5.0 A, is in the shape of a right triangle with sides 30,40, and 50 cm. The loop is in a uniform magnetic field of magnitude 80 mT whose direction is parallel to the current in the 50 cm side of the loop. Find the magnitude of (a) the magnetic dipole moment of the loop and (b) the torque on the loop.
View Solution
Knowledge Check
Magnetic induction at the center of a circular loop carrying a current is 'B' . If 'A' is the area of the coil, the magnetic dipole moment of the loop is
ABA2μ0πBBA(√A)μ0CBA(√A)μ0πDBAμ0√AπA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
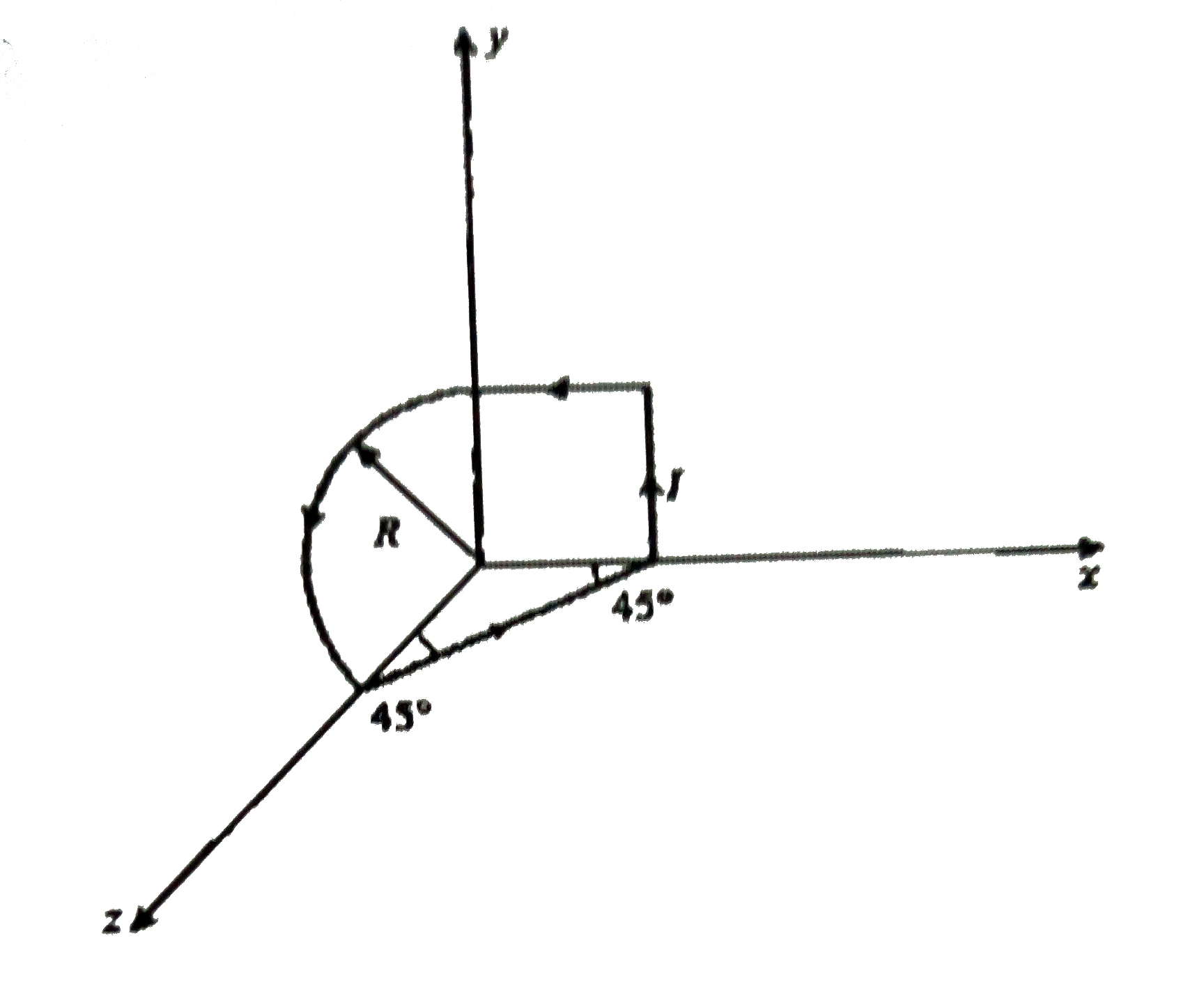
Find the magnetic moment of the current carrying loop shown in figure.
View SolutionHow will the conductor, carrying current I0 rotate immediately after it is released in following three cases [consider magnetic force only]
(a) Conductor carrying current I0 is placed symmetrically above poles of a fixed U shaped magnet (figure a).
(b) Conductor carrying current I0 is placed symmetrically at a distance from a fixed current (I1) carrying wire (fig. (b))
(c) An insulated circular current carrying wire is held fixed in vertical plane. Conductor carrying current I0 is in the shape of a circle of diameter nearly equal to that of the fixed insulated circle. The planes of the two circles are perpendicular to each other (fig. (c)) with xy as common diameter


View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View SolutionWhat is the magnetic moment of a current carrying thin circular loop if the radius of the loop is equal to R and the magnetic induction at its centre is equal to B ?
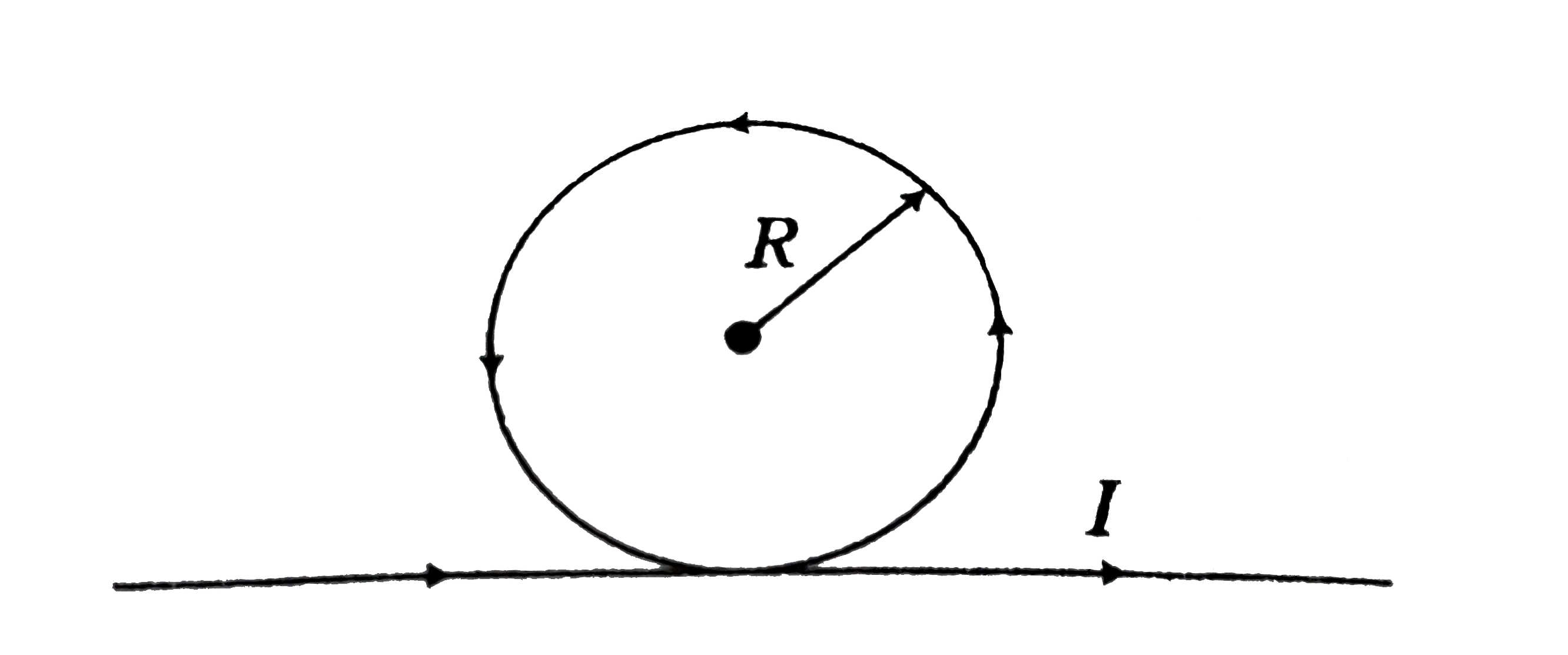
View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R meter. The magnetic induction at the centre of loop is
View Solution