Consider the uniform magnetic field shown:

Starting from point P and without leaving the region of magnetic field, is it possible to choose a closed path (that is, a path that returns to P) for which the line integral of the magnetic field is nonzero?
A
Yes, but only anti clockwise
B
Yes, but only clockwise
C
Yes, both anti clockwise and clockwise
D
No
Video Solution
Text Solution
The correct Answer is:D
Any path can be broken into small horizontal and vertical segments. Because the magnetic field is horizontal only be horizontal segments contribute to the line integral. Moving away from P and then returning to it, involves as many horizontal segments to the left as horizontal segments to the right and so the net contribution is always zero.
|
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-VI (SINGLE ANSWER QUESTION)
81 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level =I (H.W)
42 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT Based Questions
20 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
Knowledge Check
The lines of force of uniform magnetic field
Amust be convergentBmust be divergentCmust be parallel to each otherDintersectThe magnetic field is zero at mid point of AB and at P as shown
 AThe current is equal in both wires and insideBThe magnetic field of M in upwardCThe magnetic field is maximum at x=±a2DAll options are correct
AThe current is equal in both wires and insideBThe magnetic field of M in upwardCThe magnetic field is maximum at x=±a2DAll options are correctStatement-1: Magnetic field lines cannot start from a point nor end at a point.
Statement-2: The line integral of magnetic field induction over a closed path is not zero.AStatement-1 is true, Statement-2 is true, Statement-2 is a correct explanation of Statement-1.BStatement-1 is true, Statement-2 is true, Statement-2 is not correct explanation of Statement-1.CStatement-1 is true, Statement -2 is false.DStatement-1 is false, Statement -2 is true.
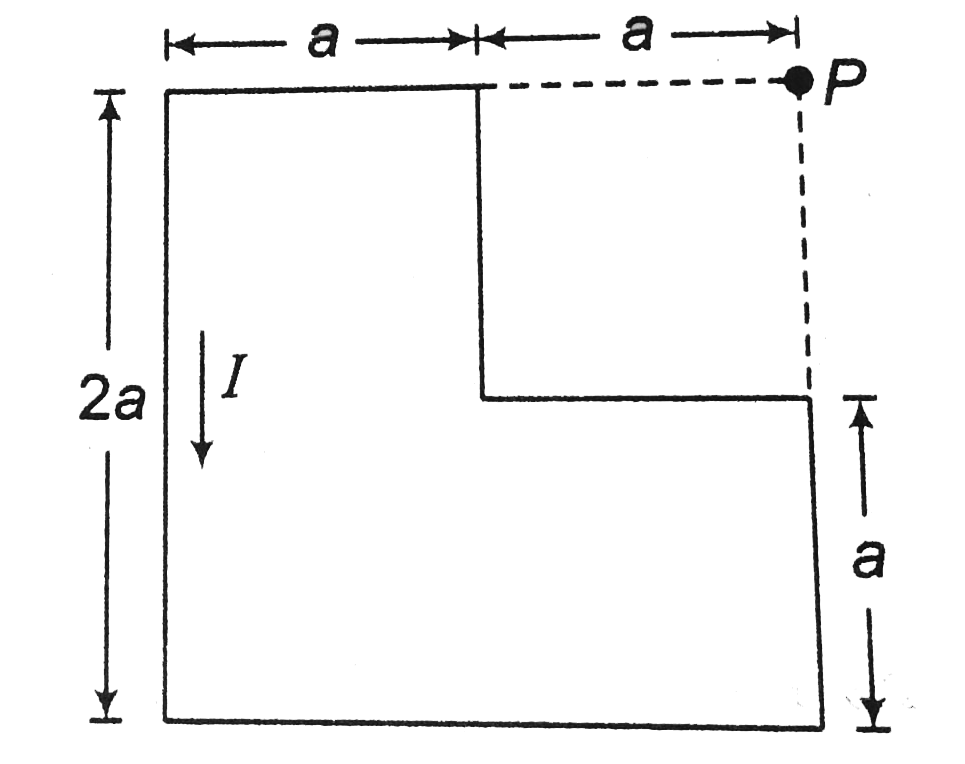
Find the magnetic field at P due to the arrangement shown.:

View SolutionFind the magnetic field at P due to the arrangement shown
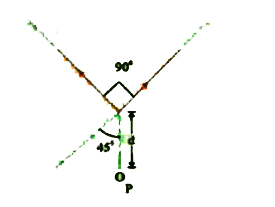
View SolutionFind the magnetic field at point P in following cases
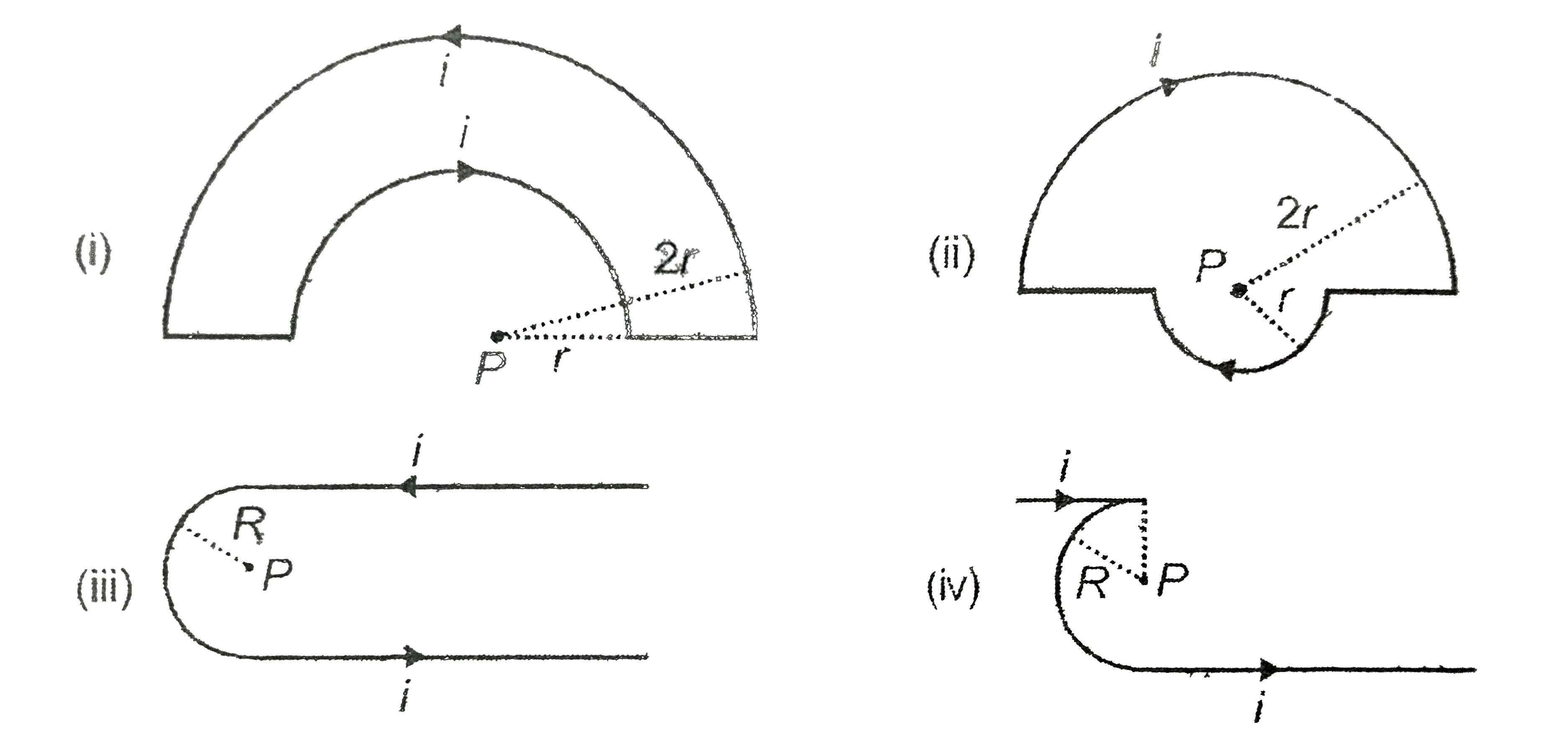
View SolutionFind the magnetic field at P due to the arrangement shown
 .
.
View SolutionThe magnetic field at P in the arrangement shown is
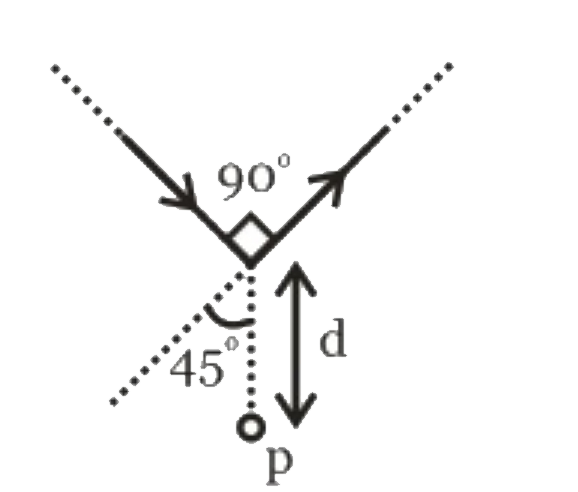
View Solution