A long cylidrical conductor of radius R carries a current i as shown in figure. The current desity J is a function of radius according to J=br, where b is a constant. Find an expression for the magnetic field B

a. at a distasnce r1<R and
b.at a distance r2>R, measured from the axis.

(a) r1<R
Consider a circle of radius r and thickness dr
dA=2πrdr
di1=jdA=2cr.2πrdr
Current inside circle of radius r1(r1<R)
i1=4πc∫r10r2dr=4πcr313
B.2πr1=μ0i1=4πcr31μ03
B=2cr21μ03
(b) r2>R
Current inside circle of raduis r2, current exists only in circle of radius R
i2=4πc∫R0r2dr=4πcR33
B.2πr2=μ0i2=μ0.4πcR33
B=2cR3μ03r2
Topper's Solved these Questions
Similar Questions
A long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis
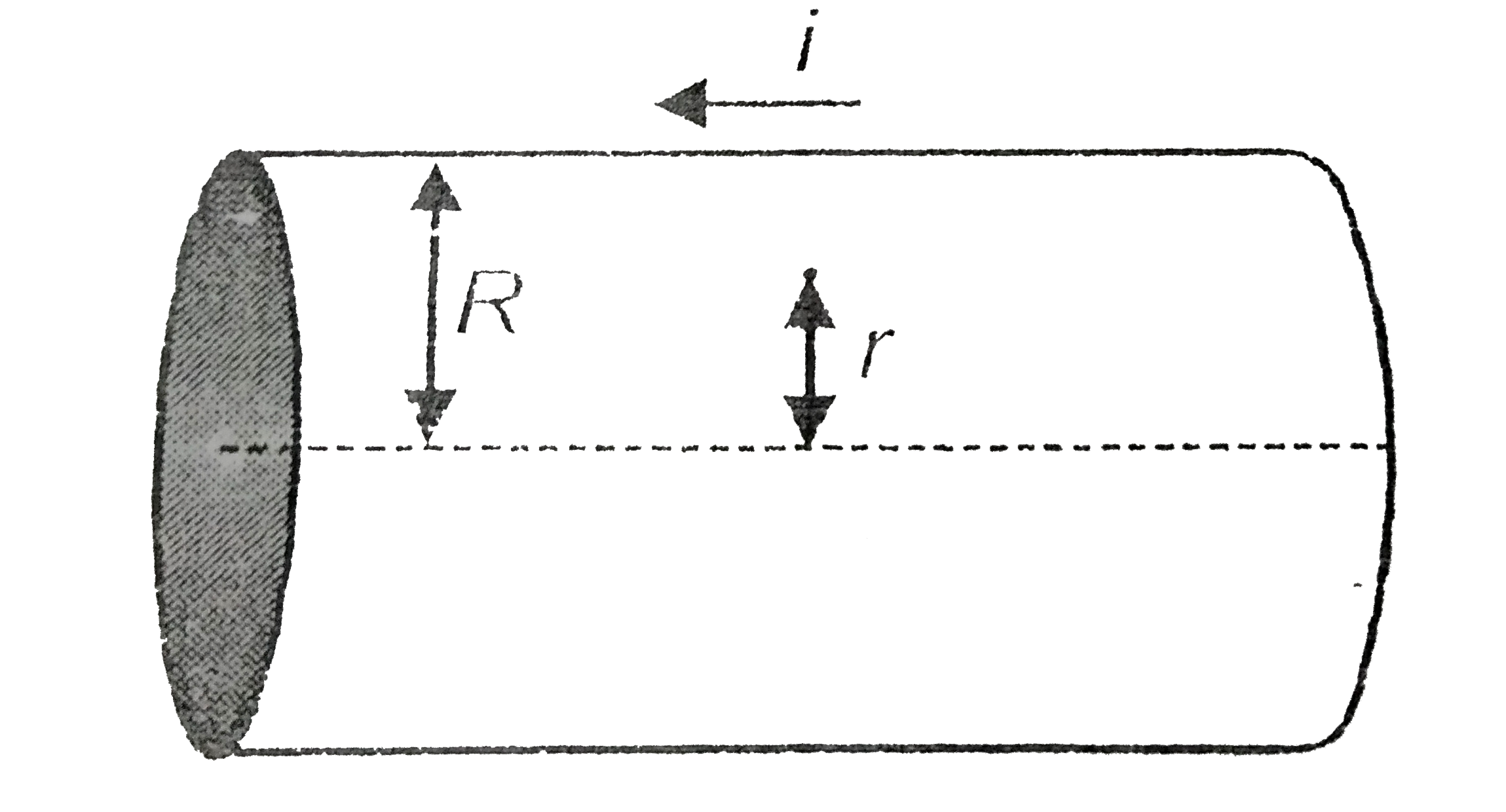
View SolutionA solid cylindrical conductor of radius R carries a current along its length.The current density J1 however, is not unifrom over the cross section of the conductor but is a function of the radius according to J=br, where b is a constant.the magnetic field B at r1<R is μ0br21N.Then find value of N
View Solution
Knowledge Check
A long cylindrical conductor of radius R carries I as shown. The current density is a function of radius r as j = br, where b is a constant. The magnetic field at a distance r1(r1<R) is
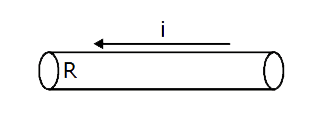 Aμ0br212Bμ0br312Cμ0br213Dzero
Aμ0br212Bμ0br312Cμ0br213DzeroConsider an infinite long cylinderical conductor of radius R carrying a current I with a non uniform current density J=αr where a is a constant. Find the magnetic field for inside and outside prints.
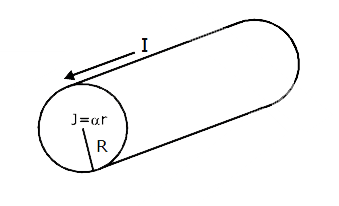 AInside αu03r2BOutside αu03Rr3Cinside the outer conductor αμ03R2DOutside αμ03rR3
AInside αu03r2BOutside αu03Rr3Cinside the outer conductor αμ03R2DOutside αμ03rR3A long copper tube of inner radius R carriers a current i. The magnetic field B inside the tube is
Aμ0i2πRBμ0i4πRCμ0i2RDZero
A circular loop of radius R carries a current I. Obtain an expression for the magnetic field at a point on its axis at a distance x from its centre.
View SolutionSuppose that the current density in a wife of radius a varies with r according to J=Kr2, where K is a constant and r is the distance from the axis of the wire. Find the megnetic field at a point distance r from the axis when (a) r < a and (b) r > a

View SolutionA non-homogeneous cylinder of radius "R" carries a current I whose current density varies with the radial "distance "r" from the centre of the rod as J=σr where σ is a constant.The magnetic field at a point "P" at a distance r<R from the centre of the rod is
View SolutionSuppose that the current density in a wire of radius a varius with r according to Kr2 where K is a constant and r is the distance from the axis of the wire. Find the magnetic field at a point at distance r form the axis when (a) rlta and (b) rgta.
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View Solution
