A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point (a) just inside the tube (b) just outside the tube.

r<R
r<R (inside)
B=μ0ir2πR2
r=R(on the surface)
B=μ0i2πR
r>R (outside)
B=μ0i2πr
(b) 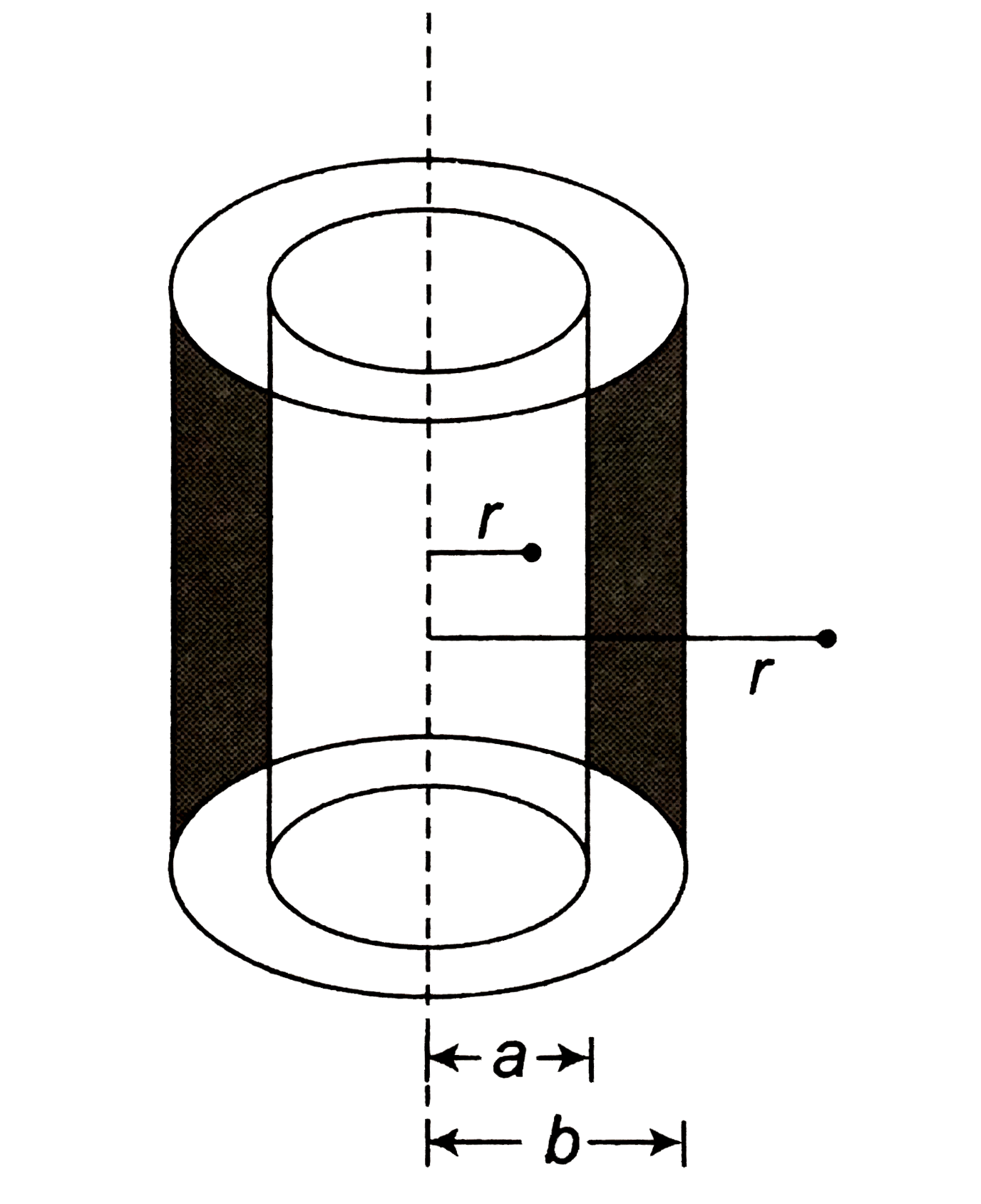
(i) Just inside the tube (r<a)
Enclosed current in circle of radius r=0,B=0
Assume this current along the axis of cylinder and apply formula of long wire
(ii) Just outside the tube (r≤b)
Enclosed current = i
B=μ0i2πr=μ0i02πb
(c) 
where r. distance from axis
(i) r<R
B=μ0ir2πR2
(ii) R<r<2R
B=μ0i2πr
(iii) 2R<r<3R
Let current in a circle of inner radius 2R and outer radius r be i1,
i1=i×π[r2−(2R)2]π[(3R)2−(2R)2]
=i(r2−4R2)5R2
Net current i−i1=i[5R2−r2+4R25R2]
=i(9R2−r2)5R2
B2πr=μ0i(9R2−r2)5R3
B=μ0i(9R2−r2)10πR2r
(iv) r>3R
Net current =0
B=0
Topper's Solved these Questions
Similar Questions
A long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View Solution
Knowledge Check
A long cylinder of wire of radius 'a' carries a current i distributed uniformly over its cross section. If the magnetic fields at distances r<aandR>a from the axis have equal magnitude, then
Aa=R+r2Ba=√ReCa=Rr/(R+r)Da=R2/rA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
Aμ0I2π(R−x)Bμ0I2πxCμ0I2π(R+x)Dnone of these
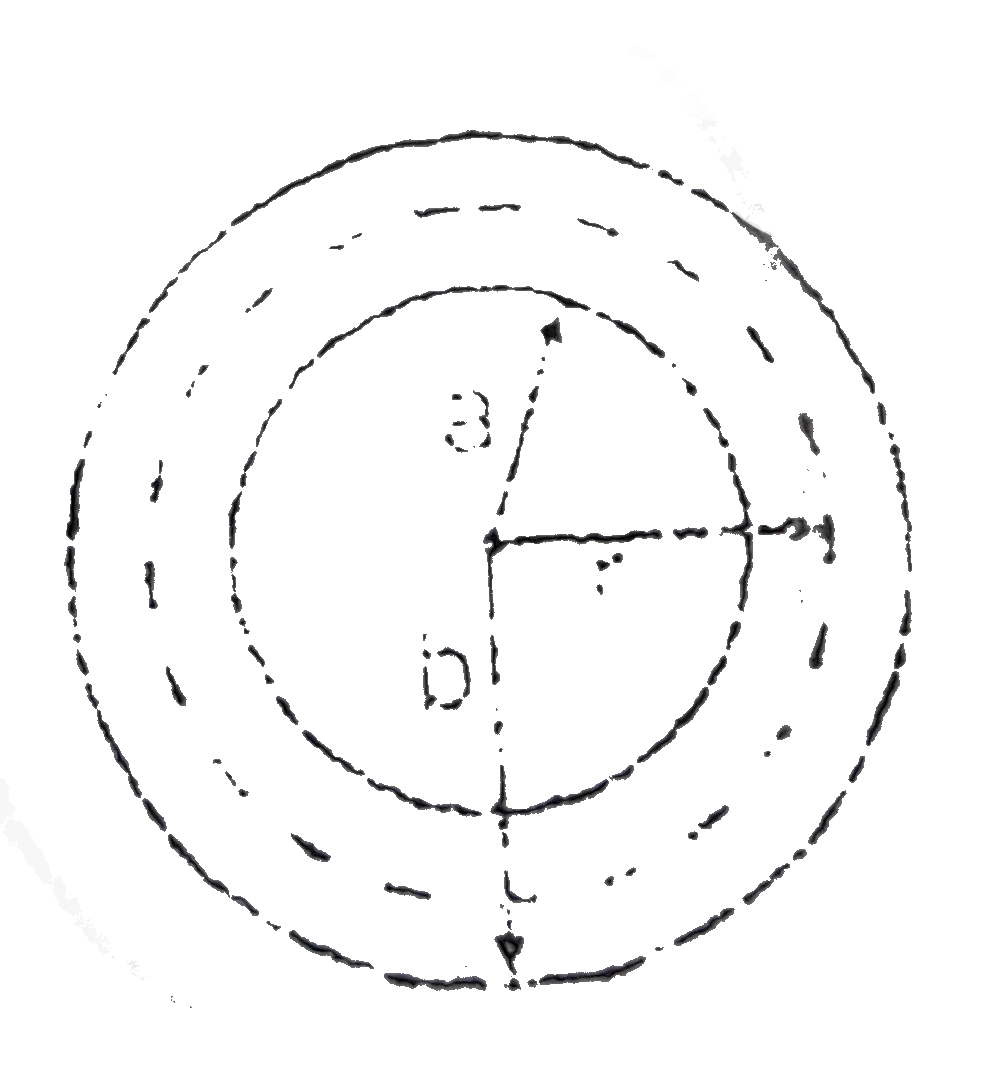
A hollow cylindrical conductor of inner radius a and outer radius b carries a current I uniformly spread over its cross-section. Find the magnetic field induction at a point inside the body of the conductor at a distance r [where a<r<b] from the axis of the cylinder.
View SolutionA thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View SolutionFigure shows a cylindrical conductor of inner radius a & outer radius b which carries a current i unifromly spread over its cross section.Show that the magnetic field B for points inside the body of the conductor (i.e. a<r<b) is given by. B=μ0i2π(b2−a2)r2−a2r.Check this formula for the limiting case of a=0.
View SolutionA long straight wire of a circular cross-section (radius r) carries a steady current I. The current is distributed uniformly across the cross-section. Calculare the magnetic field at a point (a) outside the wire , (b) inside the wire. Draw a graph showing variation of magnetic field.
View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionA hollow cylindrical conductor of radii a and b carries a current I uniformly spread over its cross-section. Prove that the magnetic field induction B for point inside the body of the conductor at a distance r from the axis of cylinder is given by, B=μ0μrI(r2−a2)2π(b2−a2)r
View Solution
