Figure shows a cylindrical conductor of inner radius a & outer radius b which carries a current i unifromly spread over its cross section.Show that the magnetic field B for points inside the body of the conductor (i.e. a<r<b) is given by. B=μ0i2π(b2−a2)r2−a2r.Check this formula for the limiting case of a=0.
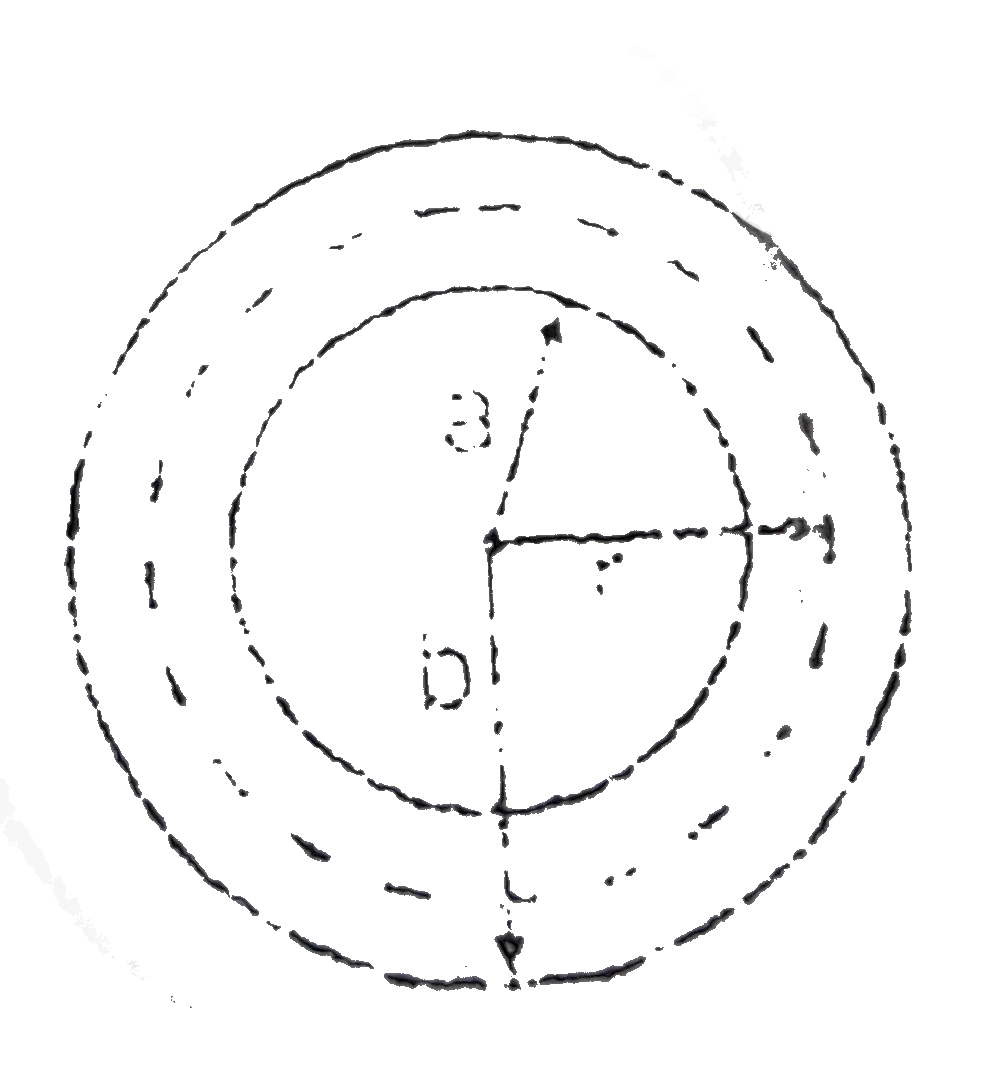
The correct Answer is:μ0ir2πb2
Step by step video, text & image solution for Figure shows a cylindrical conductor of inner radius a & outer radius b which carries a current i unifromly spread over its cross section.Show that the magnetic field B for points inside the body of the conductor (i.e. a lt r lt b) is given by. B=(mu_(0)i)/(2pi(b^(2)-a^(2)))(r^(2)-a^(2))/r.Check this formula for the limiting case of a=0. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-2
54 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-1
15 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - PROBLEM
12 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
A hollow cylindrical conductor of radii a and b carries a current I uniformly spread over its cross-section. Prove that the magnetic field induction B for point inside the body of the conductor at a distance r from the axis of cylinder is given by, B=μ0μrI(r2−a2)2π(b2−a2)r
View SolutionA hollow cylindrical conductor of inner radius a and outer radius b carries a current I uniformly spread over its cross-section. Find the magnetic field induction at a point inside the body of the conductor at a distance r [where a<r<b] from the axis of the cylinder.
View Solution
Knowledge Check
Current flows through a straight cylindrical conductor of radius r. The current is distributed uniformly over its cross-section. The magnetic field at a distanace x from the axis of the conductor has magnitude B:
AB=0 at the axisBB∝x for 0≤x≤rCB∝1/x for x>rDB is maximum for x=rA long, thick straight conductor of radius R carries current I uniformly distributed in its cross section area.The ratio of energy density of the magnetic field at distance R/2 from surface inside the conductor and outside the conductor is:
A1:16B1:1C1:4D9/16The figure shows the cross-section of a long conducting cylinder of inner radius a and outer radius b. The cylinder carries a current whose current density J=Cr2 where C is a constant. What is the magnitude of the magnetic field B at a point r, where a<r<b?
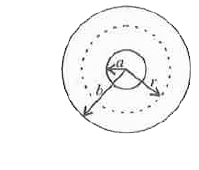 AB=μ0πC4πr2(r2−a2)BB=μ0πC4πr2(r4−a4)CB=μ0πC4π(r2−a2)DB=μ0πC4π(r4−a4)
AB=μ0πC4πr2(r2−a2)BB=μ0πC4πr2(r4−a4)CB=μ0πC4π(r2−a2)DB=μ0πC4π(r4−a4)
A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point (a) just inside the tube (b) just outside the tube.
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View Solution
