A bullet of mass 20g moving horizontally strikes a block of mass 480g suspended by a string of length 2m. If the collision is completely inelastic , the minimum velocity of bullet , so that the combined mass complete vertical circle should be
100m/s
150m/s
200m/s
250m/s
The correct Answer is:D
To solve the problem step by step, we will follow the principles of conservation of momentum and energy.
Step 1: Understand the System
We have a bullet of mass m1=20g=0.02kg moving horizontally, striking a block of mass m2=480g=0.48kg that is suspended by a string. The collision is completely inelastic, meaning the bullet and block stick together after the collision.
Step 2: Apply Conservation of Momentum
Before the collision, the block is at rest, so its initial momentum is zero. The initial momentum of the bullet is:
pinitial=m1⋅U+m2⋅0=0.02U
After the collision, the combined mass is m1+m2=0.02+0.48=0.50kg and moves with a velocity V. Thus, the final momentum is:
pfinal=(m1+m2)⋅V=0.50V
Setting the initial momentum equal to the final momentum gives:
0.02U=0.50V
From this equation, we can solve for V:
V=0.02U0.50=U25
Step 3: Determine the Minimum Velocity for Vertical Circle
To complete a vertical circle, the combined mass must have enough kinetic energy at the bottom to reach the top of the circle. At the top of the circle, the minimum velocity Vt required is given by:
Vt=√gR
where R is the radius of the circle (which is equal to the length of the string, L=2m), and g is the acceleration due to gravity (approximately 10m/s2).
Thus,
Vt=√gL=√10⋅2=√20=2√5m/s
Step 4: Set Kinetic Energy Equal to Potential Energy
The kinetic energy (KE) at the bottom must equal the potential energy (PE) at the top:
KE=12(m1+m2)V2
PE=(m1+m2)g(2L)=(0.50)(10)(4)=20J
Setting KE equal to PE:
12(0.50)V2=20
Solving for V2:
0.25V2=20⟹V2=200.25=80⟹V=√80=4√5m/s
Step 5: Relate V to U
From our earlier equation V=U25:
U25=4√5
Solving for U:
U=25⋅4√5=100√5m/s
Final Step: Calculate U
Calculating U:
U≈100⋅2.236=223.6m/s
Conclusion
The minimum velocity of the bullet U required for the combined mass to complete a vertical circle is approximately:
U≈250m/s
We have a bullet of mass m1=20g=0.02kg moving horizontally, striking a block of mass m2=480g=0.48kg that is suspended by a string. The collision is completely inelastic, meaning the bullet and block stick together after the collision.
Before the collision, the block is at rest, so its initial momentum is zero. The initial momentum of the bullet is:
To complete a vertical circle, the combined mass must have enough kinetic energy at the bottom to reach the top of the circle. At the top of the circle, the minimum velocity Vt required is given by:
The kinetic energy (KE) at the bottom must equal the potential energy (PE) at the top:
PE=(m1+m2)g(2L)=(0.50)(10)(4)=20J
From our earlier equation V=U25:
Calculating U:
The minimum velocity of the bullet U required for the combined mass to complete a vertical circle is approximately:
Topper's Solved these Questions
Similar Questions
A bullet of mass m moving with velocity u on smooth surface strikes a block of mass M kept at rest. The collision is completely inelastic. Find the common velocity and the fractional loss in kinetic energy.
View SolutionA bullet of mass 10 g moving horizontally with a velocity of 400ms−1 strikes a wook block of mass 2 kg which is suspended by light inextensible string of length 5 m. As a result, the centre of gravity of the block found to rise a vertical distance of 10 cm. The speed of the bullet after it emerges out horizontally from the block will be
View Solution
Knowledge Check
A ball of mass m moving with speed v0 strikes a block of mass 3m kept at rest. The collision is completely inelastic . If k is spring constant , the maximum compression of the spring is
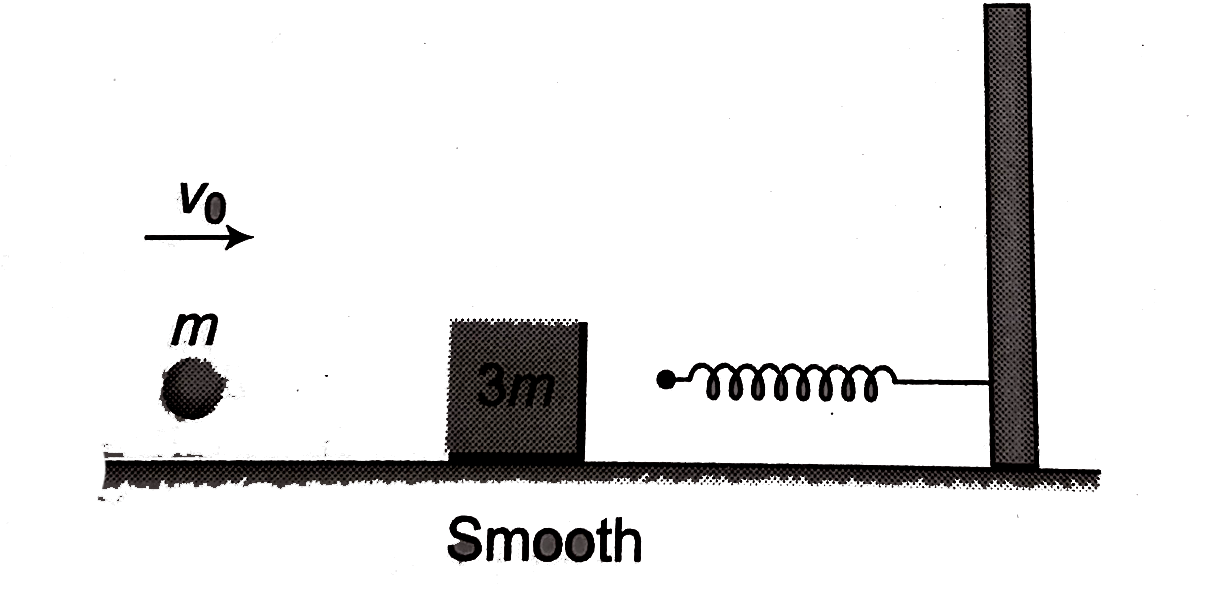 A√mv20kB√mv202kC√mv203kD√mv204k
A√mv20kB√mv202kC√mv203kD√mv204kA bullet of mass m moving with a horizontal velocity u strikes a stationary wooden block of mass M suspended by a string of length L = 50 cm. The bullet emerges out of the block with speed u4. If M = 6 m, minimum value of u so that the block can complete the vertical circle (take, g = 10 ms−2)
A10 ms−1B20 ms−1C30 ms−1D40 ms−1A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2
A bullet of mass 10 g moving horizontally with a velocity of 400ms−1 strikes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5 m. As a result, the centre of gravity of the block is found to rise a vertical distance of 10 cm. The speed of the bullet after it emerges out horizontally from the block will be
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass 10 g moving with 300m/s hits a block of ice of mass 5 kg and drops dead. The velocity of ice is
View SolutionA bullet of mass 10g moving horizontally with a velocity of 400ms−1 strikes a wooden block of mass 2kg which is suspended by a light in-extensible string of length 5m. As a result, the center of gravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out horizontally from the block will be
View Solution