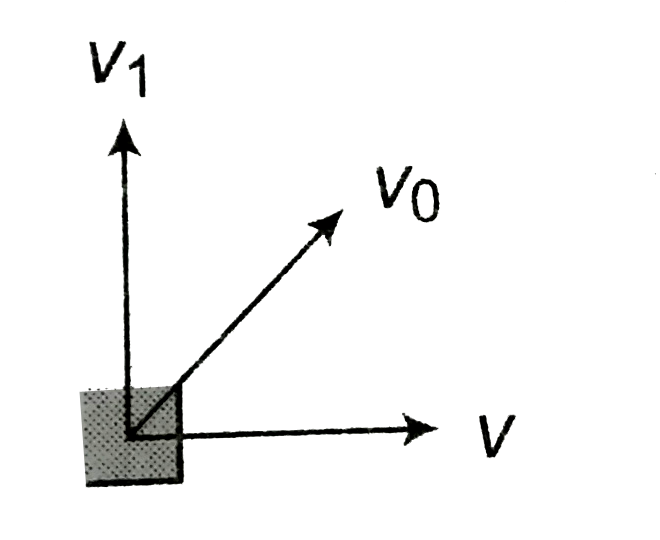
A block of mass is placed on smooth surface. Another block of mass is given velocity in horizontal direction , as shown. Find the speed of when it breaks off from . Also , calculate the maximum height attained by it from its initial level. Take .

Applying the momentum and energy conservation
Speed of , when it breaks off
Now the block of mass will move as a free particle on a parabolic path.
The maximum height attained by the smaller block from its initial level is


Topper's Solved these Questions
Similar Questions
Knowledge Check
A block of mass m is released from a height R on the frictionless incline as shown. The incline leads to a circle of radius R/2. The maximum height attained by the block is
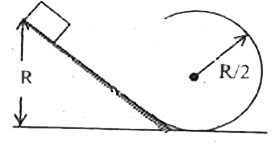 Aless than R/2Bgreater than RCequal to RDless than R but greater than R/2
Aless than R/2Bgreater than RCequal to RDless than R but greater than R/2A block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isAμgBμMmgCμmMgDgμA block of mass 2 m is pulled along a horizontal frictionless surface by a rope of mass m as shown in the figure given. What force is exerted by the rope on the block ?
 AF3BF2C2F3DF
AF3BF2C2F3DF
A block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
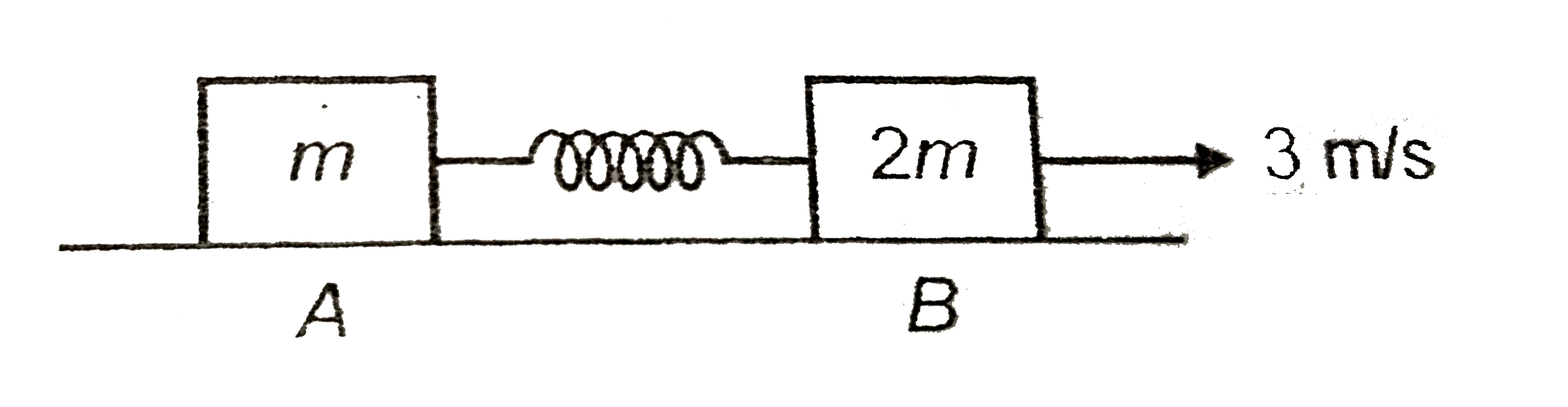
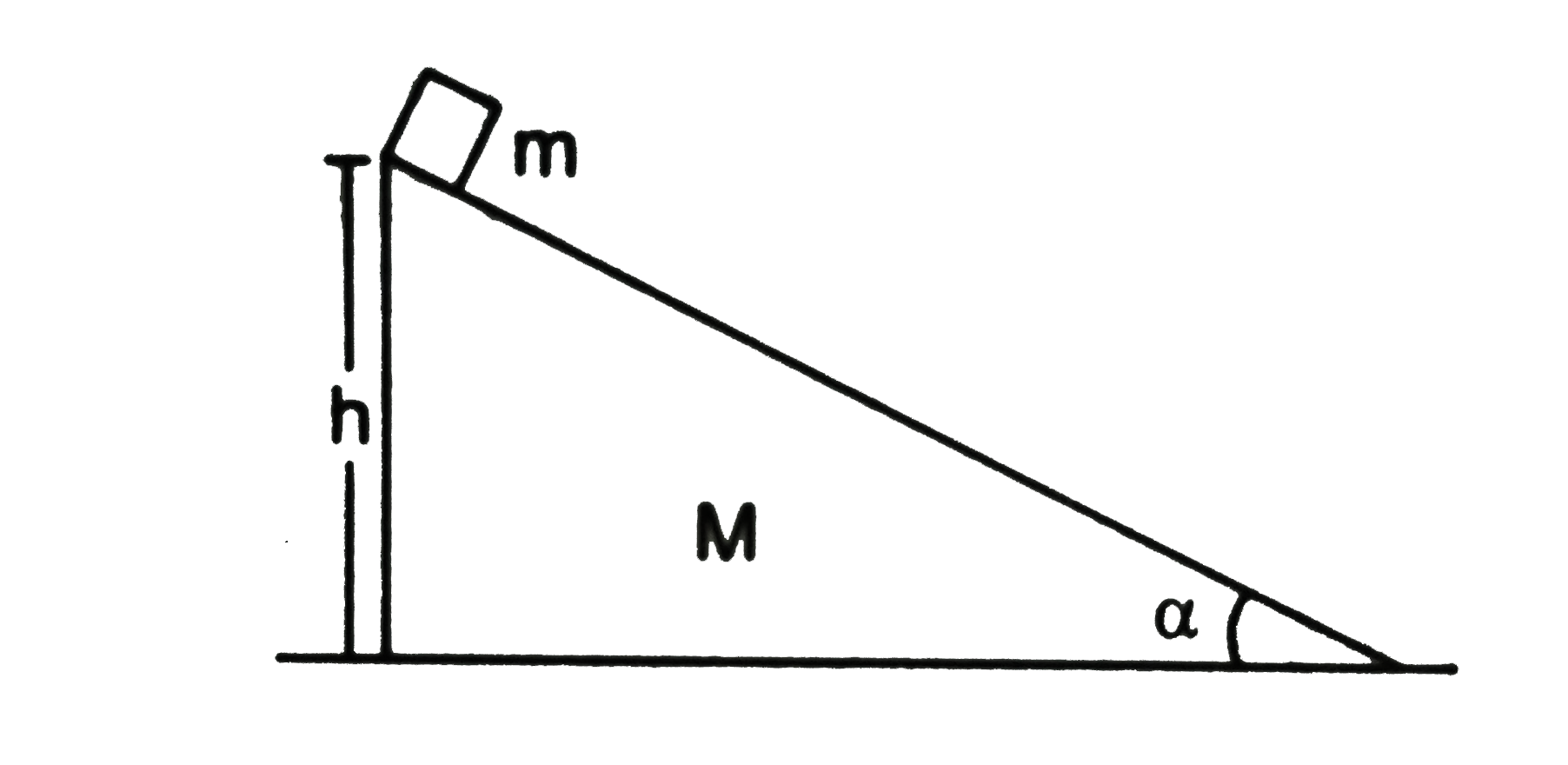
View SolutionA block of mas m is placed on a triangular block of mas m, which in tunis placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
View SolutionA block of mass m is relesed from rest from a height h onto a smooth sledge of mass M fitted with an ideal spring of stiffness k.

View SolutionAll surfaces shown in figure are smooth. Wedges of mass 'M' is free to move. Block of mass 'm' is given a horizontal velocity v0 as shown. Find the maximum height 'h' attained by 'm' (over the wedges or outside it).

View Solution

