A boy of mass m is riding on a trolley of mass M which is moving on smooth floor at speed v0. He jumps off in the opposite direction of motion of trolley with velocity u relative to the trolley before the jump. Find the velocity of the trolley after jump.
To solve the problem, we will use the principle of conservation of momentum. Here are the steps to find the velocity of the trolley after the boy jumps off:
Step 1: Understand the Initial Conditions
Initially, both the boy and the trolley are moving together with a velocity v0. The total mass of the system is M+m, where M is the mass of the trolley and m is the mass of the boy.
Step 2: Define the Final Conditions
After the boy jumps off the trolley, he jumps in the opposite direction of the trolley's motion with a velocity u relative to the trolley. We need to find the final velocity V of the trolley after the boy jumps.
Step 3: Express the Boy's Velocity
The velocity of the boy with respect to the ground after he jumps can be expressed as:
vboy=v0−u
This is because the boy jumps in the opposite direction to the trolley's motion.
Step 4: Apply Conservation of Momentum
According to the conservation of momentum:
Initial Momentum=Final Momentum
The initial momentum of the system (before the jump) is:
Pinitial=(M+m)v0
The final momentum of the system (after the jump) is:
Pfinal=m(v0−u)+MV
where V is the final velocity of the trolley.
Step 5: Set Up the Equation
Setting the initial momentum equal to the final momentum gives us:
(M+m)v0=m(v0−u)+MV
Step 6: Rearrange the Equation
Rearranging the equation to solve for V:
Mv0+mv0=m(v0−u)+MV
Mv0+mv0=mv0−mu+MV
Mv0+mu=MV
V=Mv0+muM
Step 7: Final Result
Thus, the final velocity of the trolley after the boy jumps off is:
V=Mv0+muM
Initially, both the boy and the trolley are moving together with a velocity v0. The total mass of the system is M+m, where M is the mass of the trolley and m is the mass of the boy.
After the boy jumps off the trolley, he jumps in the opposite direction of the trolley's motion with a velocity u relative to the trolley. We need to find the final velocity V of the trolley after the boy jumps.
The velocity of the boy with respect to the ground after he jumps can be expressed as:
vboy=v0−u
This is because the boy jumps in the opposite direction to the trolley's motion.
According to the conservation of momentum:
Initial Momentum=Final Momentum
The initial momentum of the system (before the jump) is:
Pinitial=(M+m)v0
The final momentum of the system (after the jump) is:
Pfinal=m(v0−u)+MV
where V is the final velocity of the trolley.
Setting the initial momentum equal to the final momentum gives us:
(M+m)v0=m(v0−u)+MV
Rearranging the equation to solve for V:
Mv0+mv0=m(v0−u)+MV
Mv0+mv0=mv0−mu+MV
Mv0+mu=MV
V=Mv0+muM
Thus, the final velocity of the trolley after the boy jumps off is:
V=Mv0+muM
Topper's Solved these Questions
Similar Questions
Two boys each of mass 40kg are standing on the right side of a trolley of mass 80kg , initially at rest on smooth floor. The boys jumps to the right with velocity 3m/s with respect to the trolley before the jump. Find the final velocity of the trolley if the jumps : (a) together , (b) one after the other and (c ) one boy is on the left and the other on the right , the boy on the left jumps to the left and then the boy on the right jumps to the right. Each boy jumps with 3m/s with respect to the trolley before the jump.
View SolutionA flat car of mass M with a child of mass m is moving with a velocity v1. The child jumps in the direction of motion of car with a velocity u with respect to the car. Find the final velocities of the child and that of the car after jump.
View SolutionA boy of mass 60kg running at 3/s jumps on to a trolley of mass 140kg moving with a velocity of 1.5m/s in the same direction . What is their common velocity?
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
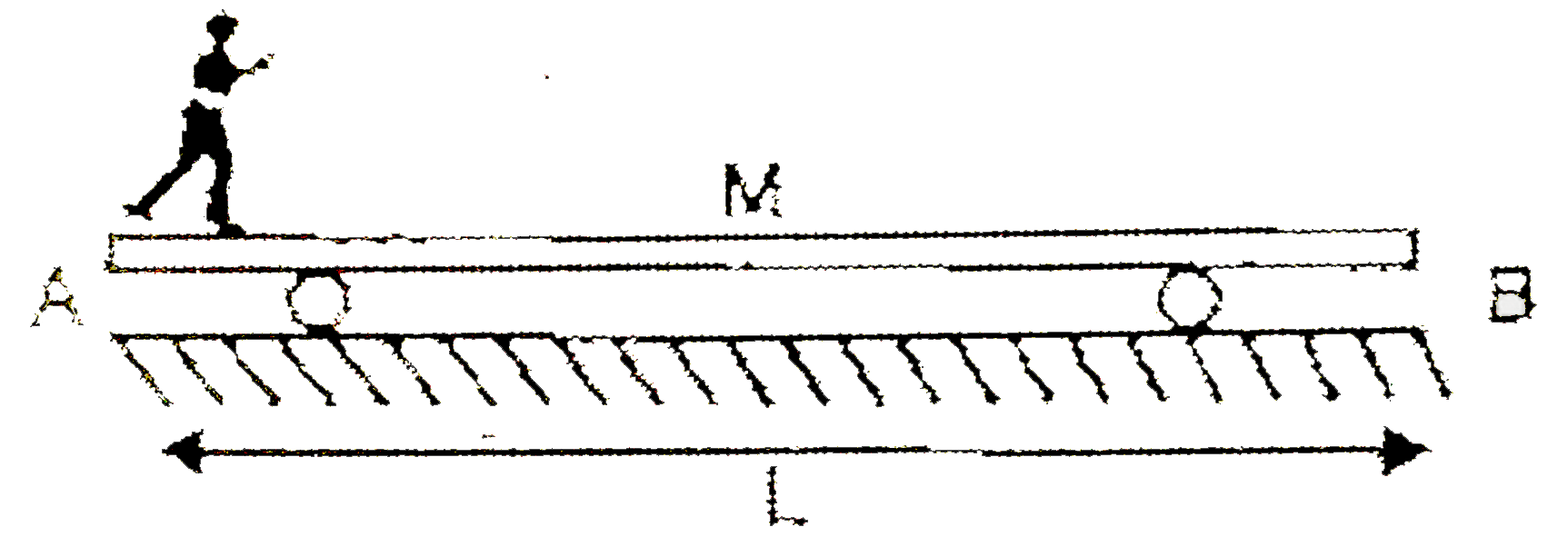
The velocity of the man with respect to ground v1 will be:
View Solutiona. A rail road flat car of mass M can roll without friction along a straight horizontal track . Initially, a man of mass m is standing on the car which is moving to the right with speed v0. What is the change in velocity of the car if the man runs to the left so that his speed relative to the car is vrel just before he jumps off at the left end?
b. If there are n men each of mass m on the car, should they all run and jump off together or should they run and jump one by one in order to give a greater velocity to the car?

View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
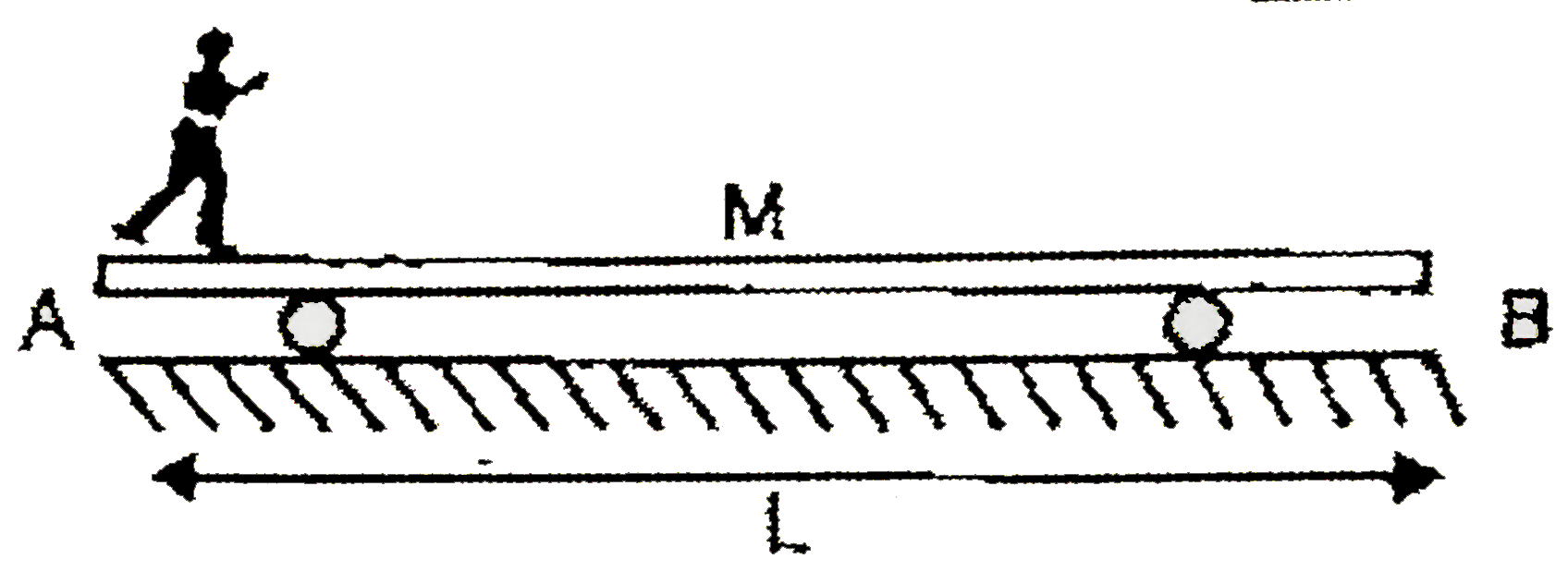
As the man walks on the trolley, the centre of mass of the system (man+ trolley) :
View SolutionThis figure shows a man of mass m standing at the end A to a trolley of mass M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.

(a) Find the time taken by the man to reach the other end.
(b) As the man walk on the trolley, find the velocity centre of mass of the system (man+trolley).
(c) When the man reaches the end B, find the distance moves by the trolley with respect to ground.
(d) Find the distance moved by the man with respect to ground.
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
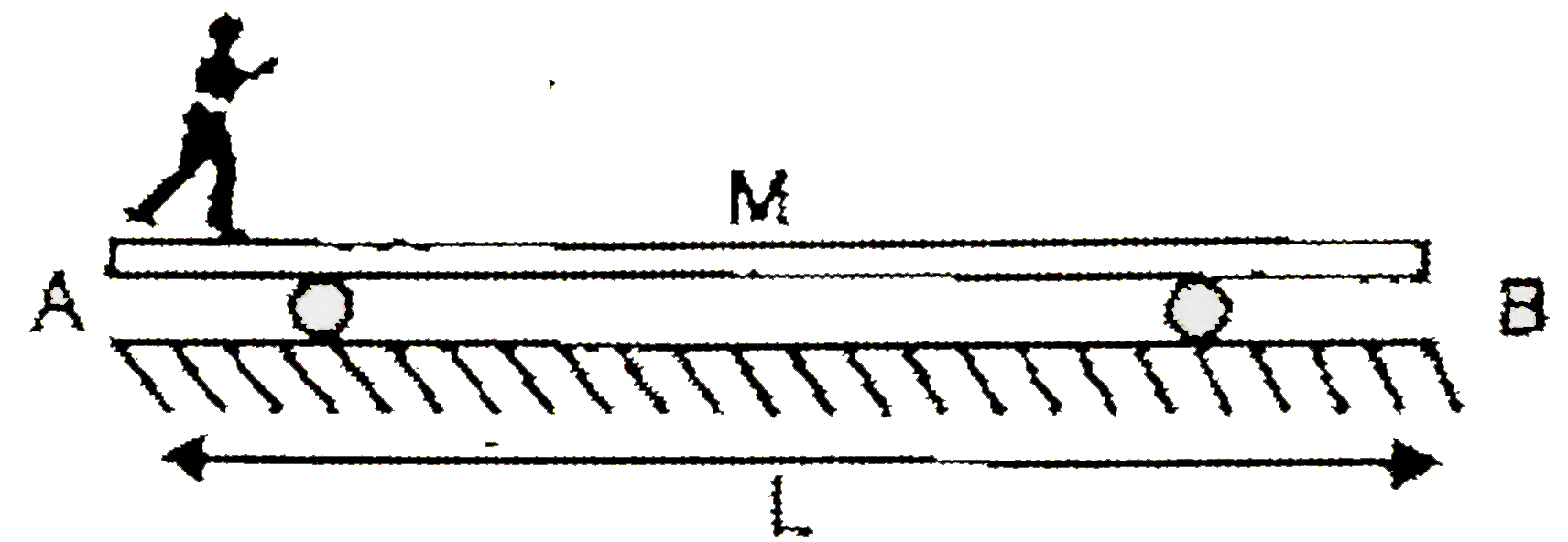
When the man starts moving, then the velocity of the trolley v2 with respect to ground will be:
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.

When the man reaches the end B, the distance moves . by the trolley with respect to ground is:
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
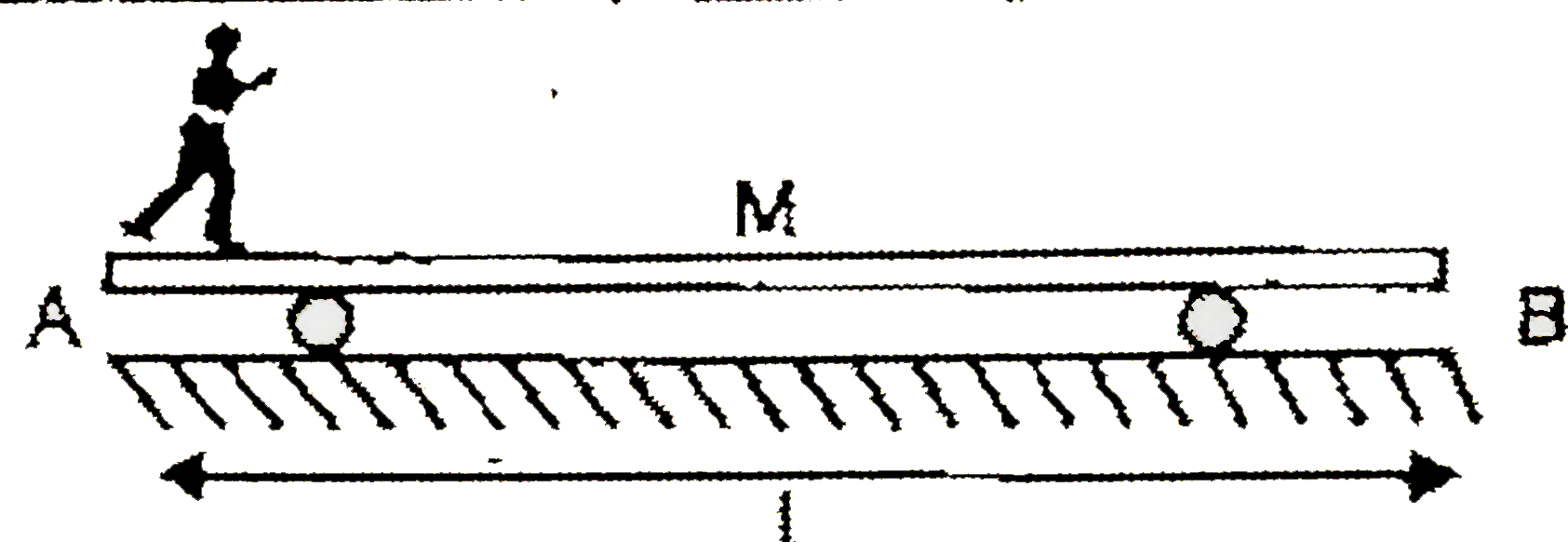
The time taken by the man to reach the other end is:
View Solution
