Cylinder
Cylinder
In Mathematics, a cylinder is one of the basic geometrical shapes. It has two parallel circular bases at a distance which is also called as the height of the cylinder. One of the real-life examples is the LPG cylinder. Having a three-dimensional shape, it has volume and surface area. Coming to the total area of cylinder, it is equal to the sum of its curved surface area and area of the two circular bases.
Here we will discuss the formulas, definitions, surface area of a cylinder, properties of the cylinder, the volume of a cylinder, and so on. Some examples will be provided that would consist of questions and answers so that students can benefit a lot out of it.
What is the definition of a Cylinder?
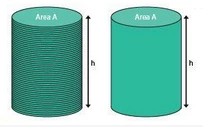
A cylinder is a three-dimensional solid which is joined by a curved surface and holds two parallel bases at a fixed distance. The bases are normally found to be circular in shape where a line segment joins the centre of the two bases, and this is known as the axis of the cylinder. The height is the perpendicular distance between the bases, ‘b’ and the radius, ‘r’ is the distance from the axis to the outer surface of the cylinder.
Cylinder Formulas
There are three major quantities of the cylinder on the basis of which we have the formulas.
- Volume
- Lateral Surface Area or curved surface area
- Total Surface Area
Moving forward, we will have a look at the formulas,
Volume: Space which is occupied in any three-dimensional plans is the volume of the cylinder. The volume is described as the amount of water that could be immersed in a cylinder. Now, here is the formula for the volume as below:
The volume of the Cylinder, V = πr2h cubic units
Here, h = height and r = radiu
Curved Surface Area: This is the area which is contained between the two parallel circular bases. The curved surface area is also known as a lateral surface area. Now, coming to its formula, here it goes:
Curved Surface Area = 2πrh square units
Total Surface Area: The sum of the area of the two circular bases and the curved surface is known as total surface area.
TSA = Curved surface + Area of Circular bases
TSA = 2πrh + 2πr2
Here we can find that 2πr is common in the above expression. Therefore,
Total surface area, A = 2πr (r + h) square units
Related Video:
- Volume of a Cylinder
- Right Circular hollow cylinder
- Right Circular Cylinder
- Cylinder: volume: CSA: TSA
- Volume and surface area of cylinder
Properties of Cylinder
Here, we will look at the properties of the cylinder
- When it comes to the bases, they are always parallel and congruent.
- It proves to be a “Right Cylinder” if a right angle is formed by the axis with the bases.
- It has the identical cross-section and so is considered to be similar to the prism.
- It is said to be an “Oblique Cylinder” if the bases are not exactly over each other but sideways. In this case, the right angle is not produced by the axis.
- It is called a “right circular cylinder” if the shape of the bases is circular.
- It is termed as an “Elliptical Cylinder” if the bases are in an elliptical shape.
Problems and solutions of Cylinder
Question 1: The radius of the cylinder is 7 cm, and the height is 10 cm.
Solution: From the formula, we know that
Total surface area of a cylinder, A = 2πr(r + h) square units
Therefore, A = 2π × 7(7 + 10) = 2π × 7(17) = 2π × 119 = 238 × 3.14 = 747 cm2
Question 2: A cylindrical shape water container has the height of 7cm and a diameter of 14 cm. Can you find the volume?
Solution: Given,
Diameter of the container = 14 cm
Thus, the radius of the container = 14/2 = 7cm
Height of the container = 7cm
As we know, from the formula,
Volume of cylinder = πr2h cubic units.
Therefore, the volume of the given container, V = π × 72 × 7
V = π × 49 × 7 = (22/7) × 49 × 7 = 22 × 49
V = 1078 cm3
Question 3: Calculate the volume of a cylinder where the area of the base is 30 cm 2 and the height is 6 cm.
Solution: Here,
Base = 30 cm2
Height = 6 cm
V = Area of base x height
= 30 cm2 x 6 cm
= 180 cm3
Therefore the volume of the cylinder in 180 cm3
Question 4: Calculate the volume of a cylinder where the radius of the base is 14 cm, and the height is 10 cm.
Solution: Here,
Radius of the base = 14 cm
Height = 10 cm
V = Area of base x height
= πr2h
= 22/7 x 142 x 10 (we have taken π as 22/7)
= 6,160 cm3
Therefore the volume of the cylinder in 6,160 cm3
Important Chapters:

Question 4: Calculate the volume of a cylinder where the radius of the base is 14 cm, and the height is 10 cm.
Similar Questions
As shown in the adjacent figure, a sphere is placed in a cylinder. It touches the top, bottom and the curved surface of the cylinder. If radius of the base of the cylinder is 'r',
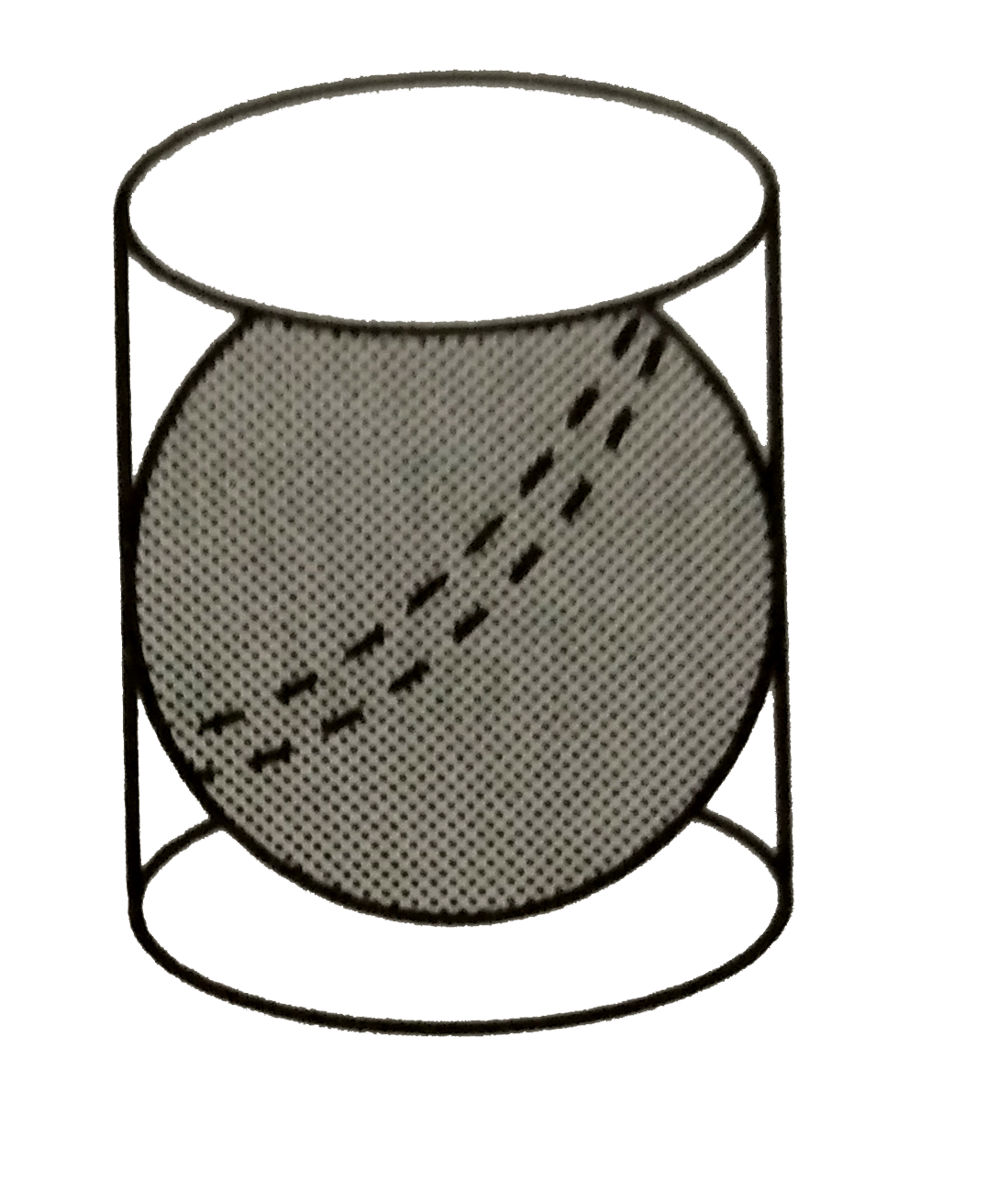
(i) what is ratio of the radii of the sphere and the cylinder?
(ii)what is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
(iii) what is the ratio of the volumes of the cylinder and the sphere?
View SolutionThree spheres of radius 'r ' are kept inside a cylinder such that two of the spheres are at bottom touching each other and sides of the cylinder while the third sphere is touching the two bottom spheres and the top of the cylinder. Then the volume of the cylinder is :
View Solution
Knowledge Check
The axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v1. It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I

For the entire process the quantitiy (ies) which will remain conserved for the (cylinder+block) system is/ are (anuglar momentum is considered about the cylinder axis)Amechanical energy, momentum and angular momentumBmechanical energy & angular momentum onlyCmomentum & angular momentum onlyDangular momentum onlyA small cylinder of2 cm diamete r is connected to a large cylinder of 20 cm di ameter and each cylinder is fitted with suitable pistons. An incompressibl e fluid is fi lled in the cylinders. If a force of 60 N is appl ied to the piston of the small cylinder, then the force exerted on the p iston of the large cylinder will be
A600 NB6000 NC12000 ND1200 NA solid metallic right cone is melted and some solid right circular cylinders are made. If the radius of base of each cylinder is half the radius of cone and the height of each cylinder is one third the height of the cone, then the number of cylinders formed are.
A3B4C5D6
The external and the internal radii of a hollow right circular cylinder of height 15 cm are 6.75 cm and 5.25 cm respectively. If it is melted to form a solid cylinder of height half of the orignal cylinder, then the radius of the solid cylinder is-
View SolutionAn iron cylinder contains helium at a pressure of 250 K Pa at 300 K. Then room in which cylinder is placed catches fire. Predict whether the cylinder will blow up before it melts or not (melting point of cylinder =1800 K)
View SolutionA cylinder of mass m is kept on an inclined plane haivng an angle of inclination 30∘. Axis of the cylinder makes an angle 30∘ with the line along the greatest slope. Assuming that cylinder rolls without slipping, the acceleration of the cylinder is
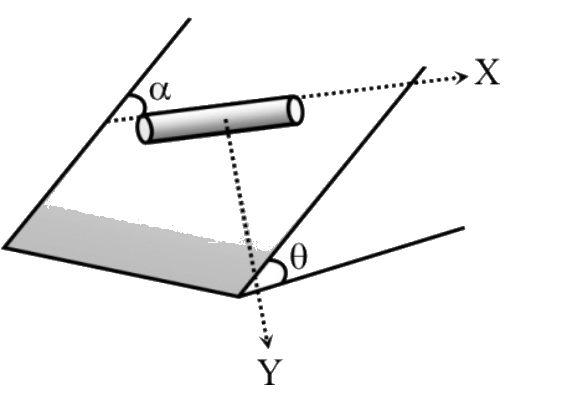
View SolutionThe hollow cylinder of length l and inner and outer radius R1 and R2 respectively. Find resistance of cylinder if current flows radially outward in the cylinder. Resistivity of material of cylinder id ρ .
View SolutionThe axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v1. It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I
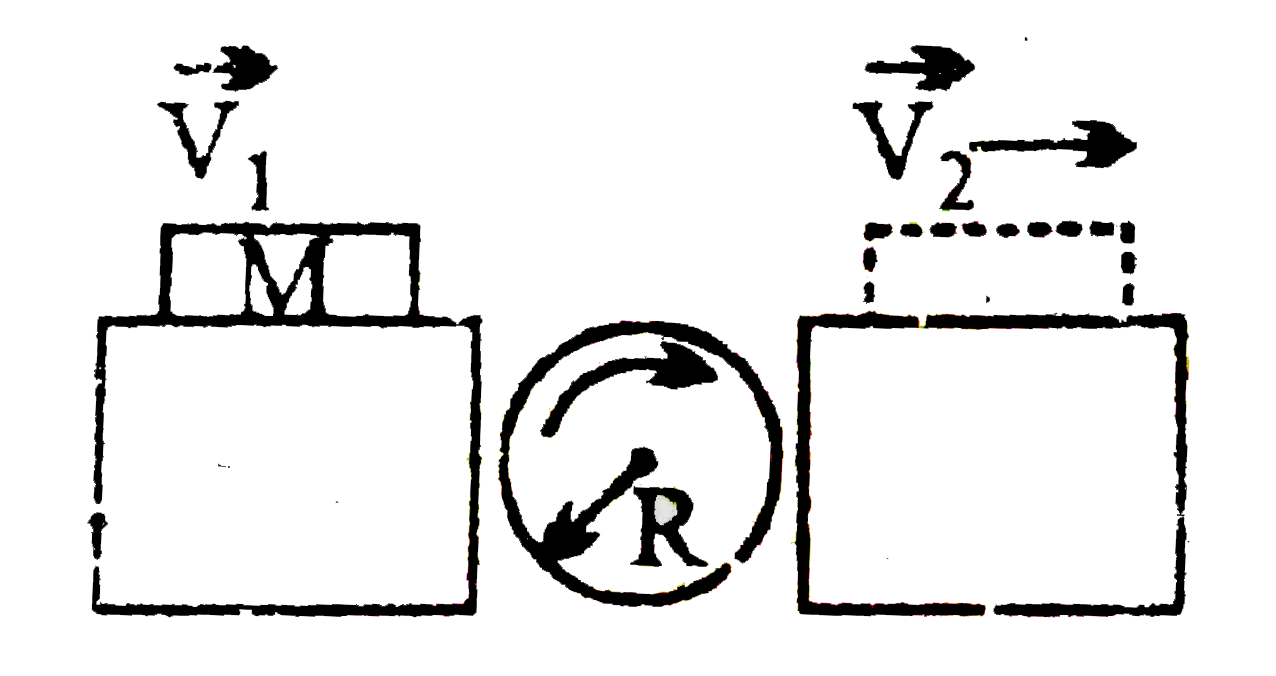
If ω is final angular velocity of the cylinder, then
View Solution