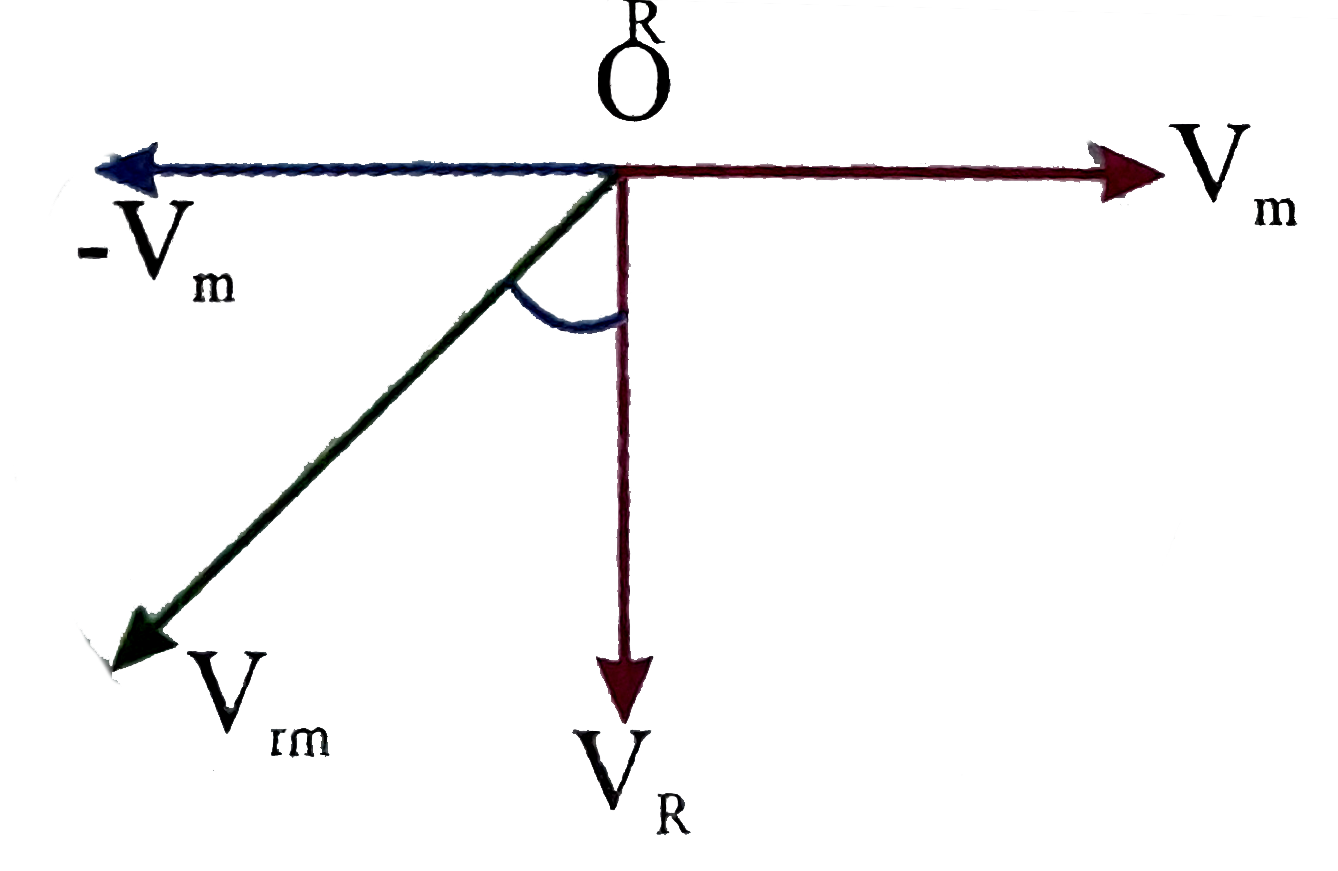
When it is raining vertically down, to a man walking on road the velocity of rain appears to be 1.5× his velocity.To protect himself from rain he should hold the umbrealla at an angle θ to vertical. The tanθ=
2√5
√52
23
32
The correct Answer is:A
→vRm=1.5vm, tanθ=vmvR
Topper's Solved these Questions
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-Vi Integer
Explore 9 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
Similar Questions
The greatest and least resultant of two forces are 7N and 3N respectively. If each of the force is increased by 3N and applied at 60∘.The magnitude of the resultant is
View SolutionThe distance between two moving particles P and Q at any time is a.If vr be their relative velocity and if u and v be the components of vr, along and perpendicular to PQ.The closest distance between P and Q and time that elapses before they arrive at their nearest distance is
View SolutionOne end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If s is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
View SolutionTwo particles move along x-axis in the same direction with uniform velocities 8m/s and 4m/s. Initially the first particle is 21 m to the left of the origin and the second one is 7 m to the right of the origin. The two particles meet from the origin at a distance of
View SolutionRain appears to fall vertically to a man walking at 3kmh^(-1) , but when he changes his speed to double, the rain appears to fall at 45^@ with vertical. Study the following statements and find which of them are correct. i. Velocity of rain is 2 (sqrt3) kmh^(-1) . ii. The angle of fall of rain (with vertical) is theta = tan^(-1)(1/(sqrt2)). iii. The angle of fall of rain (with vertical) is theta = sin^(-1) (1/(sqrt2)) . iv. Velocity of rain is 3(sqrt2)kmh^(-1) .
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA man holds his umbrella vertically up while walking due west with a constant velocity of magnitude v_(m)=1.5 m//sec in rain. To protect himself from rain, he has to rotate his umbrella through an anlge phi = 30^(@) when he stops walking. Find the velocity of the rain.
View SolutionIf a man is running on horizontal road, raise appears to him coming at 30^(@) from vertical. When he double his velocity rain appears to him coming at angle theta from vertical. Then theta is
View SolutionStatement -1 : A man standing on the ground has to hold his umbrella at an angle theta with the vertical to protect himself from rain. It is possible that the man now starts running on the ground with certain speed, but he still has to hold his umbrella at angle theta with the vertical to protect himself from rain. Statement -2 : Vertical component of velocity of rain w.r.t man does not change. if he starts running on a horizontal ground.
View SolutionA man holds his umbrella vertically upward while walking due west with a constant velocity of magnitude V_(m) = 1.5 m/sec in rain. To protect himself from rain, he has to rotate his umbrella through an angle phi = 30^(@) when he stops walking. Find the velocity of the rain.
View SolutionA person is walking in rain feels the velocity of rain as twice to his velocity. At which angle he should hold the umbrella with vertical if he moves forward, if it is raining vertically downwards
View SolutionWhen it is raining vertically down, to a man walking on road the velocity of rain appears to be 1.5 times his velocity. To protect himself from rain he should hold the umbrella at an angle θ to vertical. Then tanθ=
View SolutionA person is walking in rain feels the velocity of rain as twice to his velocity. At which angle he should hold the umbrella with vertical if he moves forward, if it is raining vertically downwards
View SolutionIt is rainning vertically downwards. By how many times that a person should increase his velocity in order to change his umbrella position from an angle 30^(@) with vertical to 60^(@) vertical to protect himself from rain.
View SolutionRain appears to fall vertically to a man walking at 3kmh^(-1) , but when he changes his speed to double, the rain appears to fall at 45^@ with vertical. Study the following statements and find which of them are correct. i. Velocity of rain is 2 (sqrt3) kmh^(-1) . ii. The angle of fall of rain (with vertical) is theta = tan^(-1)(1/(sqrt2)). iii. The angle of fall of rain (with vertical) is theta = sin^(-1) (1/(sqrt2)) . iv. Velocity of rain is 3(sqrt2)kmh^(-1) .
View Solution

