A man holds his umbrella vertically upward while walking due west with a constant velocity of magnitude m/sec in rain. To protect himself from rain, he has to rotate his umbrella through an angle when he stops walking. Find the velocity of the rain.
The correct Answer is:
To solve the problem, we need to analyze the situation involving the man, his umbrella, and the rain. We will use vector addition to find the velocity of the rain.
1. Understanding the Situation:
- The man is walking due west with a velocity Vm=1.5m/s.
- The umbrella is initially held vertically upward.
- When the man stops walking, he has to tilt his umbrella at an angle ϕ=30∘ to protect himself from the rain.
2. Setting Up the Vectors:
- Let Vr be the velocity of the rain with respect to the ground.
- The velocity of the man Vm is directed towards the west (let's assume this is the negative x-direction).
- The velocity of the rain Vr can be broken down into two components: a vertical component (downward) and a horizontal component (which we need to find).
3. Using the Angle of the Umbrella:
- When the man stops, the umbrella makes an angle of 30∘ with the vertical.
- This means that the rain appears to be coming at an angle of 30∘ from the vertical.
4. Applying Trigonometry:
- The vertical component of the rain's velocity Vry can be expressed as:
Vry=Vrcos(30∘)
- The horizontal component of the rain's velocity Vrx can be expressed as:
Vrx=Vrsin(30∘)
5. Relating the Components:
- Since the man is moving west with a velocity of 1.5m/s, when he stops, the horizontal component of the rain's velocity must equal the man's velocity:
Vrx=Vm=1.5m/s
- Therefore, we have:
Vrsin(30∘)=1.5
6. Solving for Vr:
- We know that sin(30∘)=12:
Vr⋅12=1.5
- Solving for Vr:
Vr=1.5⋅2=3m/s
7. Conclusion:
- The velocity of the rain is Vr=3m/s.
- The man is walking due west with a velocity Vm=1.5m/s.
- The umbrella is initially held vertically upward.
- When the man stops walking, he has to tilt his umbrella at an angle ϕ=30∘ to protect himself from the rain.
- Let Vr be the velocity of the rain with respect to the ground.
- The velocity of the man Vm is directed towards the west (let's assume this is the negative x-direction).
- The velocity of the rain Vr can be broken down into two components: a vertical component (downward) and a horizontal component (which we need to find).
- When the man stops, the umbrella makes an angle of 30∘ with the vertical.
- This means that the rain appears to be coming at an angle of 30∘ from the vertical.
- The vertical component of the rain's velocity Vry can be expressed as:
Vry=Vrcos(30∘)
- The horizontal component of the rain's velocity Vrx can be expressed as:
Vrx=Vrsin(30∘)
- Since the man is moving west with a velocity of 1.5m/s, when he stops, the horizontal component of the rain's velocity must equal the man's velocity:
Vrx=Vm=1.5m/s
- Therefore, we have:
Vrsin(30∘)=1.5
- We know that sin(30∘)=12:
Vr⋅12=1.5
- Solving for Vr:
Vr=1.5⋅2=3m/s
- The velocity of the rain is Vr=3m/s.
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-II & III
15 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I
45 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-I (True/False)
2 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
A man holds his umbrella vertically upward while walking due west with a constant velocity of magnitude Vm=1.5 m/sec in rain. To protect himself from rain, he has to rotate his umbrella through an angle ϕ=30∘ when he stops walking. Find the velocity of the rain.
View SolutionA man when standstill observes the rain falling vertically and when he walks at 4km/h he has to hold his umberella at an angle 53∘ from the vertical. Find velocity of the raindrops.
View Solution
Knowledge Check
When it is raining vertically down, to a man walking on road the velocity of rain appears to be 1.5× his velocity.To protect himself from rain he should hold the umbrealla at an angle θ to vertical. The tanθ=
A2√5B√52C23D32Statement -1 : A man standing on the ground has to hold his umbrella at an angle θ with the vertical to protect himself from rain. It is possible that the man now starts running on the ground with certain speed, but he still has to hold his umbrella at angle θ with the vertical to protect himself from rain.
Statement -2 : Vertical component of velocity of rain w.r.t man does not change. if he starts running on a horizontal ground.AStatement -1 is Ture, statement -2 is Ture, Statement -2 is a correct explanation for statement -1 .BStatement -1 is True, statement -2 is True, statement - 2 is NOT a correct explanation for statement -3CStatement -1 is True, Statement -2 si FalseDStatement -1 is False ,Statement -2 is True.
If a man wants to protect himselt from the rain, while moving on a road, he should hold his umbrella in the direction of……………………………………… .
View SolutionA man is walking due west with a velocity 3km/h and rain appears to be falling vertically with a velocity 4km/h. Find the velocity of rain with respect to the ground.
View SolutionA man running on a horizontal road at 6km/h finds the rain falling vertically. He doubles his speed and find that the raindrops make an angle 37∘ with the vertical. Find the velocity of rain with respect to the ground.
View SolutionA boy is running on a horizontal road with a velocity of 5 m/s. At what angle should he hold his umbrella in order to protect him self from the rain if the rain is falling vertically with a velocity of 10 m/s?
View SolutionA man is going in a topless car with a velocity of 10.8kmph."l It is raining vertically downwards.He has to hold the umbrella at angle 530 to the vertical to protect himself from rain.The actual velocity of the rain is (cos530=35)
View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.
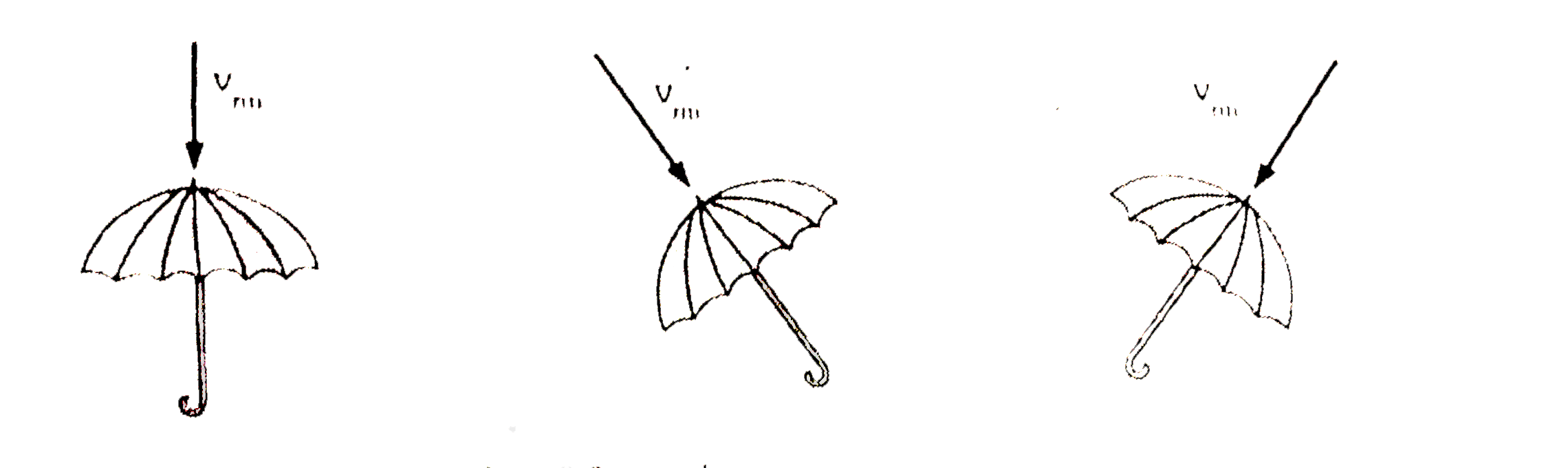
A man walks in rain at 72 cm/m due east and observes the rain falling vertically. When he stops, rain appears to strike his back at 37∘ from the vertical. Find velocity of raindrops relative to the ground.
View Solution
