A cricket fielder can throw the cricket ball with a speed v0. If he throws the ball while running with speed (u) at angle θ to the horizontal, find
(b) what will be time of flight ?
(c ) what is the distance (horizontal range) form the point of projection at which the ball will land ?
(d) find θ at which he should throw the ball that would maxmise the horizontal range range as found in (c ).
(e) how does θ for maximum range change if u>v0,u=v0,t–v0 ?
(f) how does θ in (e) compare with that for u=0 (i.e., 45^@) ?
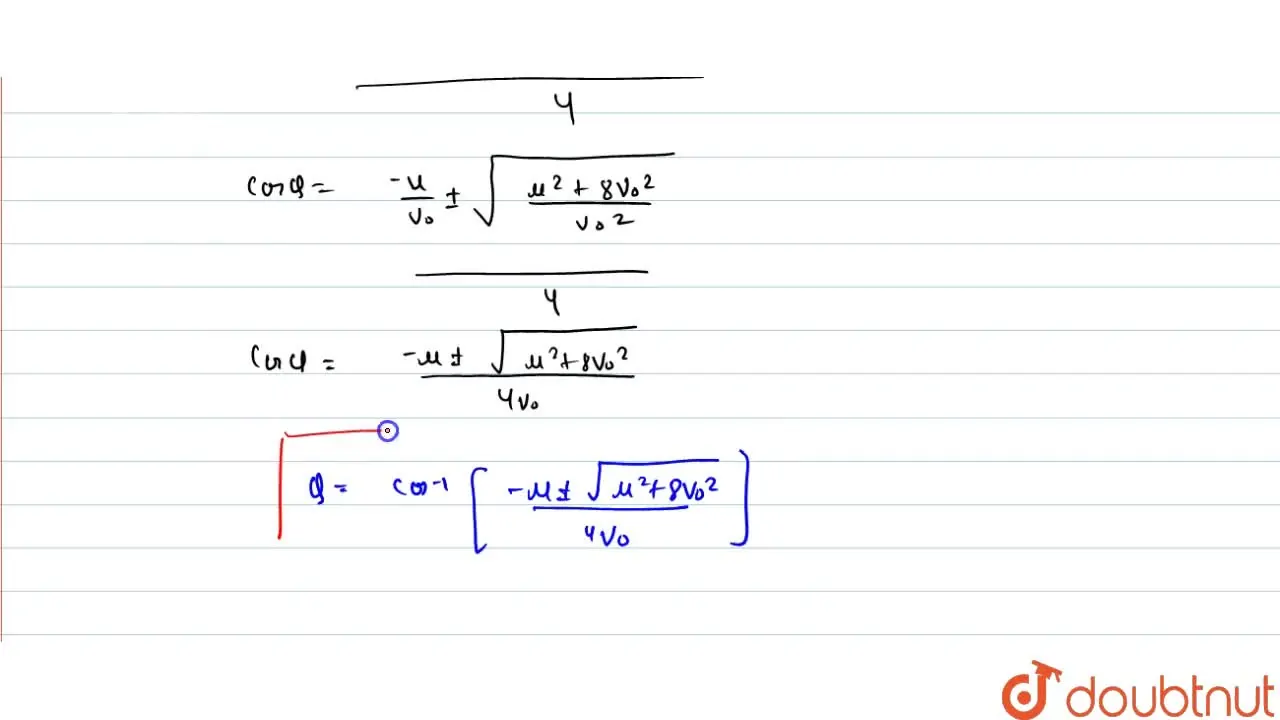
θmax=cos−1⎡⎢ ⎢⎣−u+√u2+8v204v0⎤⎥ ⎥⎦
θmax=cos−1⎡⎢ ⎢⎣u+√u2+8v204v0⎤⎥ ⎥⎦
θmax=cos−1⎡⎢ ⎢⎣−u+√u2−8v204v0⎤⎥ ⎥⎦
θmax=cos−1⎡⎢ ⎢⎣−u+√u2−4v204v0⎤⎥ ⎥⎦
The correct Answer is:A
For horiontal range to be maximum,dRdthη=0
⇒θmax=cos−1⎡⎢
⎢⎣−u+√u2+8v204v0⎤⎥
⎥⎦
Related Playlists
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Single answer31videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Multi answer18videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. MORE THAN ONE OPTION6videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
A cricket fielder can throw the cricket ball with a speed v0.If the throws the ball while running with speed u at an angle θ to the horizontal.
The effective angle to the horizontal at which the ball is projected in air as seen by a spector isView SolutionA ball is thrown at an angle θ with the horizontal. Its time of flight is 2 s. Its horizontal range is 100 m. What is the horizontal component of velocity of projection ? Take g=10ms−2.
View SolutionA particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
View SolutionA ball is thrown from the ground with velocity u at an angle θ with horizontal. If the coefficient of restitution is e , find the time of flight , the maximum height and the horizontal range after the first collision.
View SolutionA ball is projected from the ground at angle θ with the horizontal. After 1s, it is moving at angle 45∘ with the horizontal and after 2s it is moving horizontally. What is the velocity of projection of the ball ?
View SolutionA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA ball is projected with initial speed u at an angle θ above the horizontal . Calculate the time after which ball will be moving at right angle to its initial velocity.
View SolutionA ball is thrown with speed u at an angle θ with horizontally. After how much time it will move perpendicular to the initial direction of motion.
View SolutionA projectile is projected with a speed u at an angle θ with the horizontal. What is the speed when its direction of motion makes an angle θ/2 with the horizontal
View SolutionA ball moving is thrown at an angle of 60∘ with the horizontal , with initial speed of 30m/s . Calculate
(a) time of flight of the ball
(b) hrizontal range .
(c) maximum height attained .View Solution