A hiker stands on the edge of a cliff 490m above the ground and throwns a stone horiozontally with an initial speed of 15ms−1 neglecting air resistance.The speed with which it hits the ground in ms−1 is (g=9.8ms2)
9.8
99
4.9
49
The correct Answer is:B
To solve the problem of the hiker throwing a stone horizontally from a cliff, we will follow these steps:
Step 1: Determine the time taken to hit the ground
We know the height of the cliff (h) is 490 m, and the initial vertical velocity (u_y) is 0 m/s (since the stone is thrown horizontally). We can use the following kinematic equation for vertical motion:
h=uyt+12gt2
Substituting the values:
490=0⋅t+12⋅9.8⋅t2
This simplifies to:
490=4.9t2
Now, solving for t2:
t2=4904.9=100
Taking the square root:
t=10 seconds
Step 2: Calculate the horizontal velocity
The horizontal velocity (v_x) remains constant because there is no horizontal acceleration (neglecting air resistance). Thus:
vx=15 m/s
Step 3: Calculate the vertical velocity just before hitting the ground
Using the vertical motion equation, we can find the final vertical velocity (v_y) just before hitting the ground:
vy=uy+gt
Substituting the values:
vy=0+9.8⋅10=98 m/s
Step 4: Calculate the resultant velocity when the stone hits the ground
The resultant velocity (v) can be found using the Pythagorean theorem, since the horizontal and vertical components are perpendicular to each other:
v=√v2x+v2y
Substituting the values:
v=√(15)2+(98)2=√225+9604=√9829
Calculating the square root:
v≈99.14 m/s
Final Answer
Thus, the speed with which the stone hits the ground is approximately 99.14 m/s.
---
We know the height of the cliff (h) is 490 m, and the initial vertical velocity (u_y) is 0 m/s (since the stone is thrown horizontally). We can use the following kinematic equation for vertical motion:
The horizontal velocity (v_x) remains constant because there is no horizontal acceleration (neglecting air resistance). Thus:
Using the vertical motion equation, we can find the final vertical velocity (v_y) just before hitting the ground:
The resultant velocity (v) can be found using the Pythagorean theorem, since the horizontal and vertical components are perpendicular to each other:
Thus, the speed with which the stone hits the ground is approximately 99.14 m/s.
Topper's Solved these Questions
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:NCERT BASED QUES. SINGLE ANS.
Explore 8 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:NCERT BASED QUES. MORE THAN ONE OPTION
Explore 6 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(C.W)
Explore 45 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
Similar Questions
A hiker stands on the edge of a cliff 490m above the ground and throwns a stone horiozontally with an initial speed of 15ms−1 neglecting air resistance.The time taken by the stone to reach the ground in seconds is (g=9.8ms2)
View SolutionA hiker stands on the edge of horizontally with an initial speed if 15ms−1 . Negkectubg aur resustabce, find the time taken by the stone to reach the ground, and the speed with which it hits the ground. Take g=9.8m/s2.
View Solution
Knowledge Check
A hiker stands on the edge of a cliff 490m above the ground and throwns a stone horiozontally with an initial speed of 15ms−1 neglecting air resistance.The time taken by the stone to reach the ground in seconds is (g=9.8ms2)
A5B10C1D5In the above problem, the initial speed with which water strikes the ground in ms−1 is
A10B5C5√2D10√2A stone is thrown horizontally with velocity gms−1 from the top of a tower of height g metre. The velocity with which it hits the ground is (inms−1)
AgB2gC√3gD4g
From the top of a 490 m high cliff, a boy throws a stone horizontally with a initial speed of 15ms−1. What is the time taken by the stone to reach the ground.
View SolutionA stone is thrown vertically upwards with a velocity of 4.9ms−1. Calculate : the velocity with which it returns to the ground.
View SolutionA ball is projected form ground with a speed of 20 ms^(-1)
View SolutionA woman stands on the edge of a cliff and throws a stone vertically downward with an initial speed of 10 m/s. The instant before the stone hits the ground below, it has 450 J of kinetic energy. If she were to throw the stone horizontally outward from the cliff with the same initial speed of 10 m/s, how much kinetic energy would it have just before it hits the ground ?
View SolutionA motor cyclist is trying to jump across a path as shown by driving horizontally off a cliff A at a speed of 5ms−1. Ignore air resistance and take g=10ms−2. The speed with which he touches the peak B is:
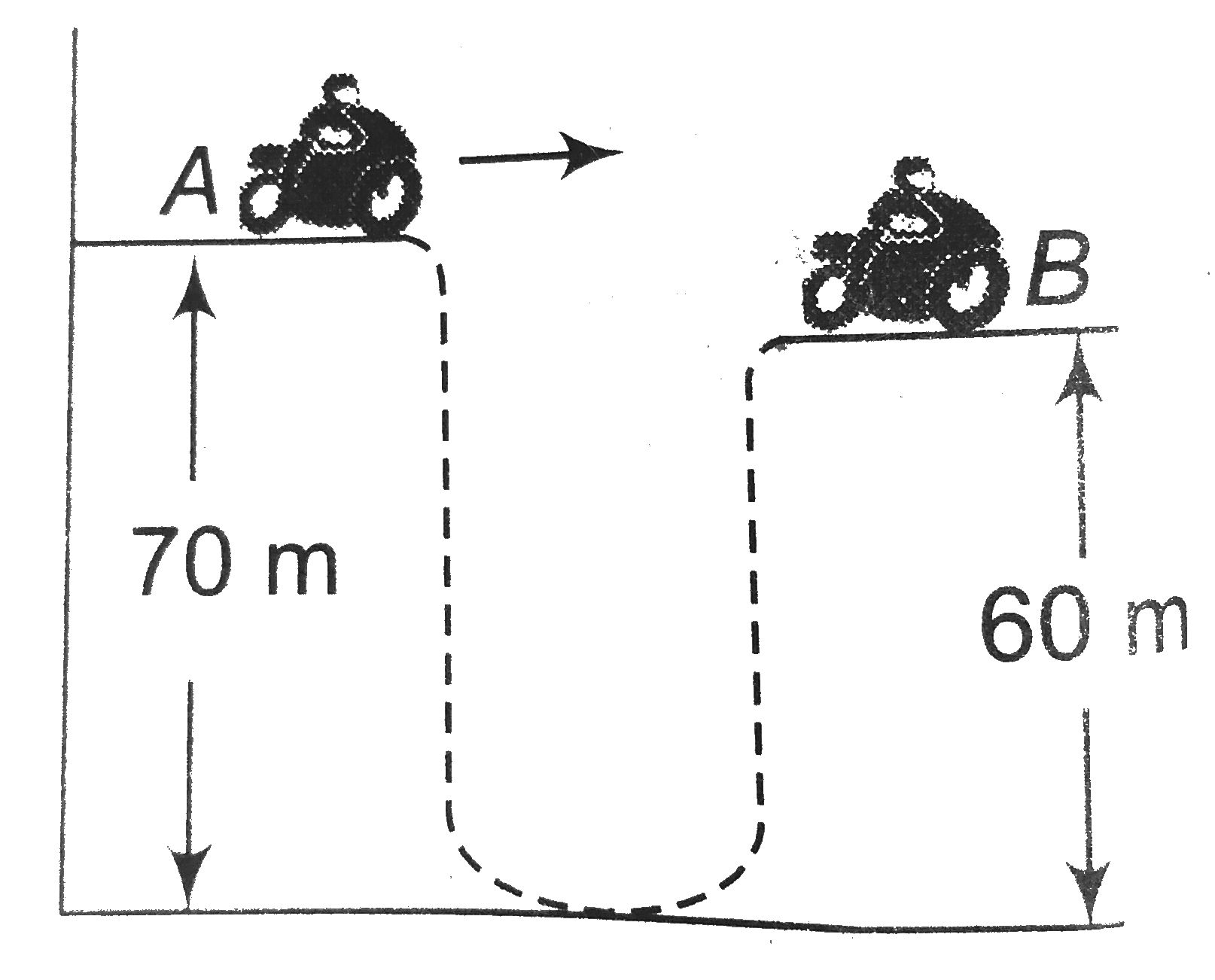
View Solution

