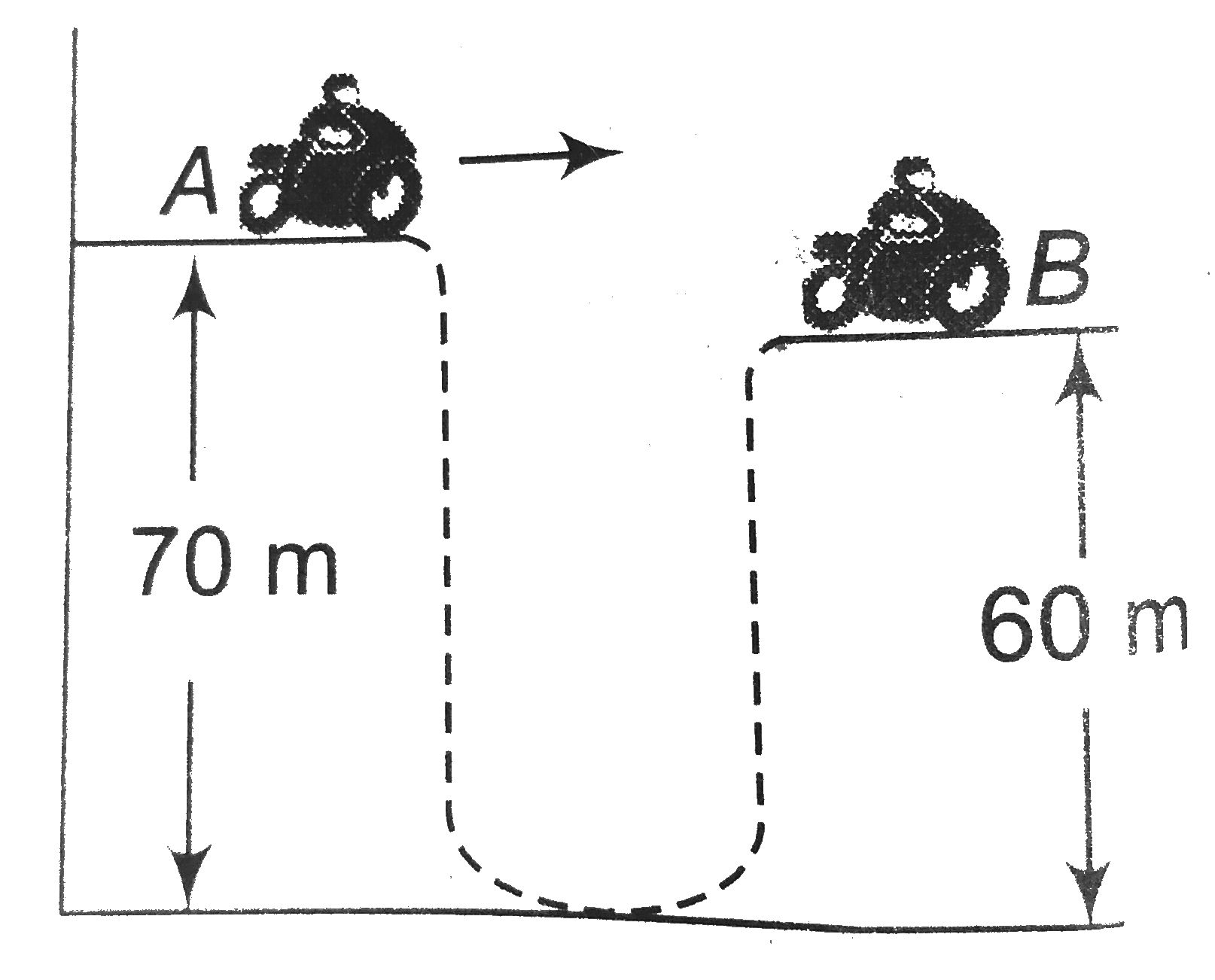
A motor cyclist is trying to jump across a path as shown by driving horizontally off a cliff A at a speed of 5ms−1. Ignore air resistance and take g=10ms−2. The speed with which he touches the peak B is:
2.0ms−1
15ms−1
25ms−1
20ms−1
The correct Answer is:B
Speed in horizontal direction remains constant during whole journey because there is no acceleration in this direction.
So, vh=6ms−1
In vertical direction:
Loss of gravitational potential energy =gain in KE
i.e., mgh=12mv2V
V2V=2gh=2×10×(70−60)=200
Hence, the speed with which he touches the cliff B is :
v=√v2h+v2V=√25+200=√225=15ms−1
Topper's Solved these Questions
Similar Questions
A hiker stands on the edge of a cliff 490m above the ground and throwns a stone horiozontally with an initial speed of 15ms−1 neglecting air resistance.The time taken by the stone to reach the ground in seconds is (g=9.8ms2)
View SolutionA projectile is thrown horizontally with a speed of 20ms−1 .If g is (10ms−2) ,then the speed of the projectile after 5 second will be nearly
View Solution
Knowledge Check
A motor cyclist is trying to jump across a path as shown by driving horizontally off a cliff A at a speed of 5ms−1. Ignore air resistance and take g=10ms−2. The speed with which he touches the cliff B is
 A2.0ms−1B12ms−1C25ms−1D15ms−1
A2.0ms−1B12ms−1C25ms−1D15ms−1A hiker stands on the edge of a cliff 490m above the ground and throwns a stone horiozontally with an initial speed of 15ms−1 neglecting air resistance.The speed with which it hits the ground in ms−1 is (g=9.8ms2)
A9.8B99C4.9D49A hiker stands on the edge of a cliff 490m above the ground and throwns a stone horiozontally with an initial speed of 15ms−1 neglecting air resistance.The time taken by the stone to reach the ground in seconds is (g=9.8ms2)
A5B10C1D5
How much work should be done on a bicycle of mass 20 kg to increase its speed from 2ms−1 to 5ms−1 ? (Ignore air resistance and friction).
View SolutionA body is projected vertically up with a speed of 20ms−1 .The distance travelled by it in "3" seconds it (g=10ms−2)
View SolutionA cyclist is moving on a smooth horizontal curved path of radius of curvature 10m .With a speed 10ms^(-1).Then his angle of leaning is (g=10ms^(-1))
View SolutionA body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5 second? (g=10ms−2)
View SolutionA body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5s ? (g=10ms−2).
View Solution

