A plane surface is inclined making an angle above the horizon. A bullet is fired with the point of projection at the bottom of the inclined plane with velocity u, then the maximum range is given by:
The correct Answer is:b
To solve the problem of finding the maximum range of a bullet fired from the bottom of an inclined plane, we can follow these steps:
Step 1: Understand the Setup
We have a plane inclined at an angle β to the horizontal. A bullet is fired from the bottom of this inclined plane with an initial velocity u. We need to determine the angle of projection α that maximizes the range of the bullet along the inclined plane.
Step 2: Resolve the Initial Velocity
The initial velocity u can be resolved into two components:
- The component along the incline (x-direction): ux=ucosα
- The component perpendicular to the incline (y-direction): uy=usinα
Step 3: Analyze the Motion
The bullet experiences two types of motion:
1. Horizontal motion along the incline (x-direction).
2. Vertical motion perpendicular to the incline (y-direction).
Step 4: Write the Equations of Motion
Using the equations of motion, we can express the position in the x and y directions as functions of time t:
- For x-direction (along the incline):
x=ux⋅t=ucosα⋅t
- For y-direction (perpendicular to the incline):
y=uy⋅t−12gcosβ⋅t2=usinα⋅t−12gcosβ⋅t2
Step 5: Determine the Time of Flight
At the point where the bullet returns to the incline (y = 0), we can set up the equation:
0=usinα⋅t−12gcosβ⋅t2
Factoring out t (noting t≠0):
t(usinα−12gcosβ⋅t)=0
Thus, solving for t:
t=2usinαgcosβ
Step 6: Calculate the Range
Substituting the time of flight back into the equation for x:
R=ucosα⋅t=ucosα⋅2usinαgcosβ
This simplifies to:
R=2u2sinαcosαgcosβ
Step 7: Use Trigonometric Identity
Using the identity 2sinαcosα=sin(2α), we can rewrite the range as:
R=u2sin(2α)gcosβ
Step 8: Maximize the Range
To maximize R, we need to maximize sin(2α). The maximum value of sin(2α) is 1, which occurs when:
2α=π2⟹α=π4
Step 9: Substitute Back to Find Maximum Range
Substituting α=π4 into the range equation:
Rmax=u2gcosβ
Step 10: Final Expression
Considering the effect of the angle β, the maximum range along the inclined plane can be expressed as:
Rmax=u2(1+sinβ)gcosβ
Conclusion
Thus, the maximum range of the bullet fired from the inclined plane is given by:
Rmax=u2g(1+sinβ)
We have a plane inclined at an angle β to the horizontal. A bullet is fired from the bottom of this inclined plane with an initial velocity u. We need to determine the angle of projection α that maximizes the range of the bullet along the inclined plane.
The initial velocity u can be resolved into two components:
- The component along the incline (x-direction): ux=ucosα
- The component perpendicular to the incline (y-direction): uy=usinα
The bullet experiences two types of motion:
1. Horizontal motion along the incline (x-direction).
2. Vertical motion perpendicular to the incline (y-direction).
Using the equations of motion, we can express the position in the x and y directions as functions of time t:
- For x-direction (along the incline):
x=ux⋅t=ucosα⋅t
- For y-direction (perpendicular to the incline):
y=uy⋅t−12gcosβ⋅t2=usinα⋅t−12gcosβ⋅t2
At the point where the bullet returns to the incline (y = 0), we can set up the equation:
0=usinα⋅t−12gcosβ⋅t2
Factoring out t (noting t≠0):
t(usinα−12gcosβ⋅t)=0
Thus, solving for t:
t=2usinαgcosβ
Substituting the time of flight back into the equation for x:
R=ucosα⋅t=ucosα⋅2usinαgcosβ
This simplifies to:
R=2u2sinαcosαgcosβ
Using the identity 2sinαcosα=sin(2α), we can rewrite the range as:
R=u2sin(2α)gcosβ
To maximize R, we need to maximize sin(2α). The maximum value of sin(2α) is 1, which occurs when:
2α=π2⟹α=π4
Substituting α=π4 into the range equation:
Rmax=u2gcosβ
Considering the effect of the angle β, the maximum range along the inclined plane can be expressed as:
Rmax=u2(1+sinβ)gcosβ
Thus, the maximum range of the bullet fired from the inclined plane is given by:
Rmax=u2g(1+sinβ)
Topper's Solved these Questions
Similar Questions
A mass m slides down a fixed plane inclined at an angle a to the horizontal plane after covering the entire length of the inclined plane. The height of the inclined plane is h and the coefficient of friction over both surfaces is μ.
View SolutionThe normal component of the velocity of projectile projected from the bottom of an inclined plane remains unchanged in magnitude when it lands on the plane.
View Solution
Knowledge Check
An inclined plane making an angle β with horizontal. A projectile projected from the bottom of the plane with a speed u at angle α with horizontal, then its maximum range Rmax is
ARmax=u2g(1−sinβ)BRmax=u2g(1+sinβ)CRmax=u2g(1−sinβ)DRmax=u2g(1+sinβ)An inclined plane is inclined at an angle θ with the horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
AmgsinθBμmgcosθCμmgcosθ−mgsinθDμmgcosθ+mgsinθThe ratio of the range of the particle and its maximum range in the inclined plane is:
A1:2B1:√2C1:√3D1:1
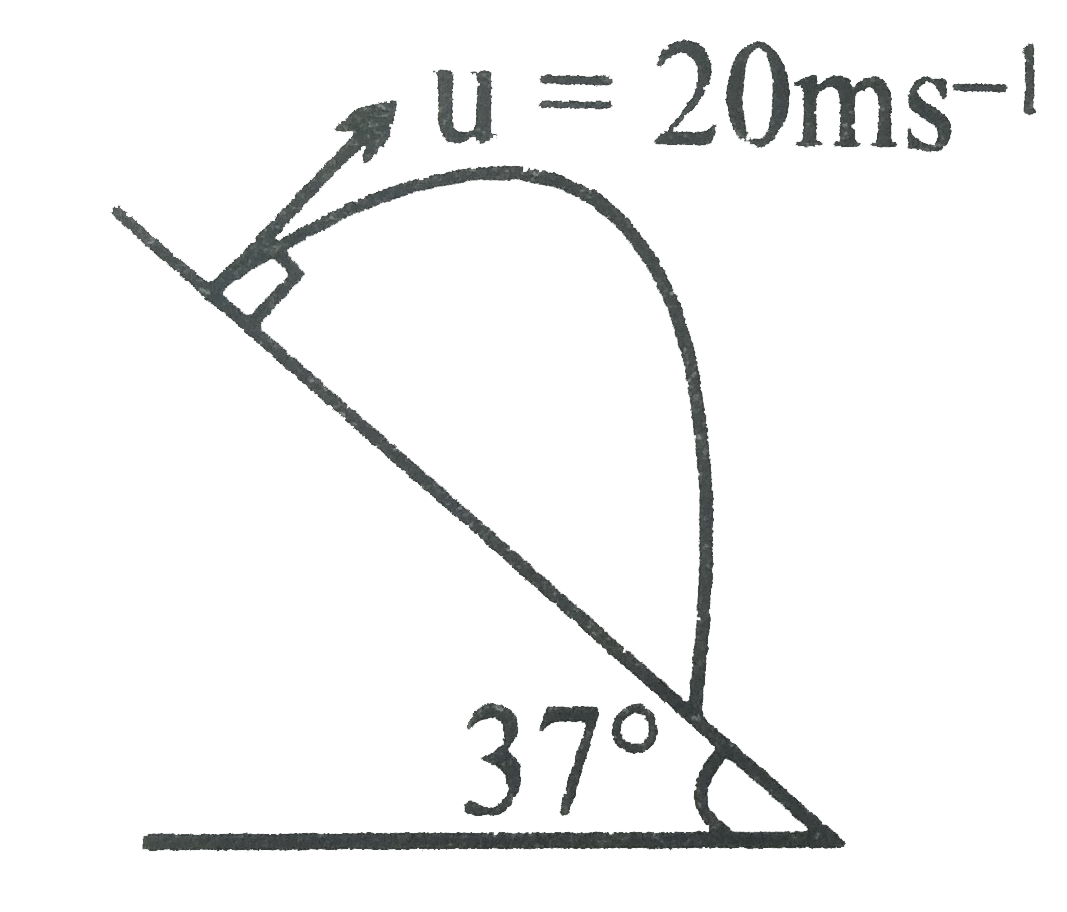
Find range of projectile on the inclined plane which is projected perpendicular to the incline plane with velcoity 20m/s as shwon in figure.
View SolutionAn inclined plane of height h and length l have the angle of inclination θ. The time taken by a body to come from the top of the bottom of this inclined plane will be
View Solution
A particle is projected from surface of the inclined plane with speed u and at an angle θ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is

View SolutionA particle is projected from the inclined plane at angle 37∘ with the inclined plane in upward direction with speed 10m/s. The angle of inclined plane with horizontal is 53∘. Then the maximum height attained by the particle from the inclined plane will be-
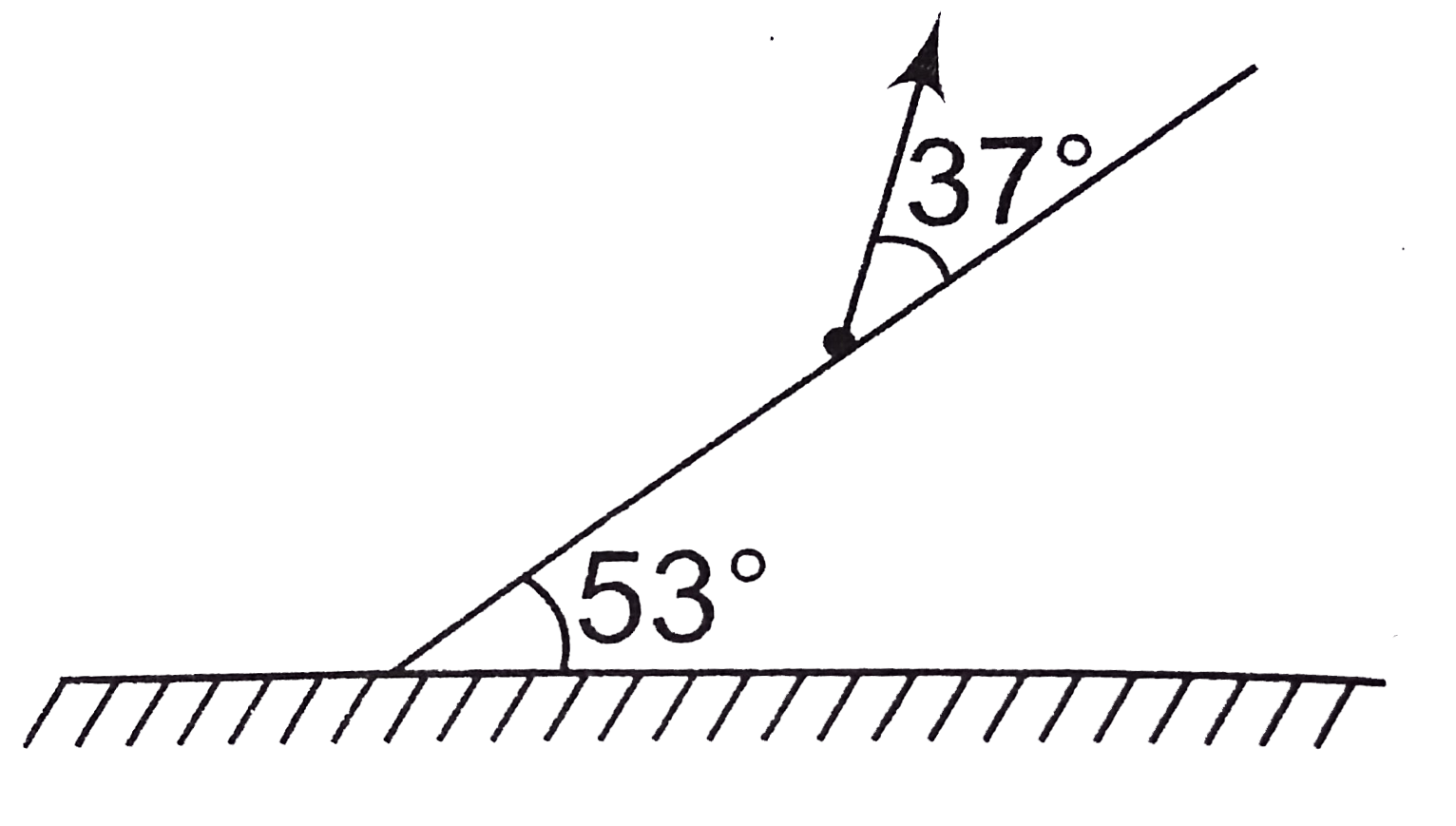
View Solution

