For body moving with uniform acceleration , initial and final velocities in a time interval are and respectively. Then its average velocity in the time interval is
The correct Answer is:B
To find the average velocity of a body moving with uniform acceleration, we can follow these steps:
1. Understand the Given Information:
- The body has an initial velocity u and a final velocity v.
- The acceleration is uniform, denoted as a.
- The time interval during which this motion occurs is t.
2. Formula for Average Velocity:
- The average velocity vavg can be defined as the total distance traveled divided by the total time taken:
vavg=st
where s is the distance traveled during the time interval t.
3. Distance Traveled with Uniform Acceleration:
- The formula for distance s when an object is moving with uniform acceleration is given by:
s=ut+12at2
4. Substituting for Average Velocity:
- Substitute the expression for s into the average velocity formula:
vavg=ut+12at2t
- Simplifying this gives:
vavg=u+12at
5. Relate Final Velocity to Initial Velocity:
- From the equation of motion, we know:
v=u+at
- Rearranging this gives:
u=v−at
6. Substituting u in Average Velocity Formula:
- Now substitute u in the average velocity formula:
vavg=(v−at)+12at
- Simplifying this gives:
vavg=v−at+12at=v−12at
7. Final Expression for Average Velocity:
- Thus, the average velocity can be expressed as:
vavg=v−12at
Conclusion:
The average velocity vavg of the body moving with uniform acceleration over the time interval t is given by:
vavg=u+12at
or equivalently,
vavg=v−12at
- The body has an initial velocity u and a final velocity v.
- The acceleration is uniform, denoted as a.
- The time interval during which this motion occurs is t.
- The average velocity vavg can be defined as the total distance traveled divided by the total time taken:
vavg=st
where s is the distance traveled during the time interval t.
- The formula for distance s when an object is moving with uniform acceleration is given by:
s=ut+12at2
- Substitute the expression for s into the average velocity formula:
vavg=ut+12at2t
- Simplifying this gives:
vavg=u+12at
- From the equation of motion, we know:
v=u+at
- Rearranging this gives:
u=v−at
- Now substitute u in the average velocity formula:
vavg=(v−at)+12at
- Simplifying this gives:
vavg=v−at+12at=v−12at
- Thus, the average velocity can be expressed as:
vavg=v−12at
The average velocity vavg of the body moving with uniform acceleration over the time interval t is given by:
vavg=u+12at
or equivalently,
vavg=v−12at
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 C.W
Explore 25 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 3 C.W
Explore 25 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:C.U.Q
Explore 42 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
Similar Questions
For a body moving withuniform acceleration 'a', initial and final velocities in a time interval are 'u' and respectively.Then,its average velocity in the time interval T is
View SolutionA particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
View Solution
Knowledge Check
Statement-I : A particle moves in a straight line with constant acceleration. The average velocity of this particle cannot be zero in any time interval.
Statement-II : For a particle moving in straight line with constant acceleration, the average velocity in a time interval is u+v2, where u and v are initial and final velocity of the particle of the given time interval.AStatement-I is true, Statement-II is true, Statement-II is correct explanation for Statement-IBStatement-I is true, Statement-II is true, Statement-II is NOT a correct explanation for Statement-ICStatement-I is true, Statement-II is falseDStatement-I is false, Statement-II is true.An object is moving with uniform acceleration a. Its initial velocity is u and after time t its velocity is v. The equation of its motion is v = u + at. The velocity (along y-axis) time (along x-axis) graph shall be a straight line
Apassing through originBwith x-intercept uCwith y-intercept uDwith slope uWhen electric field is applied inside a conductor then free electron are accelerated. Their average velocity in time interval t is proportional to
At1Bt2C√tDt0
A particle move with a velocity v=αt3 along a straight line.The average velocity in time interval t=0 to t=T is
View SolutionProve that average velocity of an object can never be greater than the average speed of an object over a given interval of time.
View SolutionA body A moves with a uniform acceleration a and zero initial velocity. Another body B, starts from the same point moves in the same direction with a constant velocity v. The two bodies meet after a time t. The value of t is
View SolutionAssertion : In the υ−t diagram as shown in figure, average velocity between the interval t = 0 and t=t0 is independent of t0
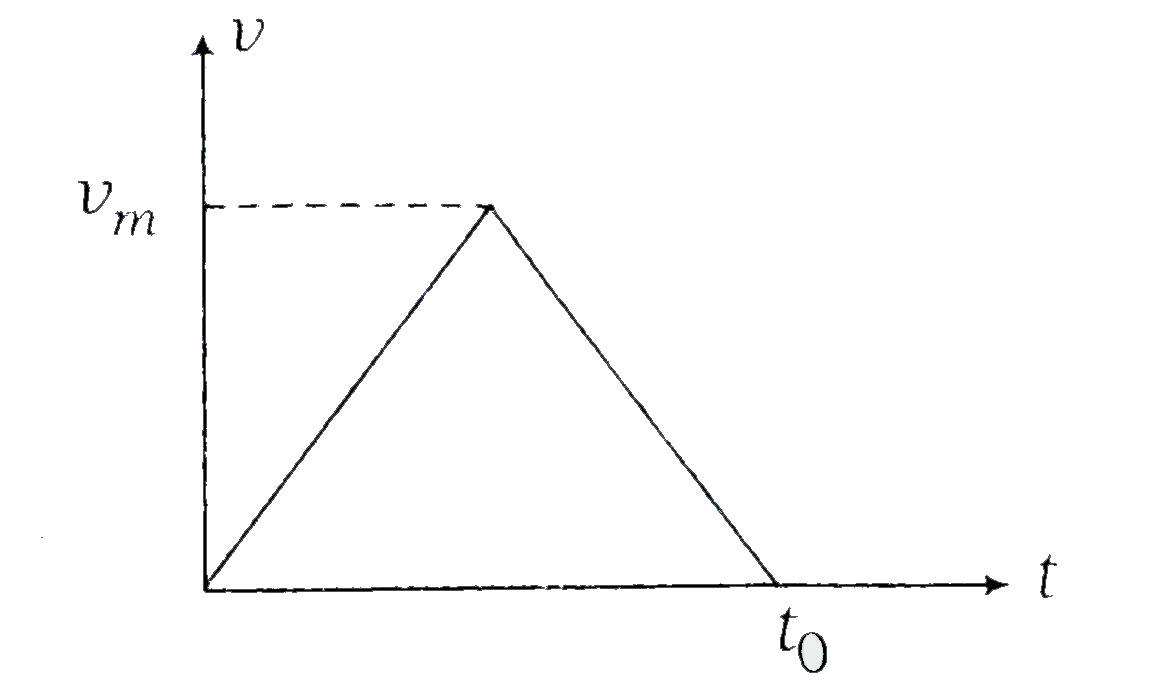
Reason : Average velocity in the given interval is 12υm.
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View Solution