A body A moves with a uniform acceleration a and zero initial velocity. Another body B, starts from the same point moves in the same direction with a constant velocity v. The two bodies meet after a time t. The value of t is
To solve the problem, we need to analyze the motion of both bodies A and B and set up equations for their positions at time t.
Step 1: Write the equation of motion for body A
Body A starts from rest (initial velocity uA=0) and moves with uniform acceleration a. The equation of motion for body A can be given by:
xA=uAt+12at2
Since uA=0, the equation simplifies to:
xA=12at2
Step 2: Write the equation of motion for body B
Body B starts from the same point and moves with a constant velocity v. The equation of motion for body B is:
xB=vt
Step 3: Set the positions equal to each other
Since both bodies meet after time t, their positions will be equal:
xA=xB
Substituting the equations we derived:
12at2=vt
Step 4: Rearrange the equation
To solve for t, we can rearrange the equation:
12at2−vt=0
Factoring out t:
t(12at−v)=0
Step 5: Solve for t
This gives us two solutions:
1. t=0 (the initial time when both bodies start)
2. 12at−v=0
From the second equation, we can solve for t:
12at=v⟹t=2va
Final Answer
Thus, the time t at which both bodies meet is:
t=2va
---
Body A starts from rest (initial velocity uA=0) and moves with uniform acceleration a. The equation of motion for body A can be given by:
xA=uAt+12at2
Since uA=0, the equation simplifies to:
xA=12at2
Body B starts from the same point and moves with a constant velocity v. The equation of motion for body B is:
xB=vt
Since both bodies meet after time t, their positions will be equal:
xA=xB
Substituting the equations we derived:
12at2=vt
To solve for t, we can rearrange the equation:
12at2−vt=0
Factoring out t:
t(12at−v)=0
This gives us two solutions:
1. t=0 (the initial time when both bodies start)
2. 12at−v=0
12at=v⟹t=2va
Thus, the time t at which both bodies meet is:
t=2va
Topper's Solved these Questions
Similar Questions
Knowledge Check
A body is moving with uniform acceleration. Its 'velocity
Awill be increasing,Bwill be decreasing,Cwill be uniform,Dwill increase first and decrease afterward.A body A starts from rest and moves with a uniform acceleration along a straight line. Another body B has some initial velocity and moves with larger acceleration than that of A. The correct velocity time graphs
A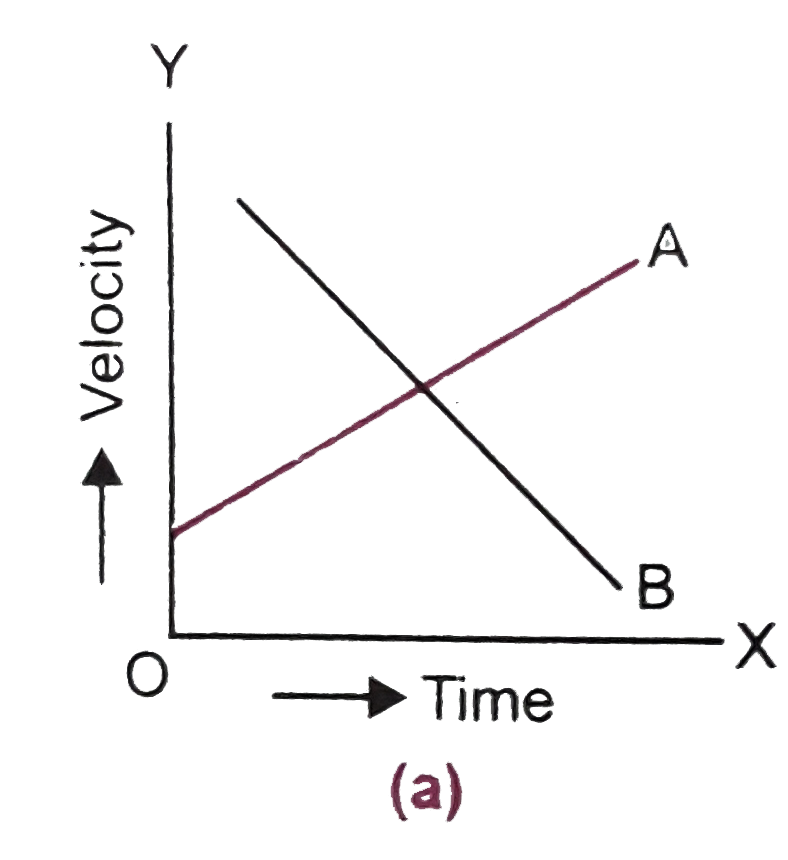 B
B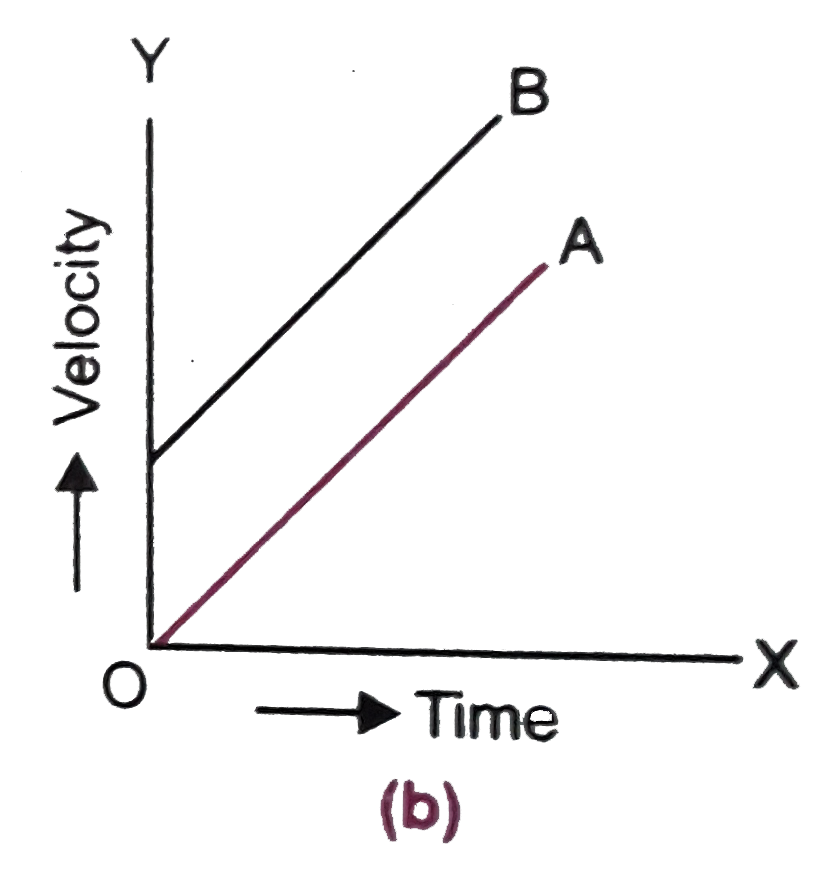 C
C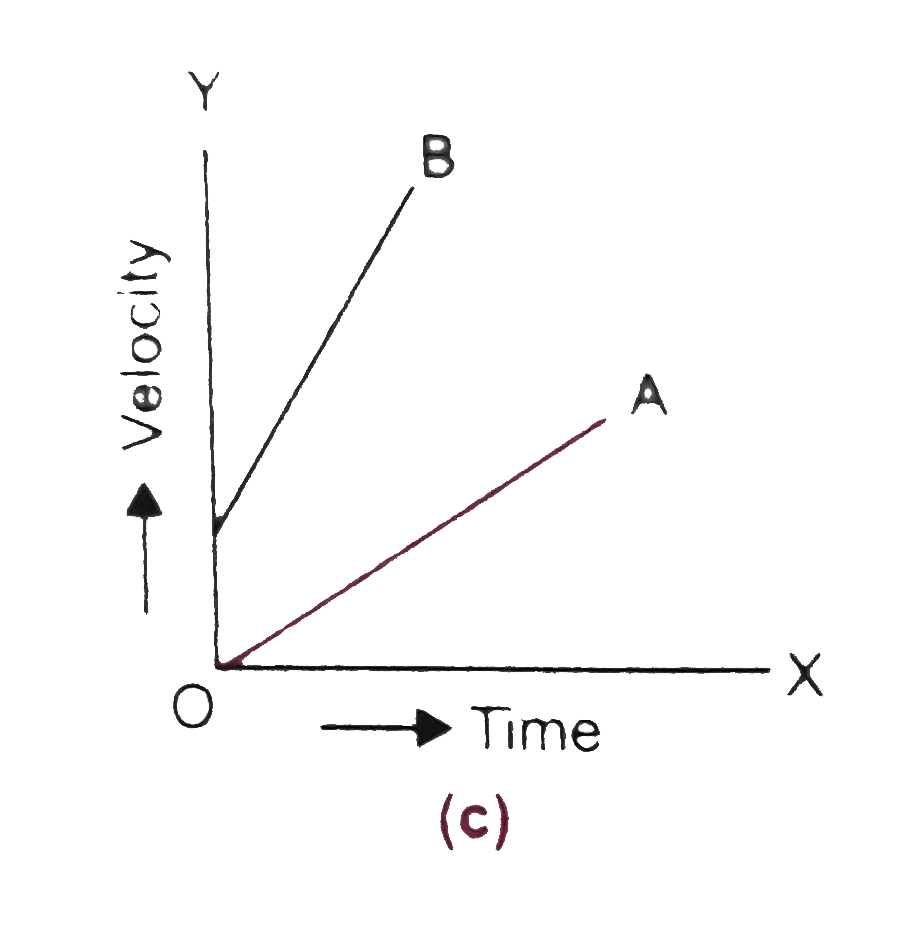 D
D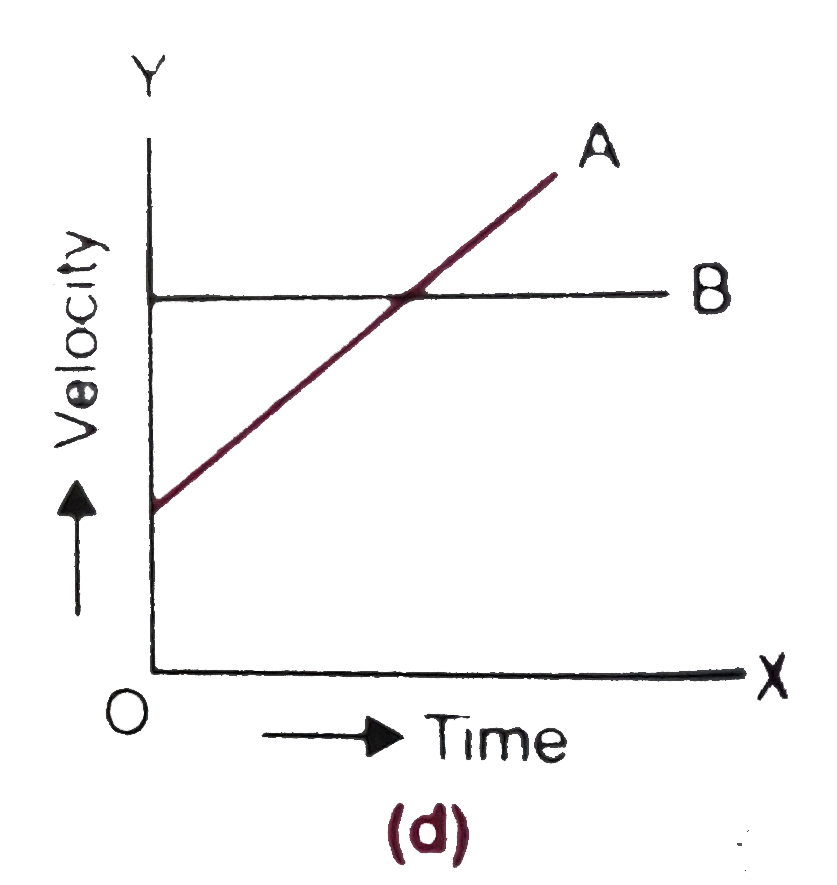
A body starts from rest with uniform acceleration. The velocity of the body after t seconds is v. The displacement of the body in last three seconds is
A3v2(t−3)B3v2(t+3)C3v[1−32t]D3v[1+32t]
A car starts from rest and moves with uniform acceleration a, At the same instant from the same point a bike crosses with a uniform velocity u. When and there will they meet ? What is the velocity of car with respect to the bike at the time of meeting?
View SolutionA body starts from rest and then moves with uniform acceleration. Then.
View SolutionA body of mass 1.0 kg strikes elastically with another body at rest and continues to move in the same direction with one-fourth of its initial velocity. The mass of the other body is
View SolutionA body is at rest at x=0 . At t=0, it starts moving in the positive x−direction with a constant acceleration . At the same instant another body passes through x=0 moving in the positive x−direction with a constant speed . The position of the first body is given by x1(t) after time 't', and that of the second body by x2(t) after the same time interval . which of the following graphs correctly describes (x1−x2) as a function of time 't' ?
View SolutionA body falls freely from a height of 50 m. Simultaneously, another body is thrown from the surface of earth with a certain initial velocity. The two bodies meet at a height of 10 m. What is the initial velocity of the second body ?
View Solution

