A "bar" magnet of magnetic moment M is bent in '∪' shape such that all the parts are of equal lengths. Then new magnetic moment is
M/3
2M
√3M
3√3M
The correct Answer is:A
To solve the problem of finding the new magnetic moment of a bar magnet bent into a 'U' shape, we can follow these steps:
Step 1: Understand the Initial Magnetic Moment
The magnetic moment M of a bar magnet is given by the formula:
M=m⋅L
where m is the pole strength and L is the length of the magnet.
Step 2: Analyze the U-shaped Configuration
When the bar magnet is bent into a 'U' shape, the total length remains the same, but the configuration changes. If the original length of the magnet is L, when bent into a 'U' shape, each arm of the 'U' will have a length of L3.
Step 3: Determine the New Distance Between the Poles
In the 'U' shape, the distance D between the north pole and the south pole becomes the length of one arm of the 'U', which is:
D=L3
Step 4: Calculate the New Magnetic Moment
The new magnetic moment M′ for the bent magnet can be calculated using the same formula for magnetic moment:
M′=m⋅D
Substituting D with L3:
M′=m⋅L3
Step 5: Relate the New Magnetic Moment to the Original
Since the original magnetic moment M is m⋅L, we can express m as:
m=ML
Now substituting this into the equation for M′:
M′=(ML)⋅L3
This simplifies to:
M′=M3
Final Answer
Thus, the new magnetic moment M′ after bending the bar magnet into a 'U' shape is:
M′=M3
The magnetic moment M of a bar magnet is given by the formula:
M=m⋅L
where m is the pole strength and L is the length of the magnet.
When the bar magnet is bent into a 'U' shape, the total length remains the same, but the configuration changes. If the original length of the magnet is L, when bent into a 'U' shape, each arm of the 'U' will have a length of L3.
In the 'U' shape, the distance D between the north pole and the south pole becomes the length of one arm of the 'U', which is:
D=L3
The new magnetic moment M′ for the bent magnet can be calculated using the same formula for magnetic moment:
M′=m⋅D
Substituting D with L3:
M′=m⋅L3
Since the original magnetic moment M is m⋅L, we can express m as:
m=ML
Now substituting this into the equation for M′:
M′=(ML)⋅L3
This simplifies to:
M′=M3
Thus, the new magnetic moment M′ after bending the bar magnet into a 'U' shape is:
M′=M3
Topper's Solved these Questions
- MAGNETISMBook:NARAYNAChapter:MAGNETISMExercise:LEVEL-II(C.W)
Explore 42 Videos
- MAGNETISMBook:NARAYNAChapter:MAGNETISMExercise:LEVEL-III(C.W)
Explore 30 Videos
- MAGNETISMBook:NARAYNAChapter:MAGNETISMExercise:C.U.Q (ASSERTION & REASON)
Explore 13 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
Similar Questions
Knowledge Check
A bar magnet of magnetic moment M is bent in
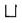 shape such that all the parts are of equal lengths. Then new magnetic moment is AM/3B2MC√3MD3√3M
shape such that all the parts are of equal lengths. Then new magnetic moment is AM/3B2MC√3MD3√3MA bar magnet of magnetic moment M is bent in
 shape with equal arm lengths.The new magnet moment isAMBM/2CM/3DM
shape with equal arm lengths.The new magnet moment isAMBM/2CM/3DMA magnet of magnetic moment M and length 2l is bent at its mid-point such that the angle of bending is 600. The new magnetic moment is.
AMBM2C2MDM√2
A magnetic wire magnetic moment M is bent into a shape
 with all segments of equal length the new magnetic moment is
with all segments of equal length the new magnetic moment is
View SolutionA bar magnet of moment M is bent into arc, its moment
View SolutionA bar magnet of moment 'M' is bent into a shape
 . If the length of the each part is same, its new magnetic moment will be
. If the length of the each part is same, its new magnetic moment will be
View SolutionA thin "bar" magnet of length 'l' and magnetic moment 'M' is bent at the mid point so that the two parts are at right angles. The new magnetic length and magnetic moment are respectively
View SolutionA bar magnet of moment 'M' is bent into a shape '5'. If the length of the each part is same, its new magnetic moment will be
View Solution
