Shown a conductor of length l having a circular cross section. The radius of cross section varies linearly form a→b. The resistivity of the material is(ρ).Assuming that b−a<<l,find the resistance of the conductor.

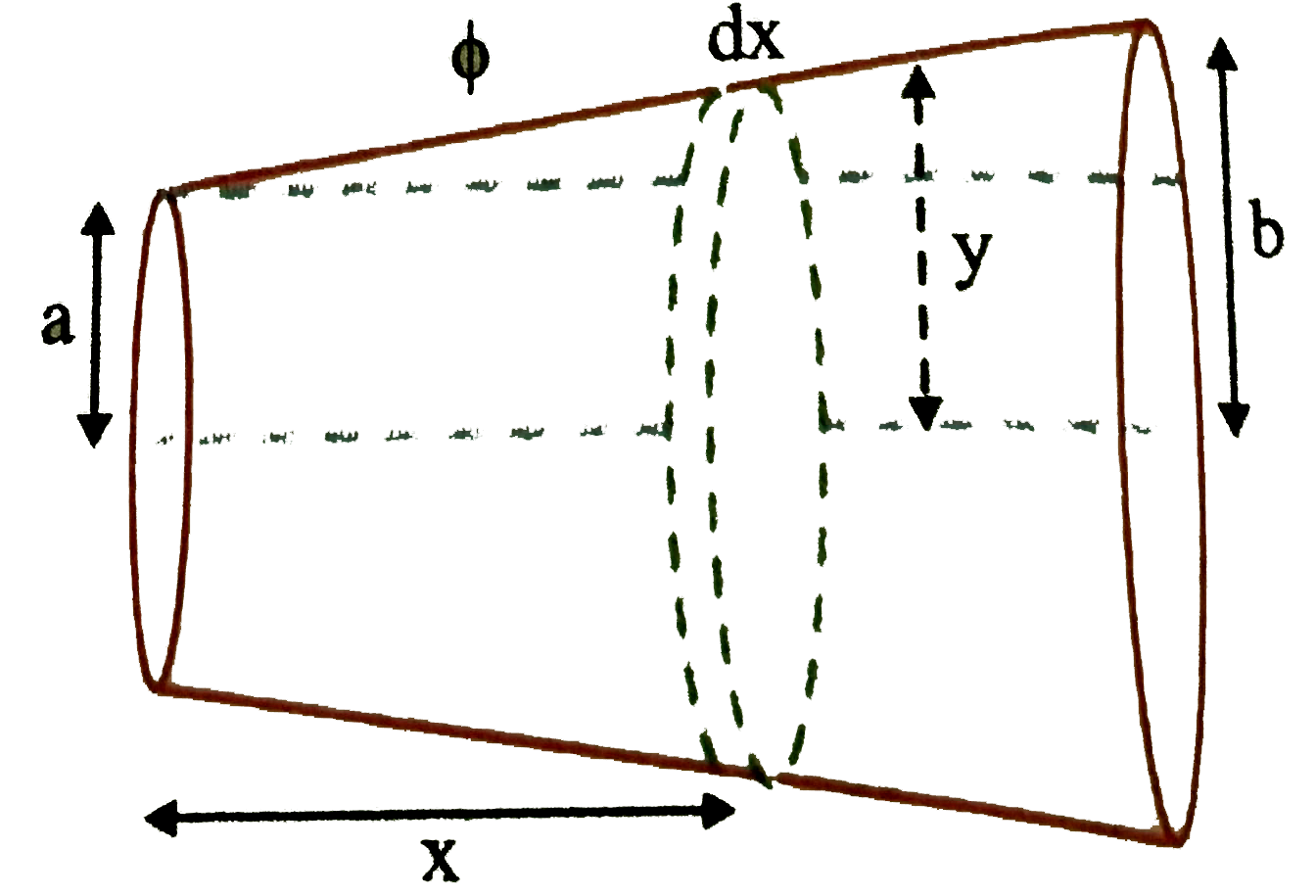
tanϕ=b−al=y−ax
yl−al=bx−ax
l(dydx)=(b−a)⇒dx=(lb−a)dy→(1)
Resistance across the elemetal disc under consideration dR=ρdxA→(2)
From (1) and (2) dR=ρ(lb−a)dyπy2
⇒ Resistance across the given conductor,
R=∫by=adR⇒R=ρlπ(b−a)∫y=by=adyy2,∵R=ρlπab
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - C.U.Q
105 Videos
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 C.W
64 Videos
- COMMUNICATION SYSTEMBOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)
25 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NARAYNACHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ASSERTION AND REASON
15 Videos
Similar Questions
Figure shows a conductor of length l having a circular cross-section. The radius of cross-section varies linearly from a to b. Find the resistance of the conductor. ltbtgt

View SolutionA conductor of length l has a non-uniform cross-section. The radius of cross-section varies linearly from a to b. The resistivity of the material is ρ. Find the resistance of the conductc across its ends.

View Solution
Knowledge Check
A conductor of length l and area of cross-section A has a resistance R then its specific resistance is
Aρ=RAlBρ=RAlCρ=lRADρ=R2AlResistivity of a conductor of length l and cross - section A is ρ . If its length is doubled and area of cross-section is halved, then its new resistivity will be .
Aρ2B4ρCρ4DρTwo copper wires A and B of length l and 2l respectively, have the same area of cross-section. The ratio of the resistivity of wire A to the resistivity of wire B is
A4B2C1D1/2
A wire of length 10 cm and area of cross section 1mm2 has a resistance of 5Ω. Find the resistivity of the material of the wire.
View SolutionA conductor in the shape of a cylinder of length l and cross sectional radius r is connected to a cell of emf V. The resistivity of the material of the conductor is ρ and does not change much with temperature. The emissivity of the curved surface of the conductor is e. [Take emissivity of the flat circular surfaces to be zero]. In steady state the temperature of the conductor is T when the environmental temperature is T0. The difference between TandT0 is much smaller than the environmental temperature. Stefan’s Constant is σ.
Find the steady state temperature T for the conductor.
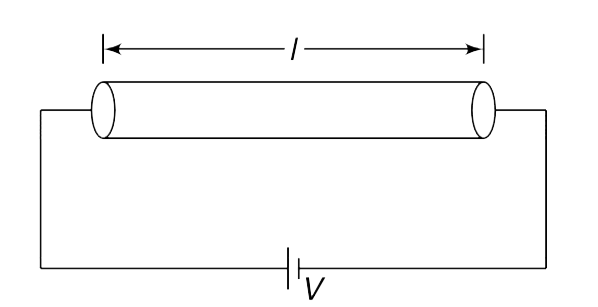
View SolutionThermal resistance R of a conductor of length l cross section A and conuctivity K is
View Solution" A wire of length L and resistance "R" is stretched to get the radius of cross-section halved.What is the new resistance "
View SolutionThe resistance of the material of unit length and unit area of cross section is
View Solution