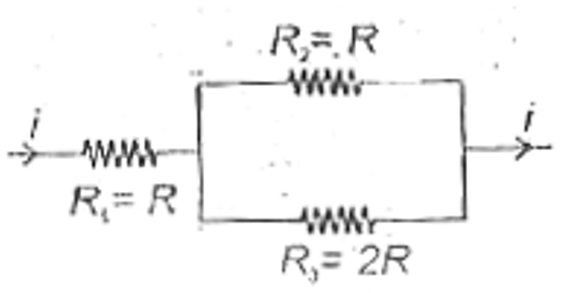
In the given network, the powers generated in the resistor R1 and R2 are P1 and P2 and the power generated in R is P. For this network.
if P1=P2 it necessarily follows that R1=R2
if R=R1+R2, then P>P1+P2
if P=P1+P2 then R≤R1+R24
if R1=R2 then it necessarily follows that P=P1+P2
The correct Answer is:A, B, C
(A). If P1=P2,V2R1=V2R2 Where V is the difference of potential from P to Q. Hence R1=R2
(B). P=i2R=i2(R1+R2)=i2R1+i2R2>i21R1+i22R2
since i>i1 and i>i2 Hence P>P1+P2
(C). let P=P1+P2 then i2R=i21R1+i22R2
but i=i1+i2⇒(i1+i2)2R=i21R1+i22R2
now (i1+i2)2=(i1−i2)2+4i1i2
Since i1 and i2 are both positive, maximum value of (i1+i2) is when i1=i2=i2
Then from (1), 4R=R1+R2
Hence maximum value R can have consistent with
P=P1+P2 is R1+R24 Hence R≤R1+R24
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NARAYNAChapter:CURRENT ELECTRICITYExercise:Level 5
Explore 42 Videos
- COMMUNICATION SYSTEMBook:NARAYNAChapter:COMMUNICATION SYSTEMExercise:Level-II(H.W)
Explore 25 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:NARAYNAChapter:DUAL NATURE OF RADIATION AND MATTERExercise:ASSERTION AND REASON
Explore 15 Videos
Similar Questions
Knowledge Check
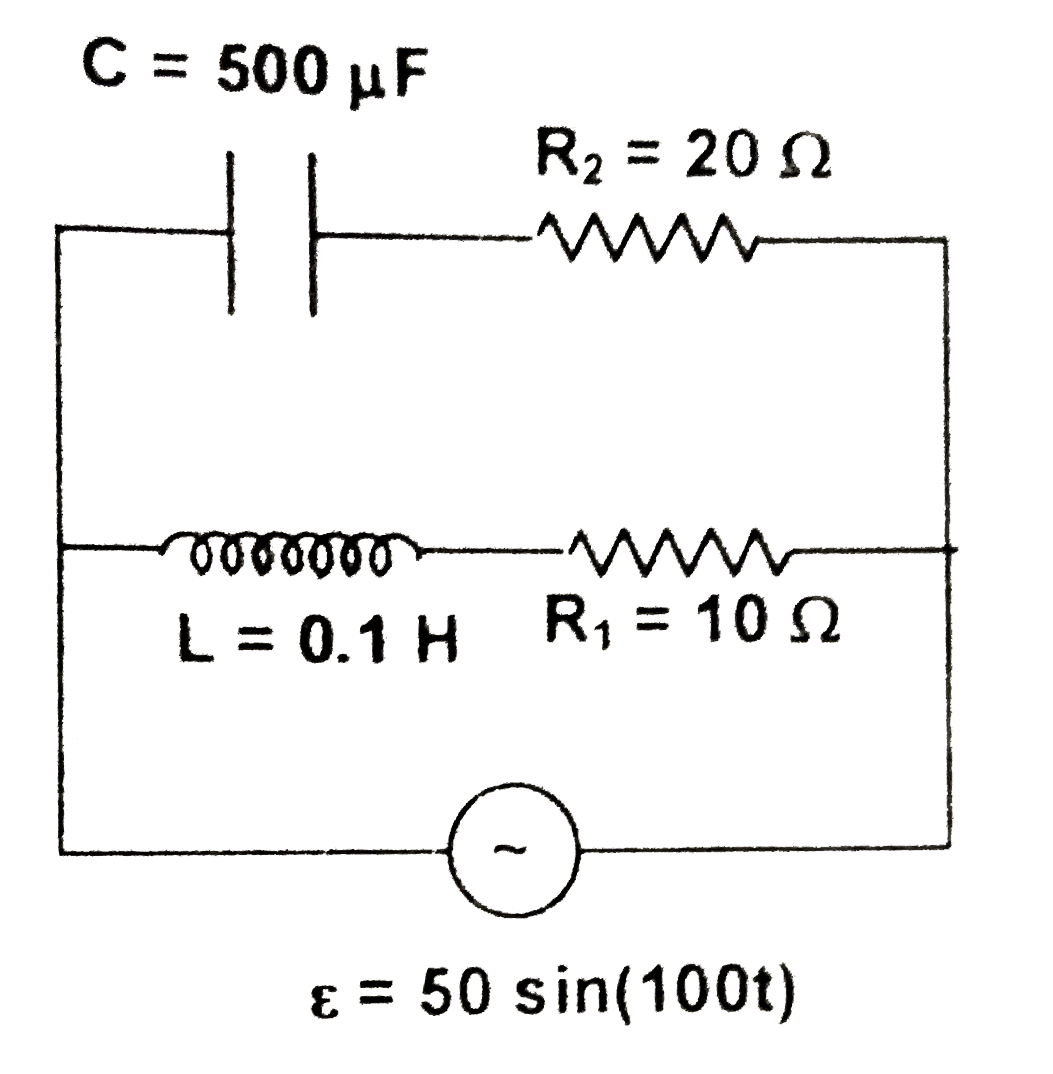
In the circuit shown the average power developed in the resistor R1 isA31.25 WB62.50 WC125 WD250 WIn the given circuit the power dissipated through resistance R1=9Ω is P1, when switch S1 is closed and S2 is opened and the power dissipated through resistance R2=4Ω is P2, when switch S2 is closed and S1 is opened. If P1=P2, then r is equl to :
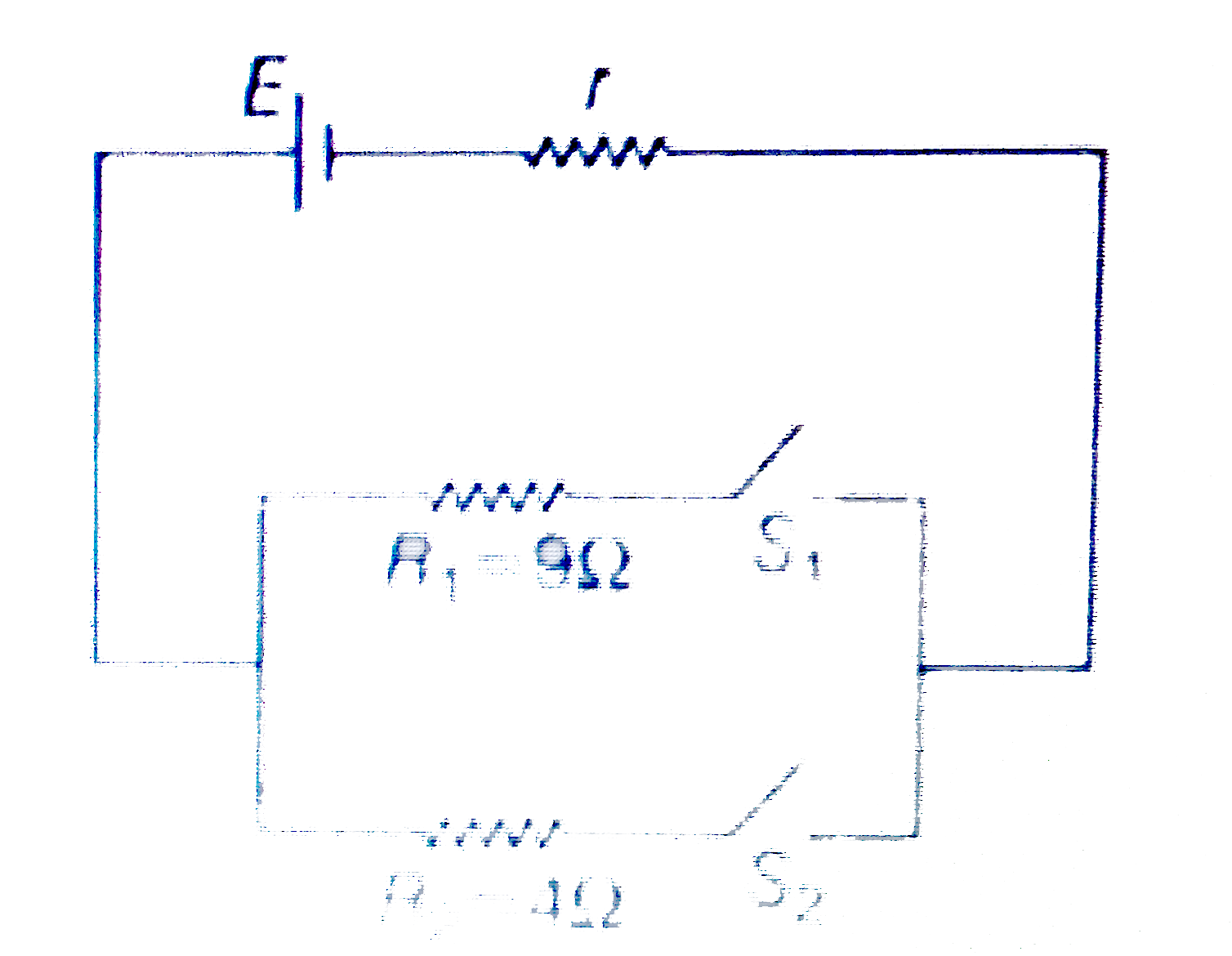 A2ΩB6ΩC4ΩD3Ω
A2ΩB6ΩC4ΩD3ΩFind the RAB in the given network.
 A5 ohmsB10 ohmsC2 ohmD2/3 ohm
A5 ohmsB10 ohmsC2 ohmD2/3 ohm
The current is drawn from a cell of emf E and iternal resitance r connected to the network of resistors each of resistor r as shown in the figure. Obtain the expression for (i) the current draw from the cell and (ii) the power consumed in the network.
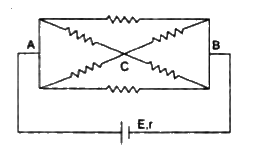
View SolutionIn the figure shown, a conducting wire PQ of length l=1m, is moved in a uniform magnetic field B=4T with constant velocity v=2m/s towards right. Given R=2Ω,C=1FandL=4H.

Currents through resistor, capacitor and inductor at any time t are l1,I2andI3 respectively. Current through wire PQ is I.
At t=2s, suppose P is the initial power generated by the applied force. P1 the power generated by the applied for, P1 the power stored in magnetic field of inductor and P2 the power dissipated in resistance. The
View SolutionA resistor R1 dissipates the power P when connected to a certain generator. If the resistor R2 is put in series with R1, the power dissipated by R1
View SolutionA resistor R1 dissipates the power P when connected to a certain generator. If the resistor R2 is put in series with R1, the power dissipated by R1
View SolutionA network of four unequal resistor R1,R2,R3 and R4 are connected in a network (see diagram) that contains a source of e.m.f E and an ammeter A. The source has negligible internal resistance. For this network,
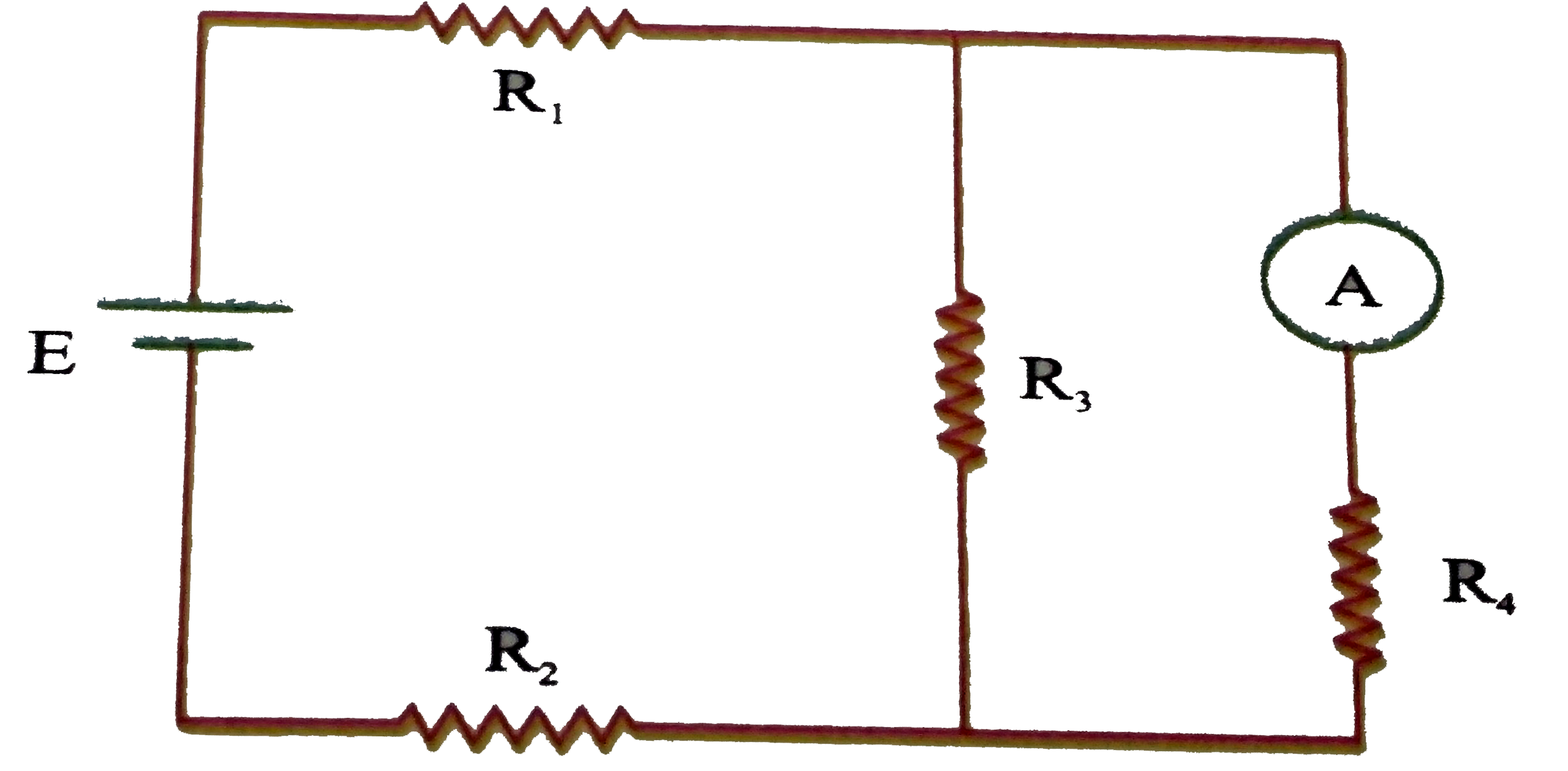
View Solution