A meter scale of mass is lying horizontally on the floor. If it is to be held vertically with one end touching the floor, the work to be done is
The correct Answer is:D
To solve the problem of calculating the work done to lift a meter scale from a horizontal position to a vertical position, we can follow these steps:
1. Identify the Mass and Length of the Scale:
- The mass of the meter scale is given as m=400g=0.4kg.
- The length of the scale is L=1m.
2. Determine the Initial Position of the Center of Mass:
- When the scale is lying horizontally, the center of mass is at the midpoint of the scale.
- Therefore, the initial height of the center of mass is:
hi=0m
3. Determine the Final Position of the Center of Mass:
- When the scale is held vertically, the center of mass is still at the midpoint, but now it is raised to a height of:
hf=L2=1m2=0.5m
4. Calculate the Change in Height:
- The change in height (Δh) of the center of mass when moving from the initial position to the final position is:
Δh=hf−hi=0.5m−0m=0.5m
5. Calculate the Work Done Against Gravity:
- The work done against gravity can be calculated using the formula for gravitational potential energy:
W=mgh
- Substituting the values:
W=(0.4kg)×(9.8m/s2)×(0.5m)
- Calculating this gives:
W=0.4×9.8×0.5=1.96J
6. Final Answer:
- The work done to lift the meter scale from a horizontal position to a vertical position is approximately:
W≈2J(rounding to two significant figures)
- The mass of the meter scale is given as m=400g=0.4kg.
- The length of the scale is L=1m.
- When the scale is lying horizontally, the center of mass is at the midpoint of the scale.
- Therefore, the initial height of the center of mass is:
hi=0m
- When the scale is held vertically, the center of mass is still at the midpoint, but now it is raised to a height of:
hf=L2=1m2=0.5m
- The change in height (Δh) of the center of mass when moving from the initial position to the final position is:
Δh=hf−hi=0.5m−0m=0.5m
- The work done against gravity can be calculated using the formula for gravitational potential energy:
W=mgh
- Substituting the values:
W=(0.4kg)×(9.8m/s2)×(0.5m)
- Calculating this gives:
W=0.4×9.8×0.5=1.96J
- The work done to lift the meter scale from a horizontal position to a vertical position is approximately:
W≈2J(rounding to two significant figures)
Topper's Solved these Questions
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-II (H.W)
Explore 54 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Subjective type Questions
Explore 9 Videos
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:LEVEL II(H.W)
Explore 51 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
Similar Questions
A uniform rod of length 4 m and mass 20 kg is lying horizontal on the ground. The work done in keeping it vertical with one of its ends touching the ground, will be -
View SolutionA plate of mass m, length b, and breadth a is initially lying on a horizontal floor with length parallel to the floor and breath perpendicular to the floor. Find the work done to erect it on its breadth.
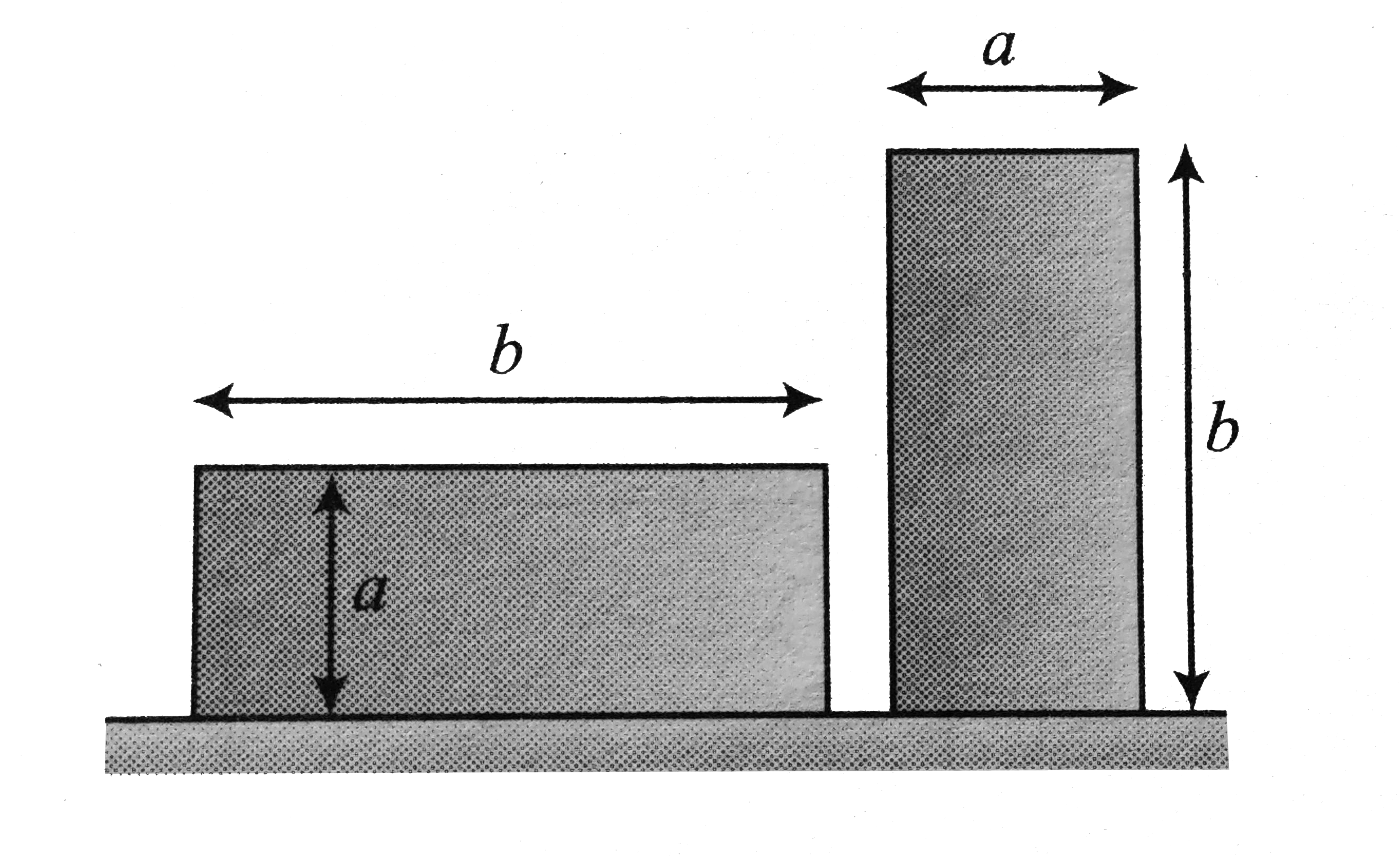
View Solution
Knowledge Check
A bicycle chain of length 1.6m and of mass 1kg is lying on a horizontal floor. If g=10ms−2, the work done in lifting it with one end touching the floor and the other end 1.6m above the floor is
A10JB3.2JC8JD16JA metre scale of mass 200 g, is lying on a horizontal table. What is the work done by student in making it stand vertically on one of its ends?
A2JB1.5JC1JD2.5Jn' identical cubes each of mass 'm' and edge 'L' are on a floor. If the cubes are to be arranged one over the other in a vertical stack, the work to be done is
ALmng(n−1)/2BLg(n−1)/mnC(n−1)/LmngDLmng/2(n−1)
A ladder of mass 10 kg is resting with its top end touching a vertical wall and the bottom end on the floor. If the angle between the ground and the ladder is 45°, find the horizontal force required at the bottom to prevent the ladder from sliding. Neglect friction and take g=10ms−2.
View SolutionThe one end of a 20 m long ladder is on the floor and the other end is in the contact of vertical wall. Its lower end slides on the floor. Show that the rate of sliding of the upper end is 4/3 times the rate of sliding the lower end when the lower end is 16 m away from the wall.
View SolutionA stone of mass l kg is lying on the floor of a train which is accelerating with 1ms−2 The net force acting on the stone is
View SolutionA meter stick is hold vertically with one end on the floor of the sticks does not move. The velocity of the other end when it hits the floor, will be
View SolutionA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View Solution