A particle P of mass m is attached to a vertical axis by two strings AP and BP of legth l each. The separation AB=l, rotates around the axis with an angular velocity ω. The tension in the two string are T1 and T2. Then
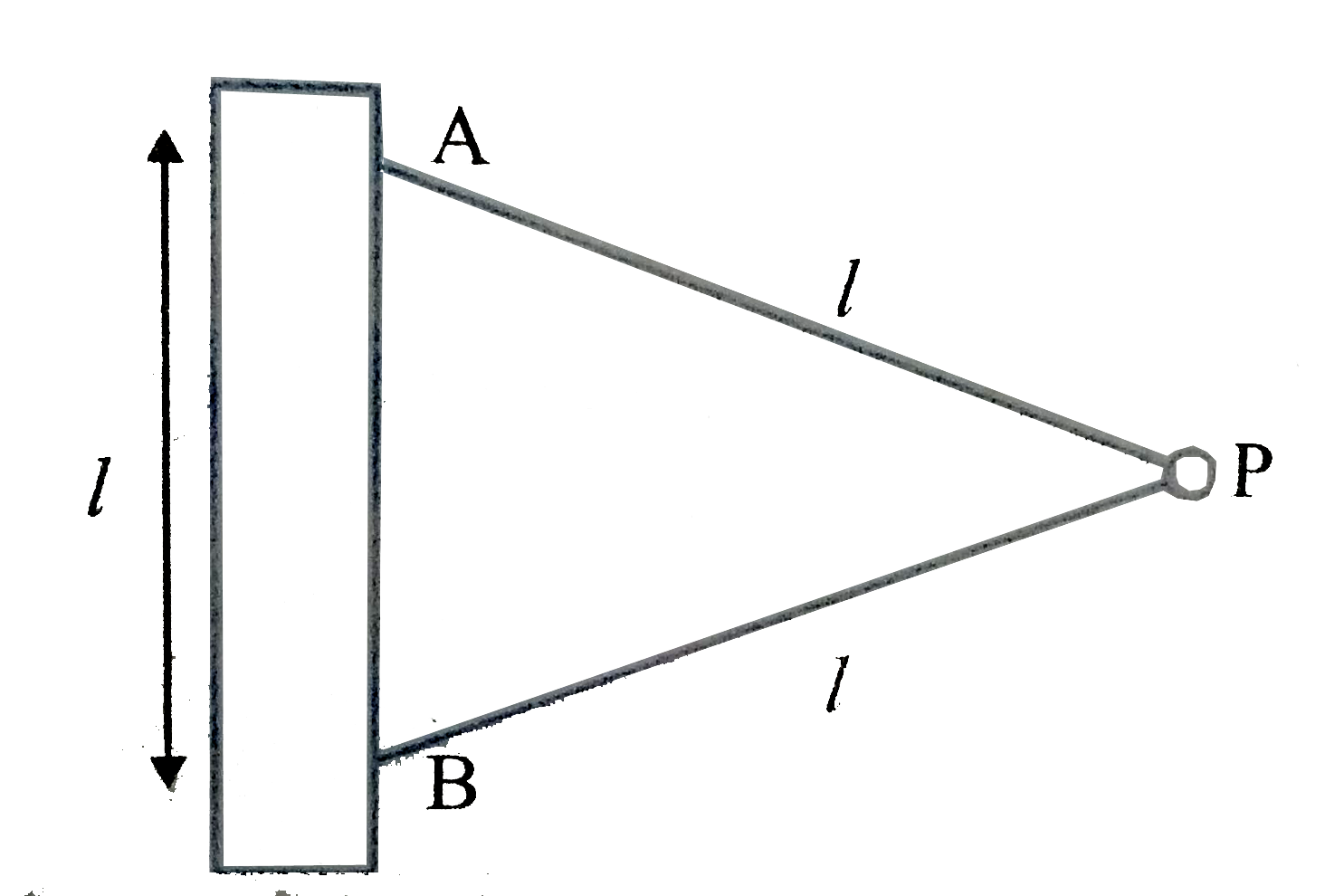
T1=T2
T1+T2=mω2l
T1−T2=2mg
BP will remains taut only if ω≥√2g/l
The correct Answer is:B, C, D
ABP equilateral, T(1),T2 tensions along PA and PB respectively
T1cos60=T2cos60+mg,T1−T2=2mg
T1sin60+T2sin60=g(lsin60)ω2
T1+T2=mω2l, if T2=0
T1=2mg,⇒ω2l=2g
if ω≥√2gl BP will be taut
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL-VI PASSAGE
3 Videos
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL-VI Integer
7 Videos
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)
51 Videos
- CALORIMETRYBOOK - NARAYNACHAPTER - CALORIMETRYEXERCISE - Level- II (H.W)
11 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-II (H.W)
54 Videos
Similar Questions
A ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionA particle of mass m is attached to a vertical rod with two inextensible strings AO and BO of equal lengths l. Distance between A and B is also l. The setup is rotated with angular speed ω with rod as the axis.
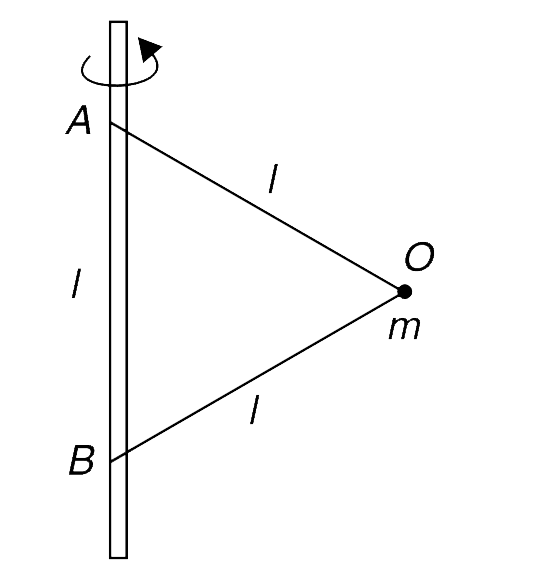
(a) Find the values of ω for which the particle remains at point B.
(b) Find the range of values of ω for which tension (T1) in the string AO is greater than mg but the other string remains slack
(c) Find the value of ω for which tension (T1) in string AO is twice the tension (T2) in string BO
(d) Assume that both strings are taut when the string AO breaks. What will be nature of path of the particle moment after AO breaks ?
View Solution
Knowledge Check
A particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity ω. The tensions in the two strings are T1andT2
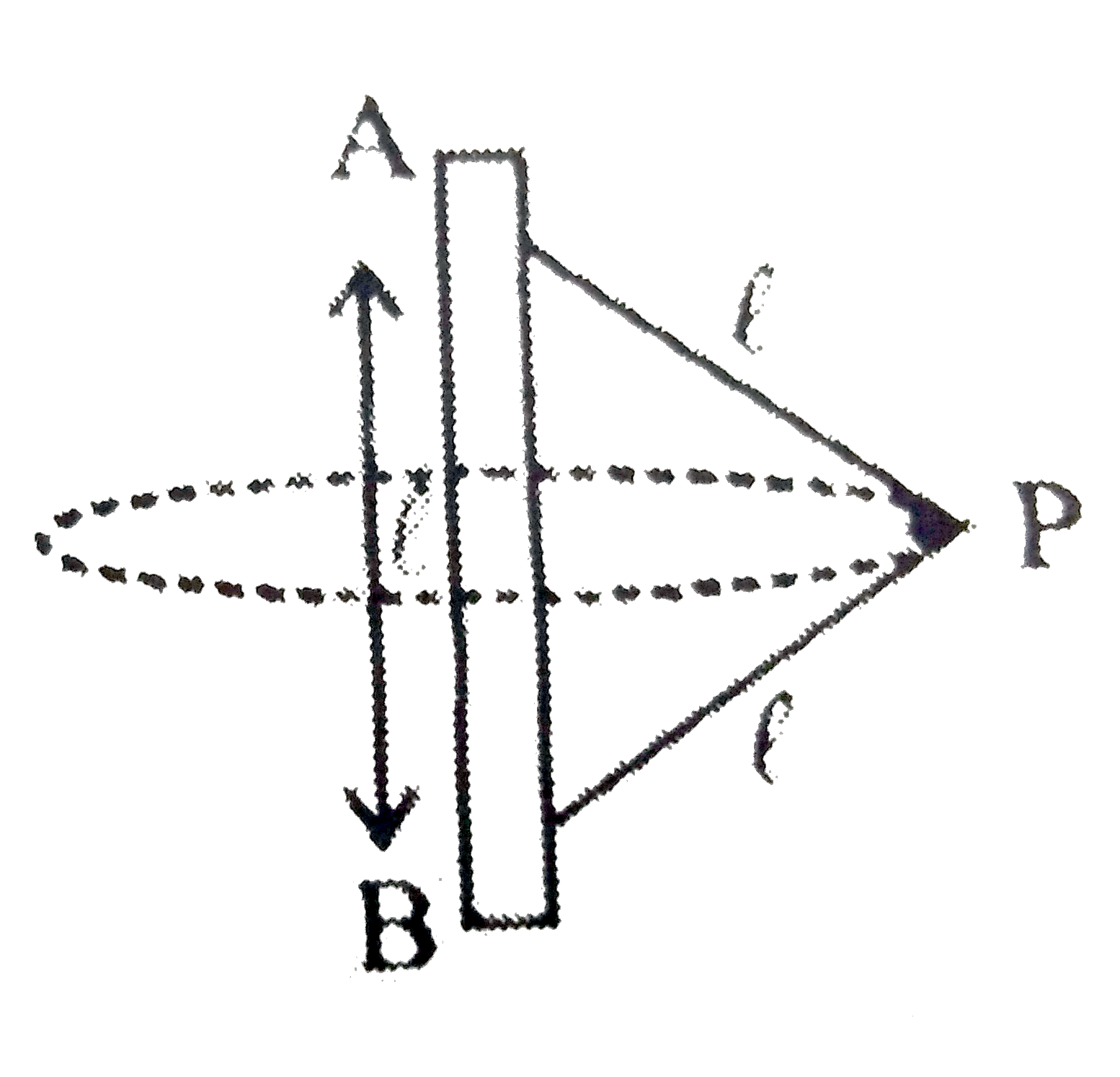 AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remain taut only if ω≥√2gl
AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remain taut only if ω≥√2glA particle A of mass m is attached to a vertical axis by two stings PA and QA of lengths 3L and 4L , respectively. PQ=5L. A rotates around the axis with an angular speed ω. The tension in the two strings are T1 and T2.
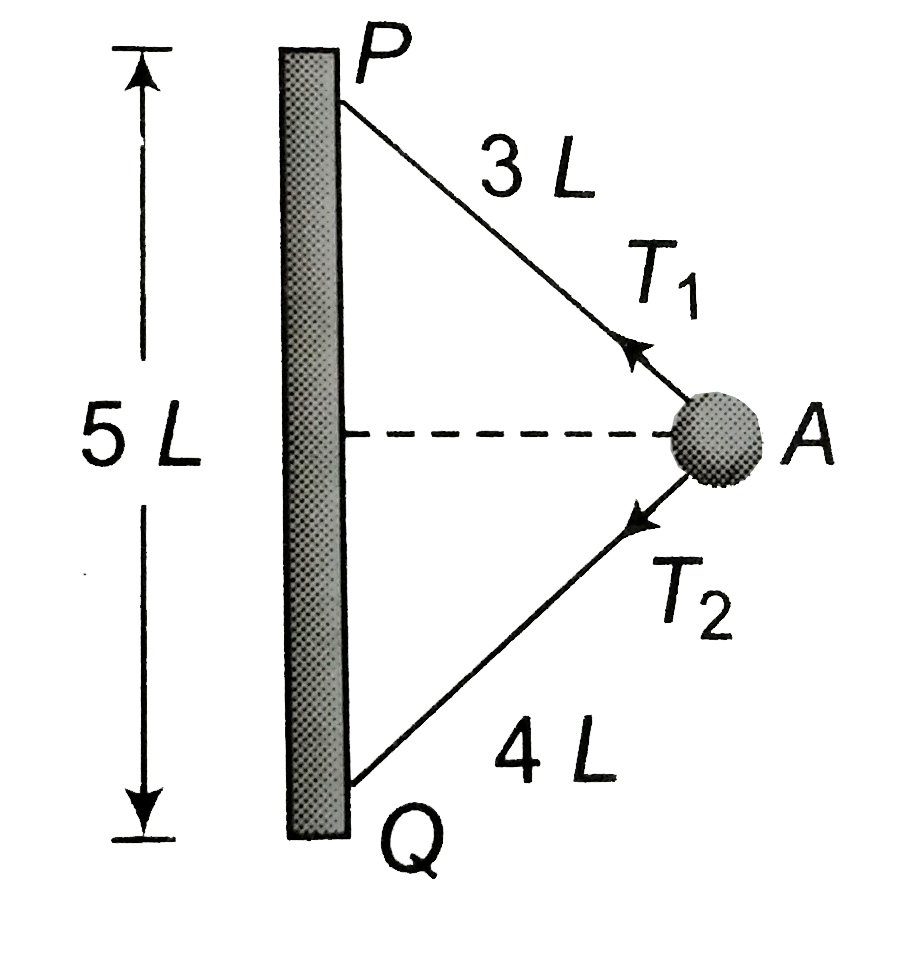
(i) T1=T2
(ii) 3T1−4T2=5mg
(iii) 4T1+3T2=12mω2LA(i)onlyB(i),(ii)C(i),(iii)D(ii),(iii)Two masses M and m are attached to a vertical axis by weightless threads of combined length l . They are set in rotational motion in a horizontal plane about this axis with constant angular velocity ω . If the tensions in the threads are the same during motion, the distance of M from the axis is
AMlM+mBmlM+mCM+mMlDM+mml
The particle P of mass m is attached to two light, rigid rods AP and BP of length l each. A and B are hings on a fixed vertical axis. The system APB can rotate freely about this axis. The angle ABP = the angle BAP=θ. The tensions in AP and BP are T1 and T2 respectively.
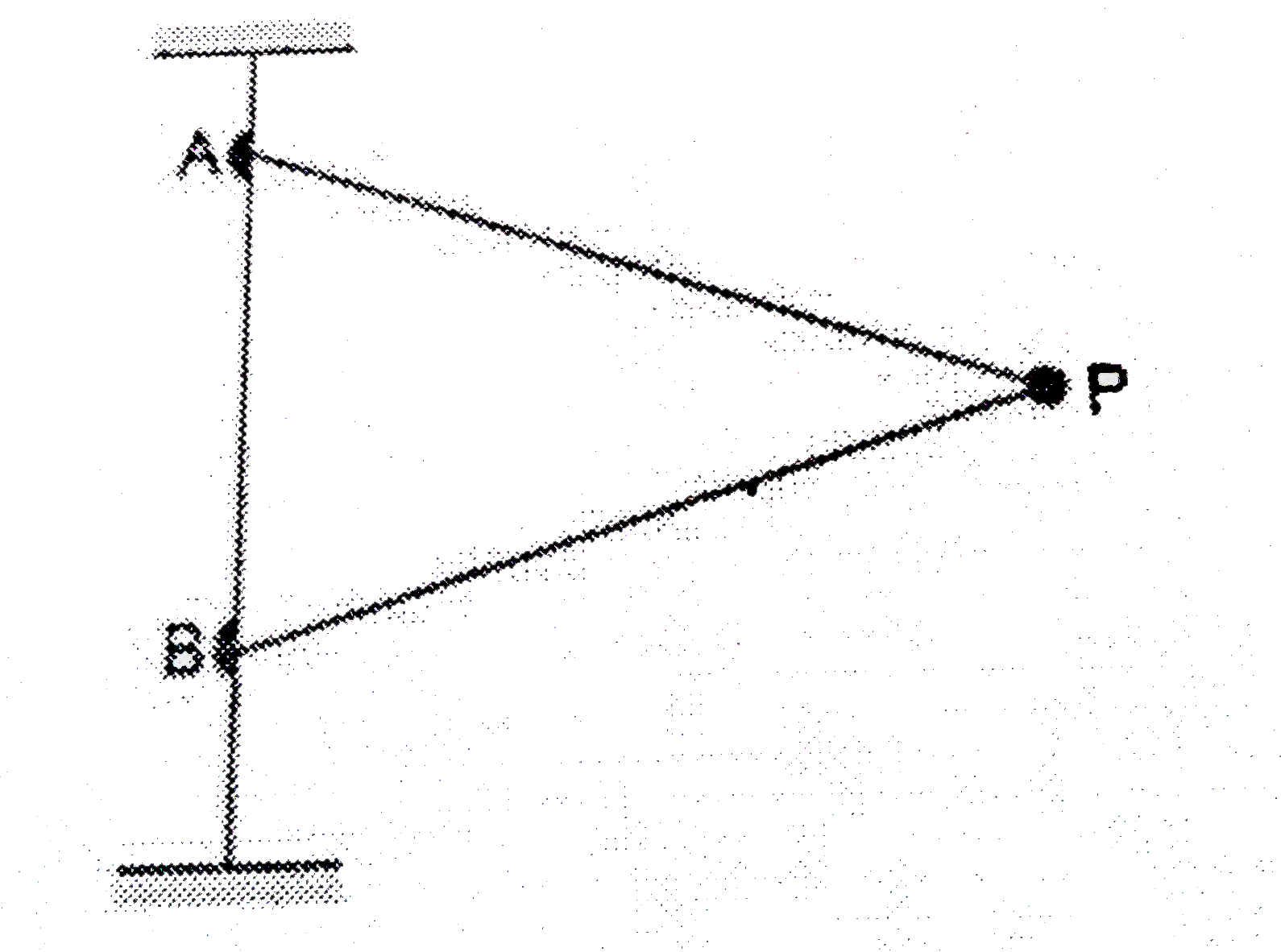
When the system is made to rotate about AB with angular velocity ω, which of the following is not correct?
View SolutionThe particle P of mass m is attached to two light, rigid rods AP and BP of length l each. A and B are hings on a fixed vertical axis. The system APB can rotate freely about this axis. The angle ABP = the angle BAP=θ. The tensions in AP and BP are T1 and T2 respectively.

The system is now rotated by 90∘ so that must be imparted to P, normal to the plane of the figure, such that it moves in a complete circular path in a vertical plane with AB as the axis?
View SolutionThe particle P of mass m is attached to two light, rigid rods AP and BP of length l each. A and B are hings on a fixed vertical axis. The system APB can rotate freely about this axis. The angle ABP = the angle BAP=θ. The tensions in AP and BP are T1 and T2 respectively.
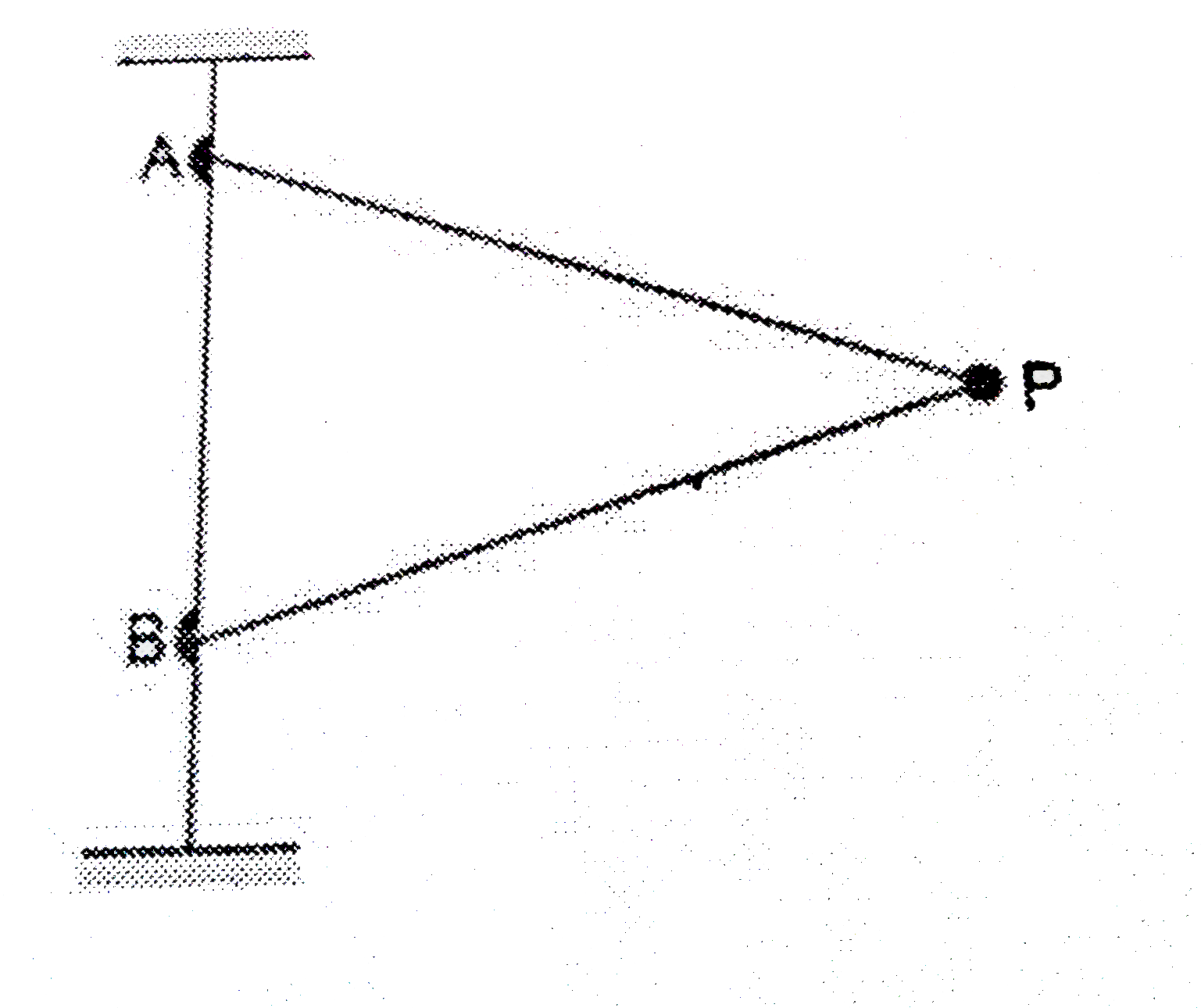
When the system is at rest, which of the following is not correct?
View SolutionA partical of mass m is attached to a massless string of length l and is oscillating in a vrtical plane with the other end of the string fixed to a rigid support. The tension in the string at a certain instant is T=kmg .
View SolutionTwo particles, each of mass m are attached to the two ends of a light string of length l which passes through a hole at the centre of a table. One particle describes a circle on the table with angular velocity ω1 and the other describes a circle as a conical pendulum with angular velocity ω2 below the table as shown in figure -3.86. if l1 and l2 are the lengths of the portion of the string above and below the table then :

View Solution
