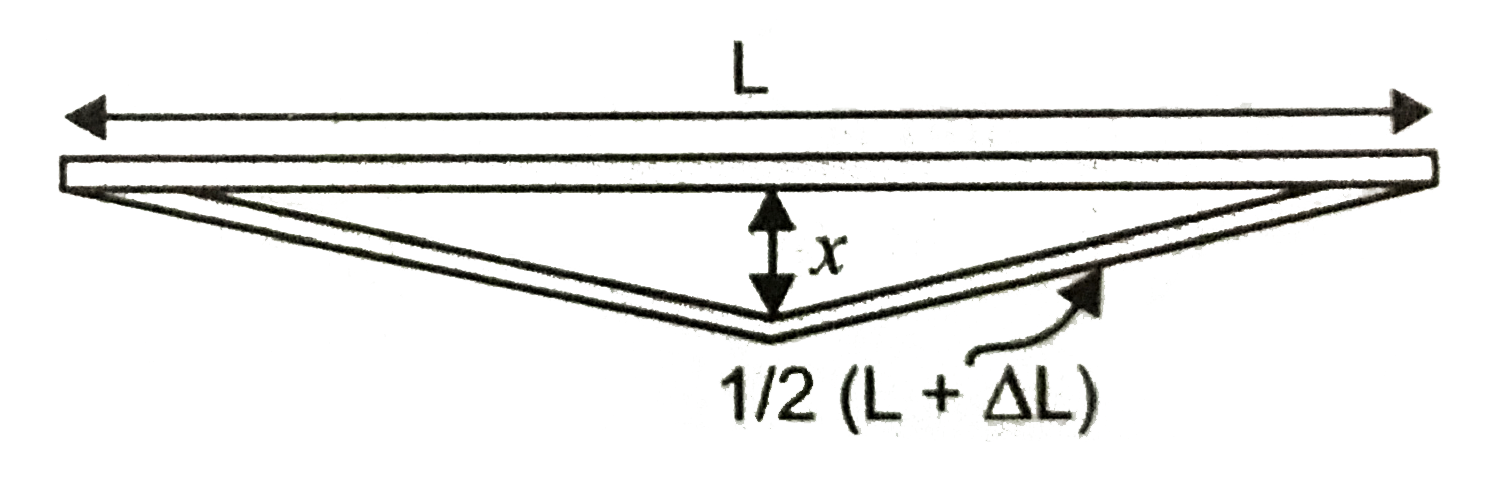
A steel rail 30m long is firmly attached to the road be only at its ends. The sun raises the temperature of the rail by 500C, causing the rail to buckle. Assuming that the buckled rail consitst of two straight parts metting in the centre, calculate how much the centre of the rail rise? Given, alpha_(steel) = 12 xx 10^(-6//@)C.
_S01_024_Q01.png)
Let the initial length be 2x and the final total length be 2(x+Δx) as shown.
Let y be the height of the centre of the buckled rail Clearly, Δx=αxΔT and
y=√(x+Δx)2−x2=√2x(Δx)=√2x2αΔt
y=x√2αΔT[neglecting(Δx)2]
Thus, y=[15√2(12×10−6)50]cm=0.52m
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL-III
22 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL-I (C.W.)
23 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL-I(H.W.)
21 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
- THERMODYNAMICSBOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise
187 Videos
Similar Questions
A steel rail 30 m long is firmly attached to the roadbed only at its ends. The sun raises the temperature of the rail by 5∘C, causing the rail to buckle. Assuming that the buckled rail consists of two straight parts meeting in the centre, calculate how much the centre of the rail rises. coefficient of linear expansion of steel is 12×10−6/K.
View SolutionA rail track made of steel having length 10 m is clamped on a railway line at its two ends
on a summer day due to rise in temperature by 20∘C, it is deformed as shown in fig. Find x (displacement of the centre) if αsteel=1.2×10−5/∘C.
View Solution
Knowledge Check
A second's pendulum clock havig steeel wire is calibrated at 20∘C. When temperature is increased to 30∘C, then calculate how much time does the clock
[αSteel=1.2×10−6∘C−1A0.3628 sB3.626 sC362.8 sD36.23 sA heavy brass bar has projections at its ends as shown in the figure. Two find steel wires, fastened between the projections, are just taut (zero tension) when the whole systeam is at 00C. What is the tensile stress in the steel wires when the temperature of the systeam is raised to 3000C?
Given that
αbrass=20×10−6∘C−1
αsteel=12×10−6∘C−1Ysteel=2×1011Nm−2
_E01_077_Q01.png)
A48×107Nm−2B84×107Nm−2C32×104Nm−2D24×104Nm−2A rail track made of steel having length 10m is clamped on a railway line at its two end (figure). On a summer day due to rise in temperatue by 20∘C. It is deformed as shown in figure. Find x (displacement of the centre) if αsteel=1.2×10−5/∘C
A15√30×10−3cmB10√30×10−3cmC25√30×10−3cmD20√30×10−3cm
Gaps are left while laying the railway lines in order to allow for expansion. The gap between steel rails of length 65 m is 3.56 cm at 15∘C . Calculate the temperature at which the rails will just touch each other. Take, Osteel=1.1×10−5∘C−1
View SolutionTwo straight conducting rails from a right angle where their end are joined. A conducting bar polaced over the rails starts at vertex at the time t=0 and moves with a constant velocity v to the right as shown in the figure. Calculate
(a) the flux through the triangle (isosceles) by the rails and bar at t=t0
the emf around the triangle at that time
(c) in what manner does the emf around the triangle vary with time
View SolutionA bar with a crack at its centre buckles as a result of temperature rise of 32∘C. If the fixed distacne L0 is 3.77 m and the coefficient of linear expansion of the bar is 25×106/∘C find the rise (in metre) of the centre.
View SolutionAssume that one early morning when the temperature is 10∘C a driver of an automobile gets his gasoline tank which is made of steel, filled with 75 L of gasoline, which is also at 10∘C Durign the day, the temperature rises at 30∘C how much gasoline will overflow ?
(Given, α for steel = 1.2×10−5∘C−1,γ for gasoline =9.5×10−4∘C)
View SolutionTwo straight thin bars, one of brass and the other of steel are joined togethre side by side by short steel cross-pieces at 0∘C, one cm long the centre lines of the bars being one cm apart. When heated to 100∘C, the composite bar becomes bent into the arc of a circle. calculate the radius of this circle.
α for brass =19×10−6 per .∘C
and α for steel =11×10−6 per .∘C
View Solution