A rail track made of steel having length 10 m is clamped on a railway line at its two ends
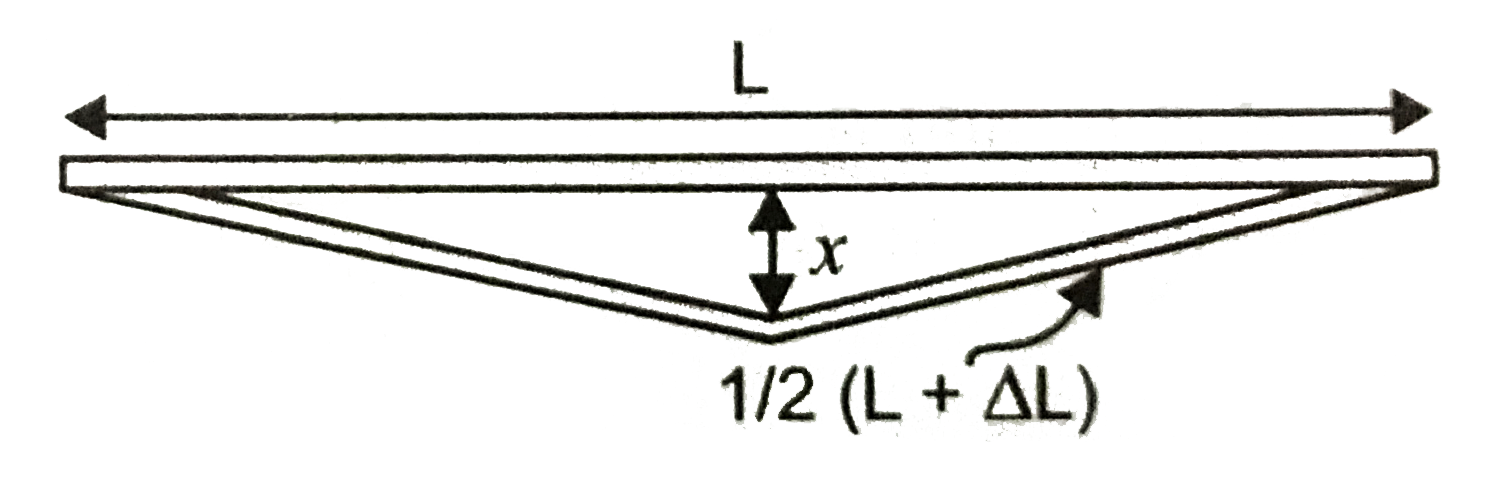
on a summer day due to rise in temperature by 20∘C, it is deformed as shown in fig. Find x (displacement of the centre) if αsteel=1.2×10−5/∘C.
From the given fing
x=√(L+ΔL2)2−(L2)2=12√(L+ΔL)2−L2=12[ΔL2+2LΔL]1/2 Since ΔL is a small quantity the term wich ΔL2 being very small can be neglected. ∴X=12[2LΔL]1/2
Now ΔL=LαΔθ
x=12[2L×LαΔθ]1/2=102[2×(1.2×10−5)×20]1/2=10[1.2×10−4]1/2
=10×10−2×1.1m≈0.11m
Similar Questions
A rail track made of steel having 20m is clamped on a railway line at its two ends as show in Fig. 7(d).17. On a summer day due to rise in temperature by 22∘C, it is deformed as show in Fig. 7(d).17 .Find displacement of the center (x) . Given cofficient of liner expansion of steel is 1.2×10−5.∘C−1.

View SolutionA steel tape is correctly calibrated at 20∘C and is used to measure the length of a table at 30∘C. Find the percentage error in the measurement of length. [αsteel=11×10−5/.∘C]
View Solution
Knowledge Check
A rail track made of steel having length 10m is clamped on a railway line at its two end (figure). On a summer day due to rise in temperatue by 20∘C. It is deformed as shown in figure. Find x (displacement of the centre) if αsteel=1.2×10−5/∘C
 A15√30×10−3cmB10√30×10−3cmC25√30×10−3cmD20√30×10−3cm
A15√30×10−3cmB10√30×10−3cmC25√30×10−3cmD20√30×10−3cmA steel wire of length 1m and mass 0.1kg and having a uniform cross-sectional area of 10−6m2 is rigidly fixed at both ends. The temperature of the wire is lowered by 20∘C. If the wire is vibrating in fundamental mode, find the frequency (in Hz). (Ysteel=2×1011N/m2,αsteel=1.21×10−5/.∘C).
A11B20C15D10A rod has been laid by using alternate rails of steel and aluminium each 12m long in a winter season when temperature is .−2∘C. The maximum temprature which can must be left be-tween advance rules of they are just to touch on a summer day
(αsteel=1.2×10−5^(0)C−1αAl=2.4×10−5^(0)C−1A0.6cmB1.2cmC0.95cmD0.86cm
The scale on a steel on a steel meter stick is calibrated at 15∘C. What is the error in the reading of 60cm at 27∘C ? αsteel=1.2×10−5(.∘C)−1.
View SolutionA concrete slab has a length of 10 m on a winter night when the temperature is 0C. Find the lenth of the slab on a summer day when the temperature is 35C. The coefficient of linear expansion of concrete is 1.0XX10−50C^(−1).
View SolutionA gasoline tank made of steel is filled completely with 60 litres of gasoline, both at a temperature of 12∘C . How much gasoline will overflow when the temperature is increased to 25∘C ?
αsteel=1.1×10−5∘C−1
γgasoline=9.5×10−4∘C−1
View SolutionA surveryor uses a steel measuring tape that is exactly 50.000 m long at a temperature of 20∘C
What is its length on a hot summer day when the temperature is 35∘C? (αstell=1.2×10−5K−1)
View SolutionA horizontal steel railroad track has a length of 100 m when the temperature is 25∘C. The track is constrained from expanding or bending. The stress on the strack on a hot summer day, when the temperature is 40∘C, is (Note : the linear coefficient of thermal expansion for steel is 1.1×10−5/.∘C and the Young's modulus of steel is 2×1011 Pa)
View Solution