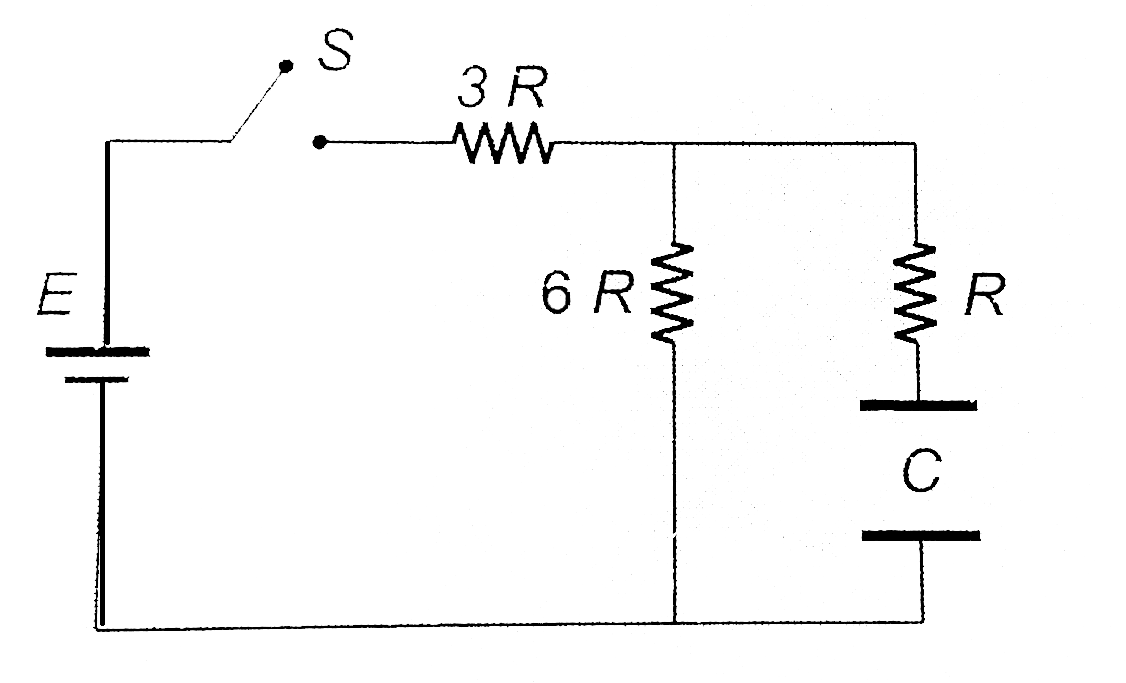
Find (a) equivalent time constant, (b) charge on capacitor in terms of time t.
First find equivalent resistance across capacitor after short circuiting the battery
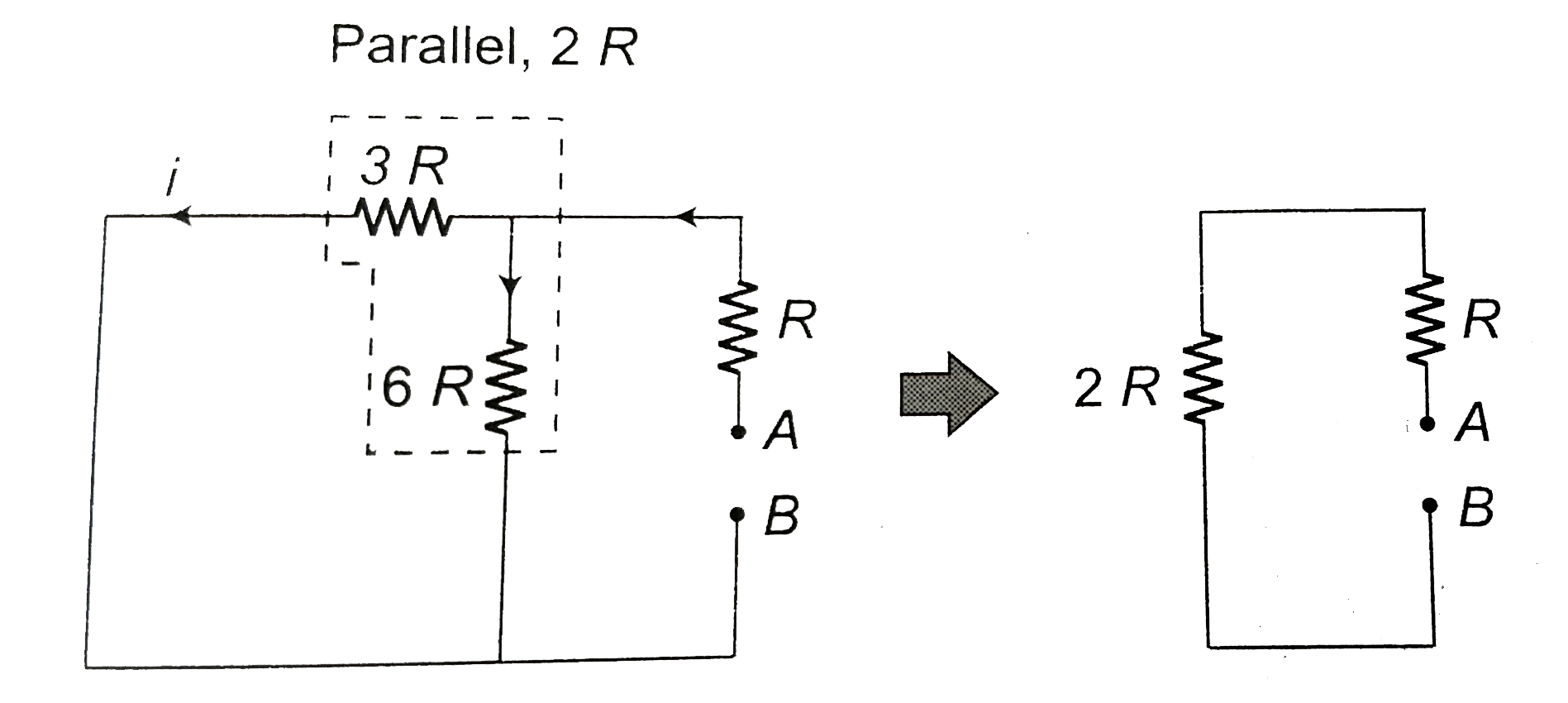
Equivalent resistance between A and B or across capacitor
Req=2R+R=3R
Time constant τ=ReqC=3RC
(b) Charge on capacitor in steady state, capacitor offers infinite resistance.
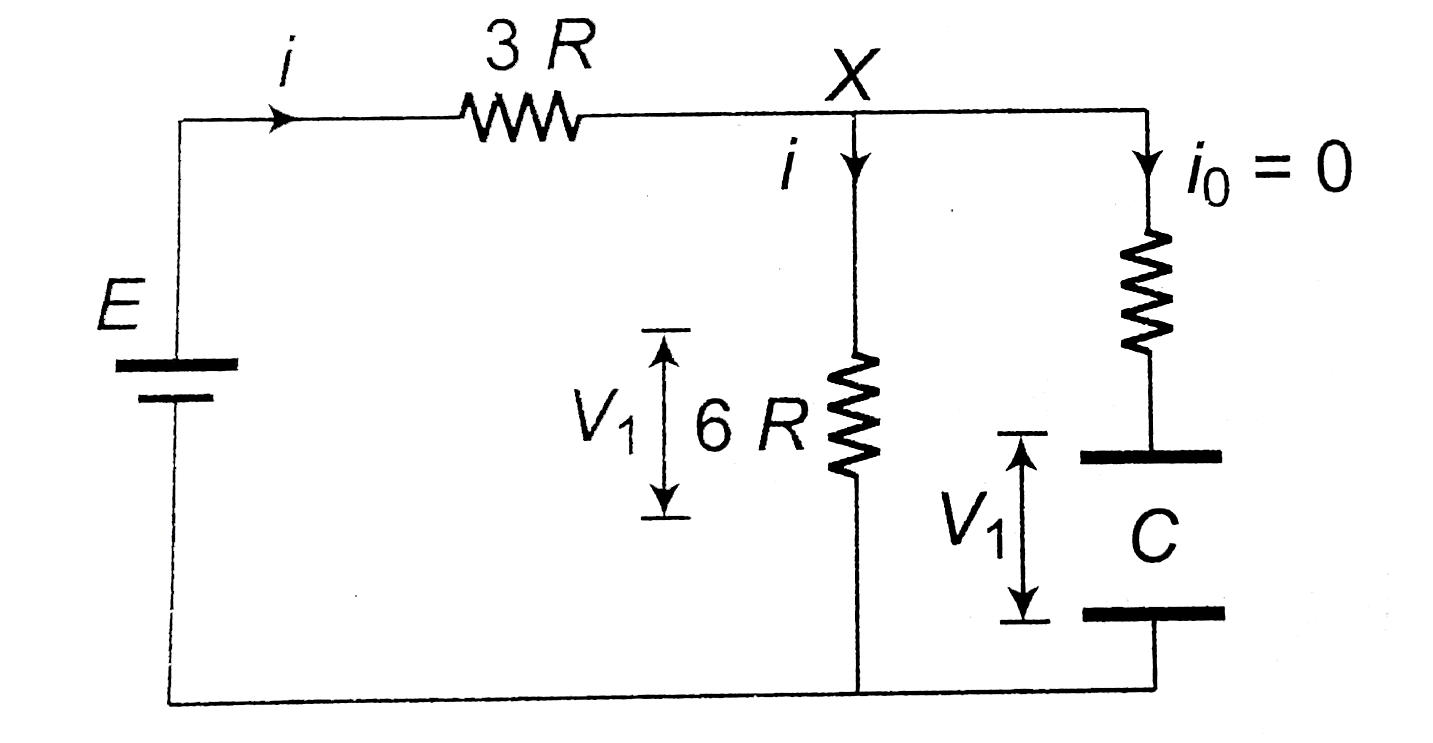
V1=6R3R+6RE=2E3
Charge on capacitor
q0=CV1=2CE3
Hence charge on capacitor at any time t
q=q0(1−e−t/τ)
=2CE3(1−e−t/3RC).
Topper's Solved these Questions
- THERMAL AND ELECTRIC EFFECT oF CURRENTBook:CP SINGHChapter:THERMAL AND ELECTRIC EFFECT oF CURRENTExercise:Exercises
Explore 101 Videos
- SEMICONDUCTORSBook:CP SINGHChapter:SEMICONDUCTORSExercise:Exercises
Explore 140 Videos
- WAVE NATURE OF LIGHTBook:CP SINGHChapter:WAVE NATURE OF LIGHTExercise:EXERCISES
Explore 140 Videos
Similar Questions
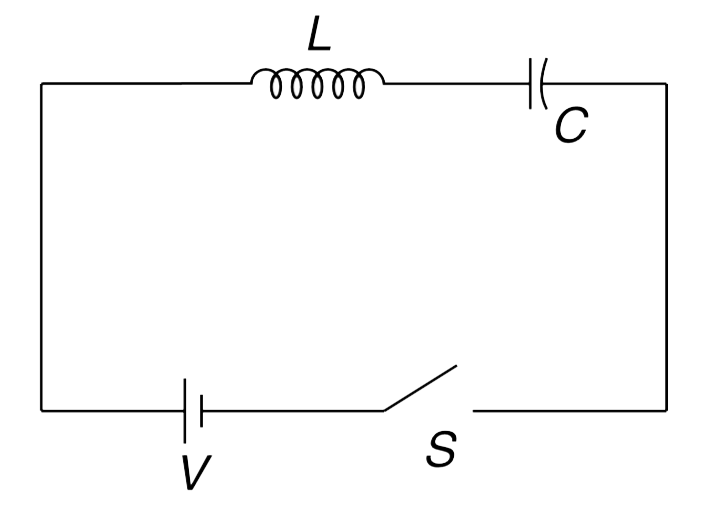
In the circuit shown in the figure, switch S is closed at time t=0.
(a) Write current in the circuit and charge on capacitor as a function of time. Draw the graphical plot for the same.
(b) Find maximum charge on the capacitor. What is potential difference across the inductor when charge on the capacitor is maximum?
View Solution" Time constant of charging of capacitor is equal to "(30.8)/(N)C" .Find "N
View Solution
Knowledge Check
In the circuit shown in figure find

a. the equivalent capacitance
b. the charge stored in each capacitor and
c. the potential difference across each capacitor.A1.2μF 120μC 60Vand40VB1.2μF 120μC 60Vand20VC1.2μF 12μC 60Vand40VD12μF 120μC 60Vand40V
A capacitor of capacity 1μF is connected in a closed series circuit with a resistance or 107 ohms, an open key and a cell of 2 V with negligible internal resistance :
(i) When the key is switched on at time t=0, find,
(a) The time constant for the circuit.
(b) The charge on the capacitor at steady state.
(c) Time taken to deposit charge equal to half of charge that will deposit at steady state.
(ii) If after completely charging the capacitor, the cell is shorted by zero resistance at time t=0, find the charge on the capacitor at t=50 s. (Given : e−5=6.73×10−3,ln2=0.693)
View Solution(a) The amount of charge passed in time t through a cross-section of wire is
q=αt−βt2
where α and β are constant.
(i) Find current in terms of time t.
(ii) Sketch i versus t graph.
(b) The current through a wire depends on time as
i=4+3t+2t2
Find the charge crossed through a section of wire in 6sec.
View SolutionIn figure the battery has a potential difference of 20V. Find
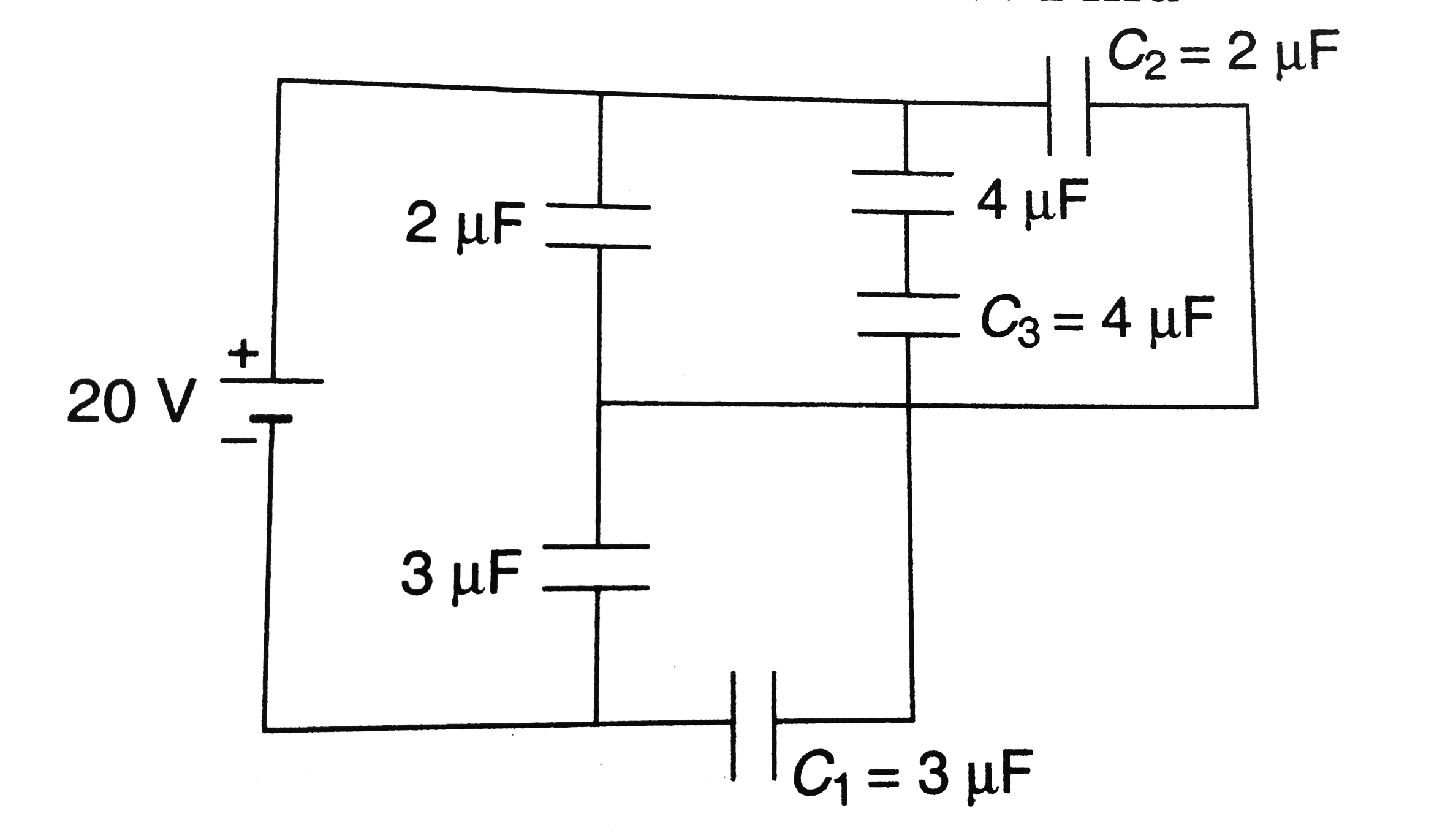
(a) the equivalent capacitance of all the capacitors across the battery and
(b) the charge stored on that, equivalent capacitance. Find the charge on
(c) capacitor 1,
(d) capacitor 2, and
(e) capacitor 3.
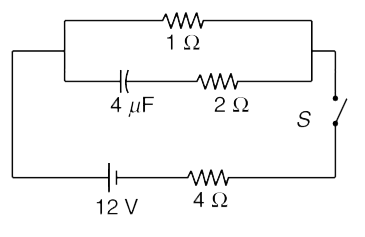
View SolutionIn the circuit shown in the figure, switch S is closed at time t=0. Charge on positive plate of capacitor is q at time t.
(a) Derive a differential equation for q at time t.
(b) Solve the equation to write q as a function of time.
(c) Put t = 0 and t=∞ in your equation to get charge on the capacitor at these times.
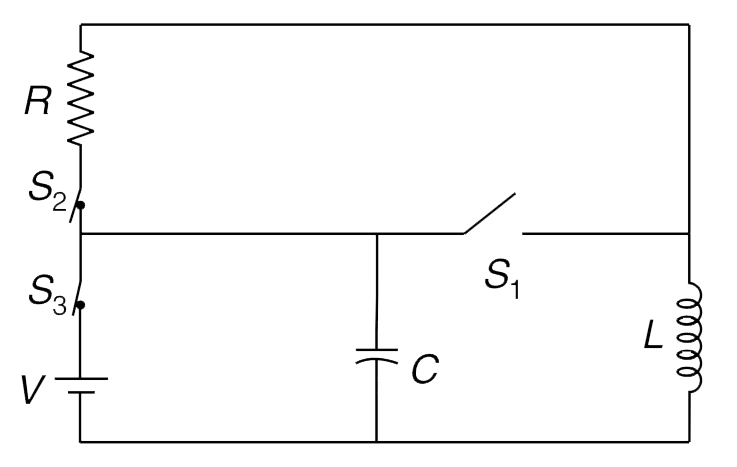
View SolutionIn the circuit shown in figure S1 is open and, S2 and S3 are closed. The circuit is in steady state. At time t = 0, switch S1 is closed and S2 and S3 are opened simultaneously. V=100volt,R=10Ω,C=100μF,L=0.03H
(a) Find the maximum charge that will appear on the capacitor at any time.
(b) Find the time at which the charge on the capacitor will become zero for the first time.
View SolutionIn the circuit shown in Figure, the battery is an ideal one, with emf V. The capacitor is initially uncharged. The switch S is closed at time t = 0 .
(a) Find the charge Q on the capacitor at time t.
(b) Find the current in AB at time t. What is its liniting value as t→∞:
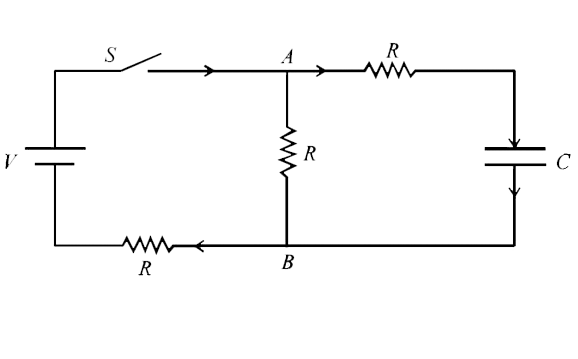 .
.
View SolutionWithout using the formula of equivalent. Find out charge on capacitor and current in all the branches as a function of time.
View Solution

