Two resistances , connected in parallel across a source of negligible interna resistance, consumes four times the power that they would consume when connected in series across the same source. If one of the resistances is 10Ω the other is
5Ω
10Ω
20Ω
40Ω
The correct Answer is:B
To solve the problem, we need to find the value of the second resistance when two resistances are connected in parallel and consume four times the power compared to when they are connected in series. Given that one of the resistances, R1, is 10Ω, we need to find the value of the other resistance, R2.
1. Understanding Power in Series and Parallel:
- When resistances are connected in series, the total resistance Rs is given by:
Rs=R1+R2
- The power consumed in series Ps is given by:
Ps=V2Rs=V2R1+R2
2. Power in Parallel:
- When resistances are connected in parallel, the total resistance Rp is given by:
Rp=R1R2R1+R2
- The power consumed in parallel Pp is given by:
Pp=V2Rp=V2(R1+R2)R1R2
3. Setting Up the Equation:
- According to the problem, the power consumed in parallel is four times that in series:
Pp=4Ps
- Substituting the expressions for Pp and Ps:
V2(R1+R2)R1R2=4⋅V2R1+R2
4. Canceling V2:
- Since V2 is common on both sides, we can cancel it out:
R1+R2R1R2=41
- This simplifies to:
R1+R2=4R1R2
5. Rearranging the Equation:
- Rearranging gives us:
R1+R2−4R1R2=0
6. Substituting Known Value:
- We know R1=10Ω:
10+R2−4(10)(R2)=0
- This simplifies to:
10+R2−40R2=0
- Combining like terms:
10−39R2=0
7. Solving for R2:
- Rearranging gives:
39R2=10
- Thus:
R2=1039≈0.256Ω
8. Conclusion:
- The other resistance R2 is approximately 0.256Ω.
- When resistances are connected in series, the total resistance Rs is given by:
Rs=R1+R2
- The power consumed in series Ps is given by:
Ps=V2Rs=V2R1+R2
- When resistances are connected in parallel, the total resistance Rp is given by:
Rp=R1R2R1+R2
- The power consumed in parallel Pp is given by:
Pp=V2Rp=V2(R1+R2)R1R2
- According to the problem, the power consumed in parallel is four times that in series:
Pp=4Ps
- Substituting the expressions for Pp and Ps:
V2(R1+R2)R1R2=4⋅V2R1+R2
- Since V2 is common on both sides, we can cancel it out:
R1+R2R1R2=41
- This simplifies to:
R1+R2=4R1R2
- Rearranging gives us:
R1+R2−4R1R2=0
- We know R1=10Ω:
10+R2−4(10)(R2)=0
- This simplifies to:
10+R2−40R2=0
- Combining like terms:
10−39R2=0
- Rearranging gives:
39R2=10
- Thus:
R2=1039≈0.256Ω
- The other resistance R2 is approximately 0.256Ω.
Topper's Solved these Questions
- THERMAL AND ELECTRIC EFFECT oF CURRENTBook:CP SINGHChapter:THERMAL AND ELECTRIC EFFECT oF CURRENTExercise:Exercises
Explore 101 Videos
- SEMICONDUCTORSBook:CP SINGHChapter:SEMICONDUCTORSExercise:Exercises
Explore 140 Videos
- WAVE NATURE OF LIGHTBook:CP SINGHChapter:WAVE NATURE OF LIGHTExercise:EXERCISES
Explore 140 Videos
Similar Questions
Three equal resistors connected in series across a source of emf together dissipate 10W of power. What would be the power dissipated if te same resistors are connected in parallel across the same source of emf?
View Solution(a) Two heater coils made of the same material are connected in paralled across the mains. The length of diameter of one the coil is triple that of other. Which of these will produce more heat?
(b) Three equal resistors connected in series across a source of emf together dissipated 10Wa of power. What would be the power disspated if the same resistors are connected in parallel across the same source of emf?
Two resistor R1 and R2 may be connect either in series or in parellel across a battery of zero internal resistance. it is required that joule heating for the parallel combination be four times than for series combination. if R1=100Ω find R2
(d) The three resistance A,BandC have values 3R,6R and R respectively. Now some potential difference is applied across the network . Find the ratio of thermal powers dissipated between X and Y . find ratio of power consumed by A,B,andC.
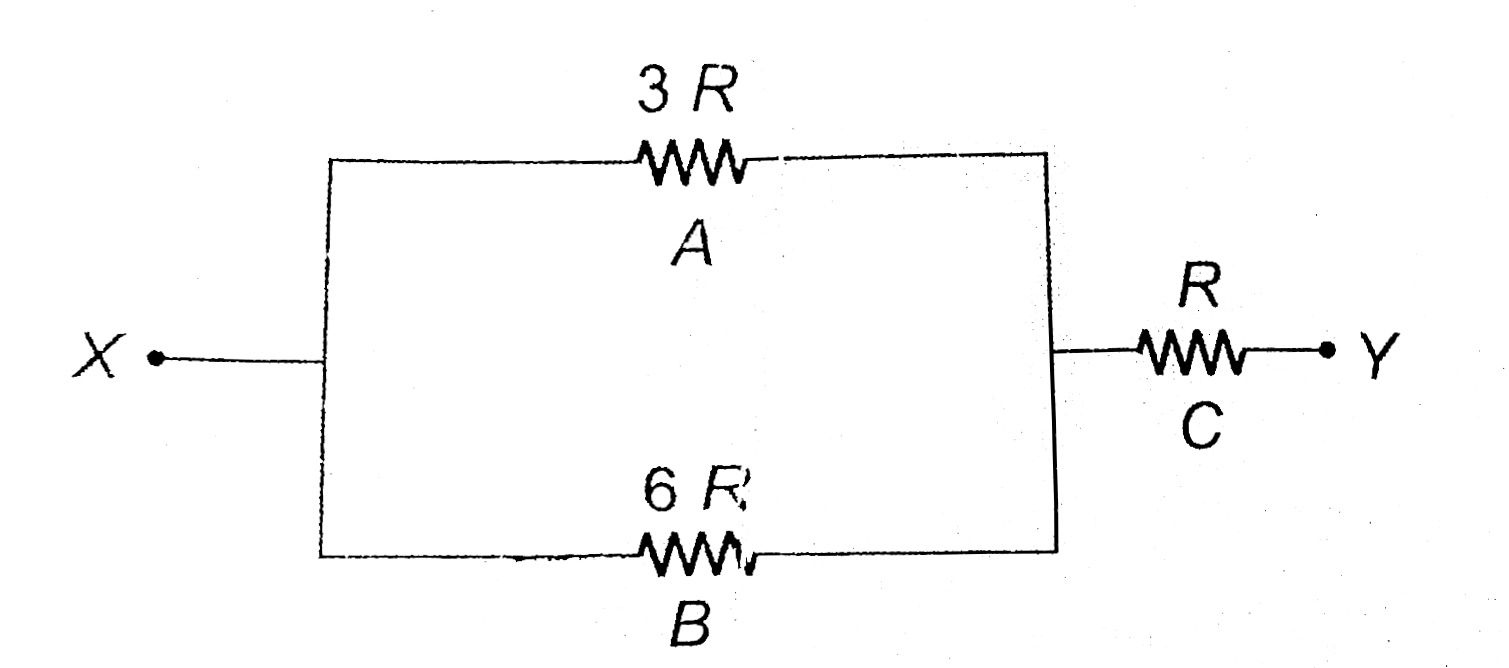
View Solution
Knowledge Check
Two resistance connected in parallel across a cell of negligible internal resistance, use 4.5 times the power that they would use, when in series across the same cell. If one of the resistance is 8ohm, the other is:-
A8ΩB12ΩC16ΩD36ΩThree equal resistors connected in series across a source of e.m.f. together dissipate 10 W of power. What should be the power dissipated if the same resistors are connected in parallel across the same source of e.m.f.
A9 WB90 WC10 WD100 WTwo equal resistances are connected in seires across a battery and consume a power P If these are connected in parallel, then power consumed will be
A4.0PB2.0CP2DP4
Three equal resistances connected is series across a source of e.m.f consume 20 watt. If the same resistor are connected in parallel across the same source of e.m.f., what would be the power dissipated ?
View SolutionA bulb of 40 W is connected across a source of 220 V . Find the resistance of the bulb.
View SolutionA voltmeter of resistance R1 and an ammeter of resistance R2 are connected in series across a battery oif negligible internal resistance. When as resistance R is connected in parallel to voltmeter reading of ammeter increases three times white that of voltmeter reduces to one third. Find R1 and R2 in terms of R.
View SolutionThree equal resistors connected in series across a source of emf together dissipate 10W of power. What would be the power dissipated if te same resistors are connected in parallel across the same source of emf?
View SolutionTwo bulbs when connected in parallel to a source take 60 W each, the power consumed, when they are connected in series with the same source is
View Solution

