Three equal resistors connected in series across a source of emf together dissipate 10W of power. What would be the power dissipated if te same resistors are connected in parallel across the same source of emf?
To solve the problem step by step, we will analyze the power dissipation in both series and parallel configurations of the resistors.
Step 1: Understand the Series Configuration
When three equal resistors (let's denote each resistor as R) are connected in series, the total resistance (R_total) is the sum of the individual resistances:
Rtotal=R+R+R=3R
Step 2: Power Dissipation in Series
The power (P) dissipated in a resistor can be calculated using the formula:
P=V2Rtotal
Given that the power dissipated in the series configuration is 10 W, we can write:
10=V23R
Step 3: Rearranging to Find V^2
From the equation above, we can rearrange it to find V2:
V2=10×3R=30R
Step 4: Understand the Parallel Configuration
Now, when the same resistors are connected in parallel, the equivalent resistance (R_eq) is given by:
1Req=1R+1R+1R=3R
Thus, the equivalent resistance is:
Req=R3
Step 5: Power Dissipation in Parallel
Using the same power formula for the parallel configuration, we have:
P′=V2Req
Substituting Req:
P′=V2R3=3V2R
Step 6: Substitute V^2 from Step 3
Now we can substitute V2 from Step 3 into this equation:
P′=3(30RR)=3×30=90 W
Final Answer
Thus, the power dissipated when the resistors are connected in parallel across the same source of emf is:
90 W
---
When three equal resistors (let's denote each resistor as R) are connected in series, the total resistance (R_total) is the sum of the individual resistances:
Rtotal=R+R+R=3R
The power (P) dissipated in a resistor can be calculated using the formula:
P=V2Rtotal
Given that the power dissipated in the series configuration is 10 W, we can write:
10=V23R
From the equation above, we can rearrange it to find V2:
V2=10×3R=30R
Now, when the same resistors are connected in parallel, the equivalent resistance (R_eq) is given by:
1Req=1R+1R+1R=3R
Thus, the equivalent resistance is:
Req=R3
Using the same power formula for the parallel configuration, we have:
P′=V2Req
Substituting Req:
P′=V2R3=3V2R
Now we can substitute V2 from Step 3 into this equation:
P′=3(30RR)=3×30=90 W
Thus, the power dissipated when the resistors are connected in parallel across the same source of emf is:
90 W
Topper's Solved these Questions
Similar Questions
(a) Two heater coils made of the same material are connected in paralled across the mains. The length of diameter of one the coil is triple that of other. Which of these will produce more heat?
(b) Three equal resistors connected in series across a source of emf together dissipated 10Wa of power. What would be the power disspated if the same resistors are connected in parallel across the same source of emf?
Two resistor R1 and R2 may be connect either in series or in parellel across a battery of zero internal resistance. it is required that joule heating for the parallel combination be four times than for series combination. if R1=100Ω find R2
(d) The three resistance A,BandC have values 3R,6R and R respectively. Now some potential difference is applied across the network . Find the ratio of thermal powers dissipated between X and Y . find ratio of power consumed by A,B,andC.
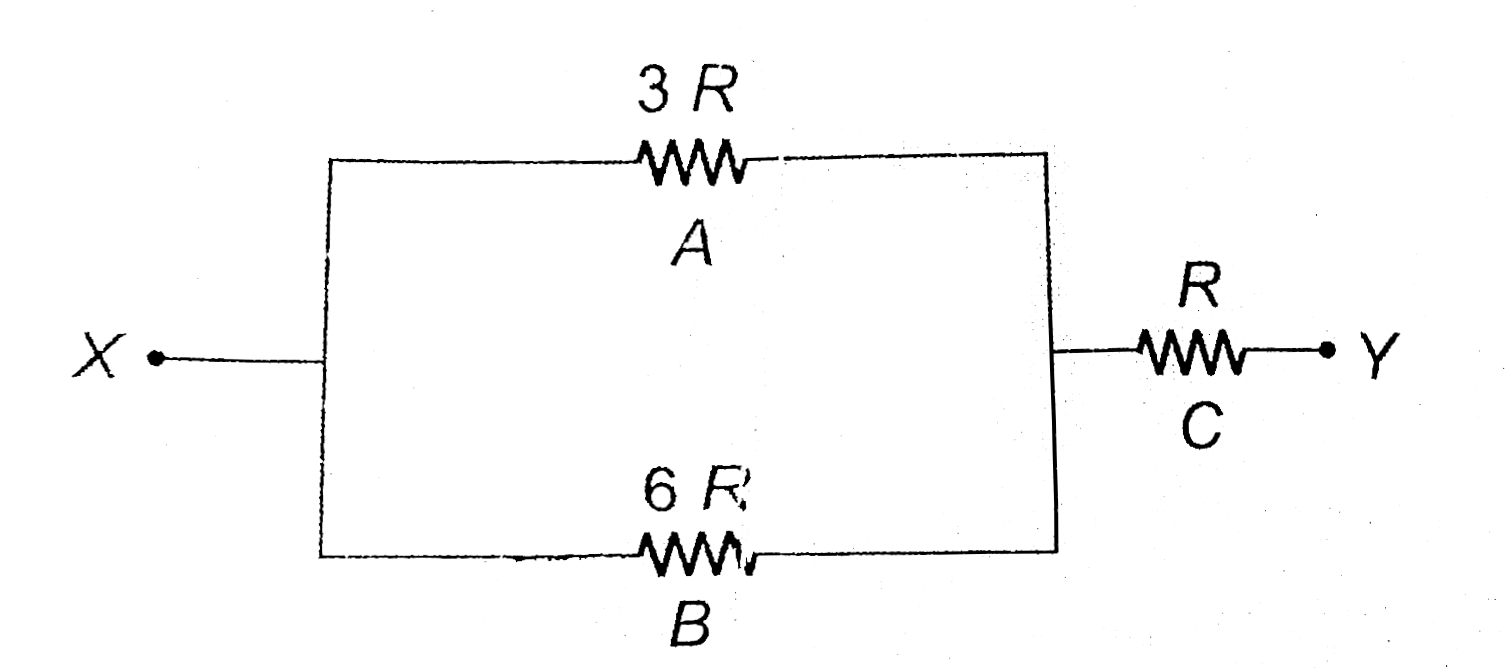
View Solution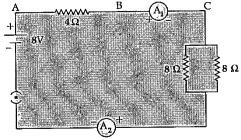
Power dissipated in 4Ω resistor is :
View Solution
Knowledge Check
Three equal resistors connected in series across a source of e.m.f. together dissipate 10 W of power. What should be the power dissipated if the same resistors are connected in parallel across the same source of e.m.f.
A9 WB90 WC10 WD100 WThree equal resistors connected in series across a source of emf together dissipate 10W of power. What would be the power dissipated if te same resistors are connected in parallel across the same source of emf?
A25 WB80 WC45WD90 WThe power dissipated 6Ω resistor is
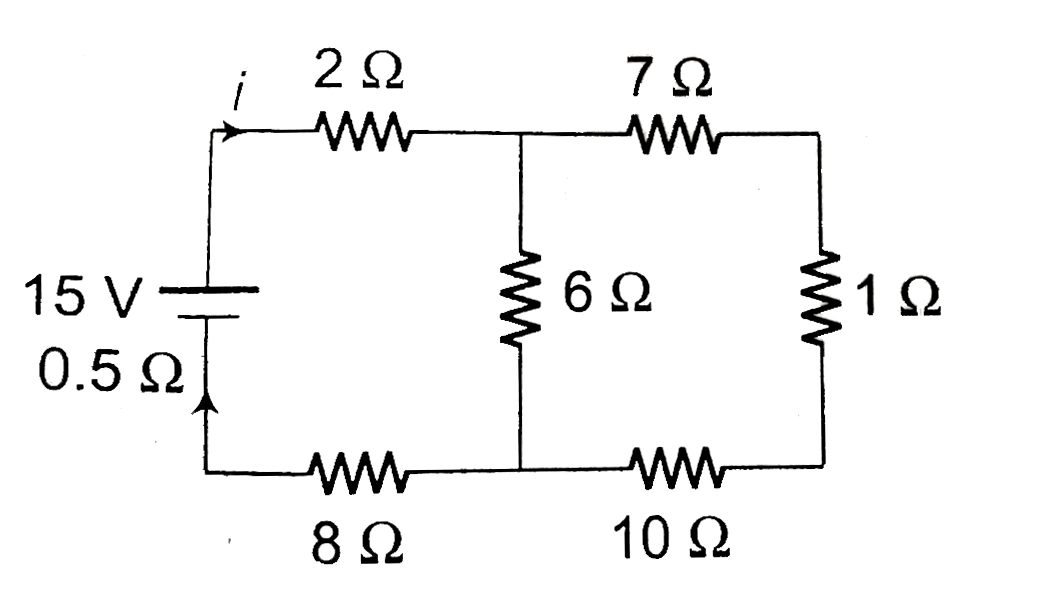 A278WB916WC616WD316W
A278WB916WC616WD316W
Three equal resistors connected in series across a source emf together dissipate 4 watt.If the same resistors are connected in parallel across the same emf the power dissipate will be
View SolutionThree equal resistances connected is series across a source of e.m.f consume 20 watt. If the same resistor are connected in parallel across the same source of e.m.f., what would be the power dissipated ?
View SolutionThree identical resistors are connected in series . When a certain potential difference is applied across the combination , the total power would be dissipated is 27W. How many times the power would be dissipated if the three resistors were connected in parallel across the same potential difference ?
View SolutionThree equal resistor connected in series across a source of enf together dissipate 10Wa. If the same resistors aer connected in parallel across the same emf, then the power dissipated will be
View SolutionFive equal resistors when connected in series dissipated 5 W power. If they are connected in paralle, the power dissipated will be
View Solution

