Consider the situation as shown in the diagram.
The coefficient of friction between the block is 0.5. The acceleration of the lower block is
1m/s2
1.5m/s2
2m/s2
2.5m/s2
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the blocks and calculate the acceleration of the lower block (5 kg) based on the given conditions.
Step 1: Identify the Forces
We have two blocks:
- Block 1 (2 kg) is being pulled by a force of 7 N.
- Block 2 (5 kg) is on the ground and experiences friction from Block 1.
The coefficient of friction (μ) between the blocks is 0.5.
Step 2: Calculate the Normal Force
The normal force (N) acting on Block 1 (2 kg) due to gravity is:
N=m1⋅g=2kg⋅10m/s2=20N
Step 3: Calculate the Limiting Friction
The limiting friction (f) between the two blocks can be calculated using the formula:
fmax=μ⋅N
Substituting the values:
fmax=0.5⋅20N=10N
Step 4: Compare the Applied Force with Limiting Friction
The applied force on Block 1 is 7 N, which is less than the maximum limiting friction of 10 N. Therefore, the frictional force will not be overcome, and both blocks will move together without slipping.
Step 5: Calculate the Acceleration of the System
Since there is no relative motion between the blocks, we can treat them as a single system. The total mass of the system is:
mtotal=m1+m2=2kg+5kg=7kg
Using Newton's second law, the acceleration (a) of the system can be calculated as:
F=mtotal⋅a
Rearranging gives:
a=Fmtotal=7N7kg=1m/s2
Step 6: Conclusion
The acceleration of the lower block (5 kg) is:
a=1m/s2
We have two blocks:
- Block 1 (2 kg) is being pulled by a force of 7 N.
- Block 2 (5 kg) is on the ground and experiences friction from Block 1.
The normal force (N) acting on Block 1 (2 kg) due to gravity is:
N=m1⋅g=2kg⋅10m/s2=20N
The limiting friction (f) between the two blocks can be calculated using the formula:
fmax=μ⋅N
Substituting the values:
fmax=0.5⋅20N=10N
The applied force on Block 1 is 7 N, which is less than the maximum limiting friction of 10 N. Therefore, the frictional force will not be overcome, and both blocks will move together without slipping.
Since there is no relative motion between the blocks, we can treat them as a single system. The total mass of the system is:
mtotal=m1+m2=2kg+5kg=7kg
F=mtotal⋅a
Rearranging gives:
a=Fmtotal=7N7kg=1m/s2
The acceleration of the lower block (5 kg) is:
a=1m/s2
Topper's Solved these Questions
Similar Questions
Consider the situation as shown in the figgure. The coefficent of friction between the blocks is μ. Find the acceleration of each block.

View SolutionConsider the situation shown in the figure . The coefficient of friction between the blocks is μ. Find the minimum and the maximum force F that can be applied so that two blocks move together.

View Solution
Knowledge Check
The block of mass m is in contact with a moving cart as shown in the figure.The coefficient of friction between the block and the cart is . The acceleration a of the cart that will prevent the block from falling is
 Aα≥gμBα<gμCα>mgμDα>gμm
Aα≥gμBα<gμCα>mgμDα>gμmChoose the most appropriate option.
A block of mass mis in contact with the cart C as shown in the figure.
The coefficient of static friction between the block and the cart is u. The acceleration a of the cart that will prevent the block from falling satisfies.
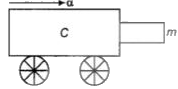 Aα>mgμBα>g2μCα≥gμDα<gμ
Aα>mgμBα>g2μCα≥gμDα<gμConsider the arrangement shown in the figure. The coefficient of friction between the two blocks is 0.5 and between the 4 kg block and the horizontal surface is 0.4. If a horizontal force of 12 N is applied on the 4 kg block, the acceleration of the 2 kg block would be
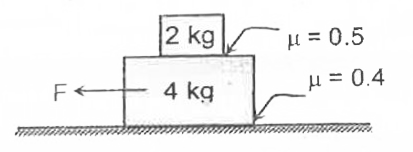 A2.5m/s2B2m/s2C5m/s2Dzero
A2.5m/s2B2m/s2C5m/s2Dzero
The coefficient of friction between the block and the inclined plane is μ.
View SolutionThe coefficient of friction between the blocks is 0.5. Find the acceleration of each block if Fis(a)21N,(b)35 Nand(c)40 N.

View SolutionA block of mass m is in contact with the cart C as shown in the figure

The coefficient of static friction between the block and the cart is μ. The acceleration α of the cart that will prevent the block from falling satisfies.
View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
View SolutionConsider the shown arrangement. The coefficient of friction between the two blocks is 0.5 . There is no friction between the 4 kg block and of 12 N is applied on the 2 kg block as shown in the figure, the acceleration of the 4 kg block would be

View Solution