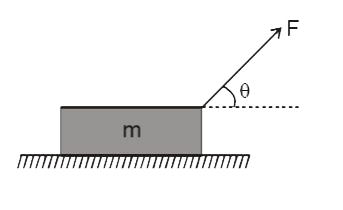
A block of mass $m$ rests on a horizontal floor for which coefficient of friction is $μ$ . Find the magnitude and the direction of force that should be applied to just move the block so that the applied force is minimum.

Video Solution

Text Solution

Verified by Experts

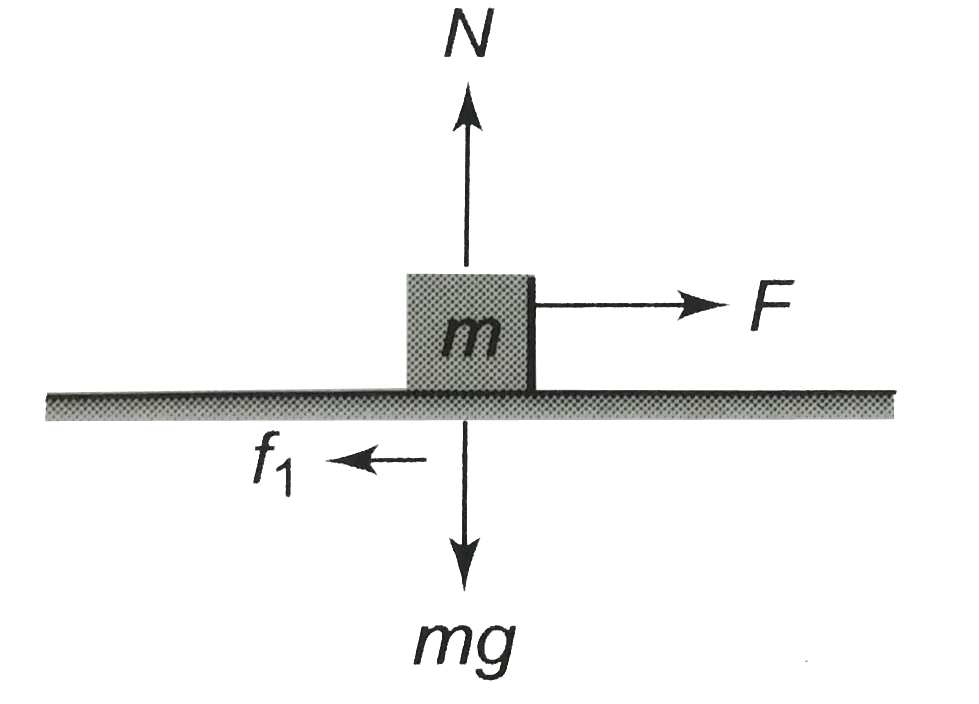
(a) If force is applied horizontally
${(f_{1})}_{max} = μ N = μ m g$ (i)
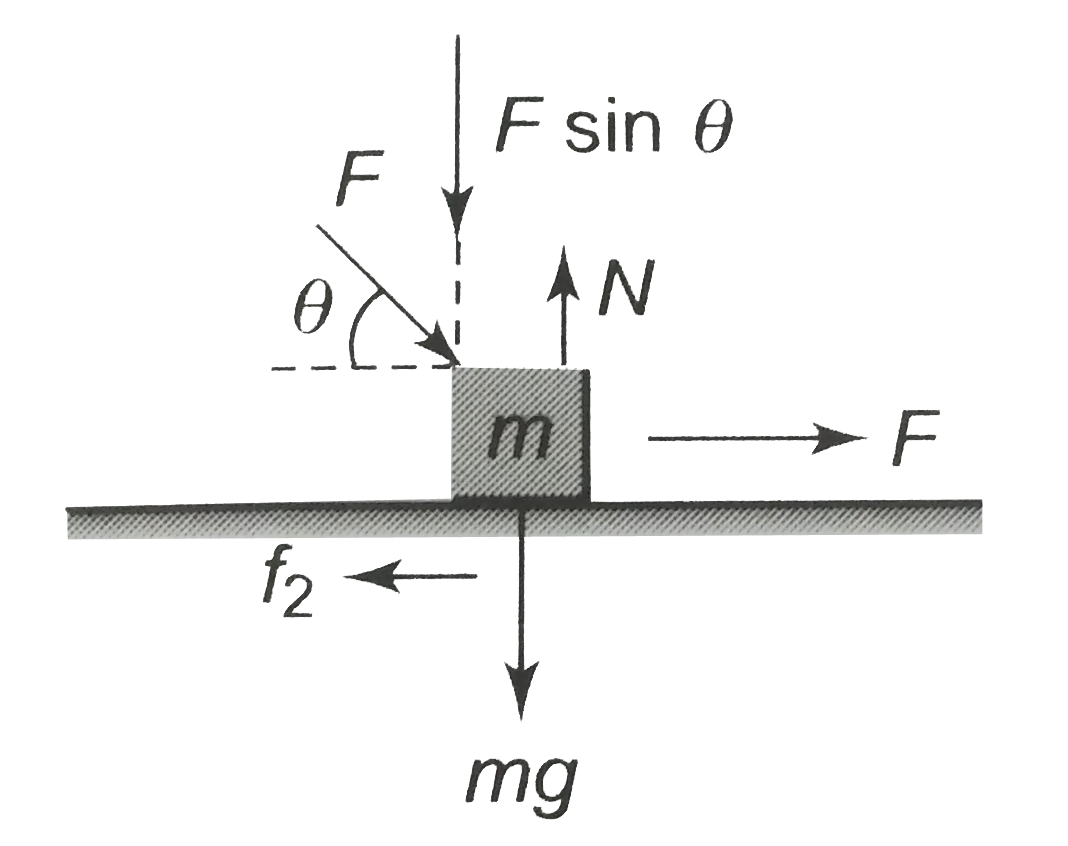
(b) If the block is pushed by applying a force at an angle with horizontal
$N = m g + F sin θ$
${(f_{2})}_{max} = μ N = μ (m g + F sin θ)$ (ii)
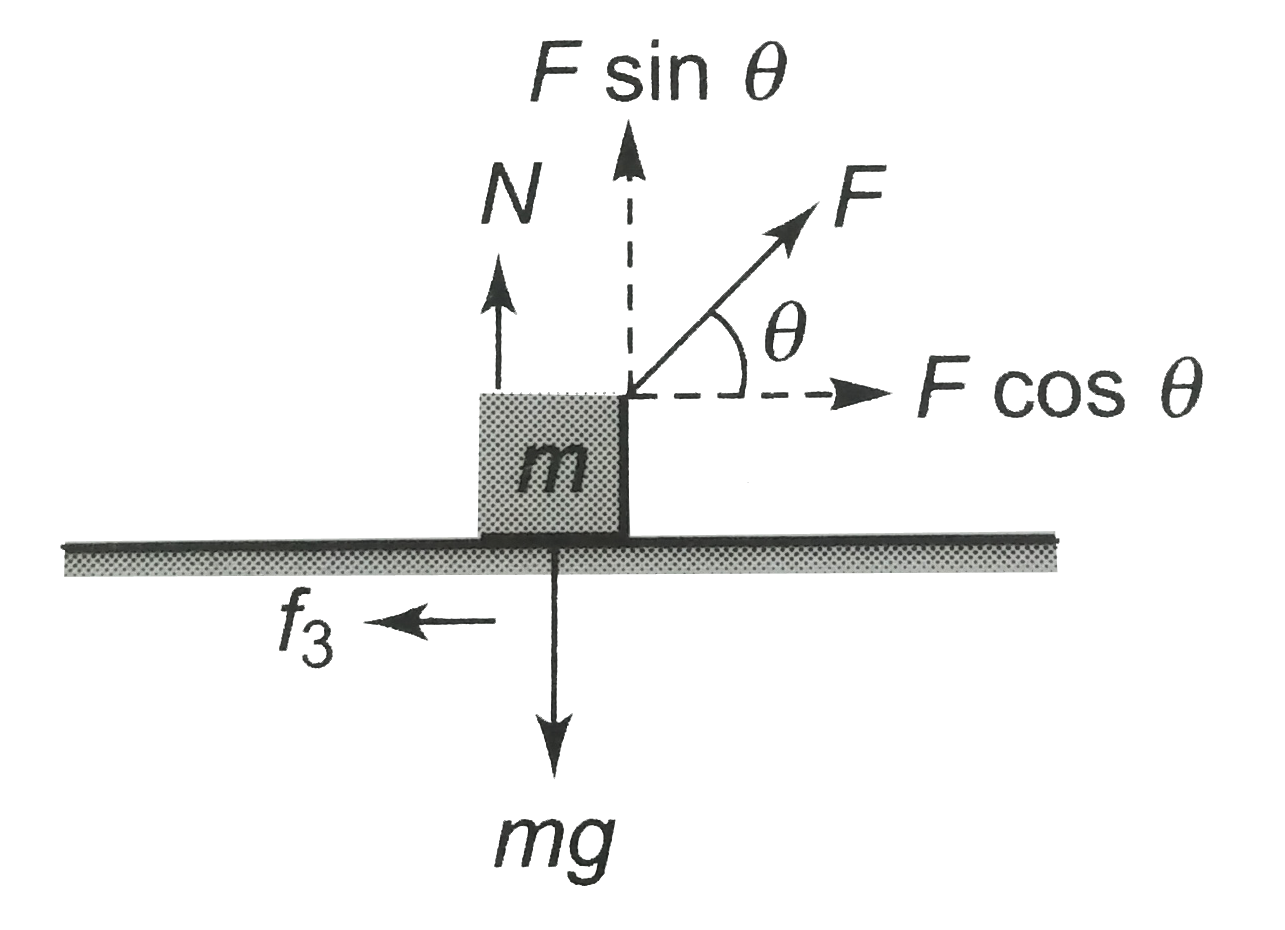
(c ) If the block is pulled by applying a force at an angle with horizontal
$N + F sin θ = m g$
$\Rightarrow N = m g - F sin θ$
${(f_{3})}_{max} = μ N = μ N = μ (m g - F sin θ)$ (iii)
${(f_{3})}_{max} < {(f_{1})}_{max} < {(f_{2})}_{max}$
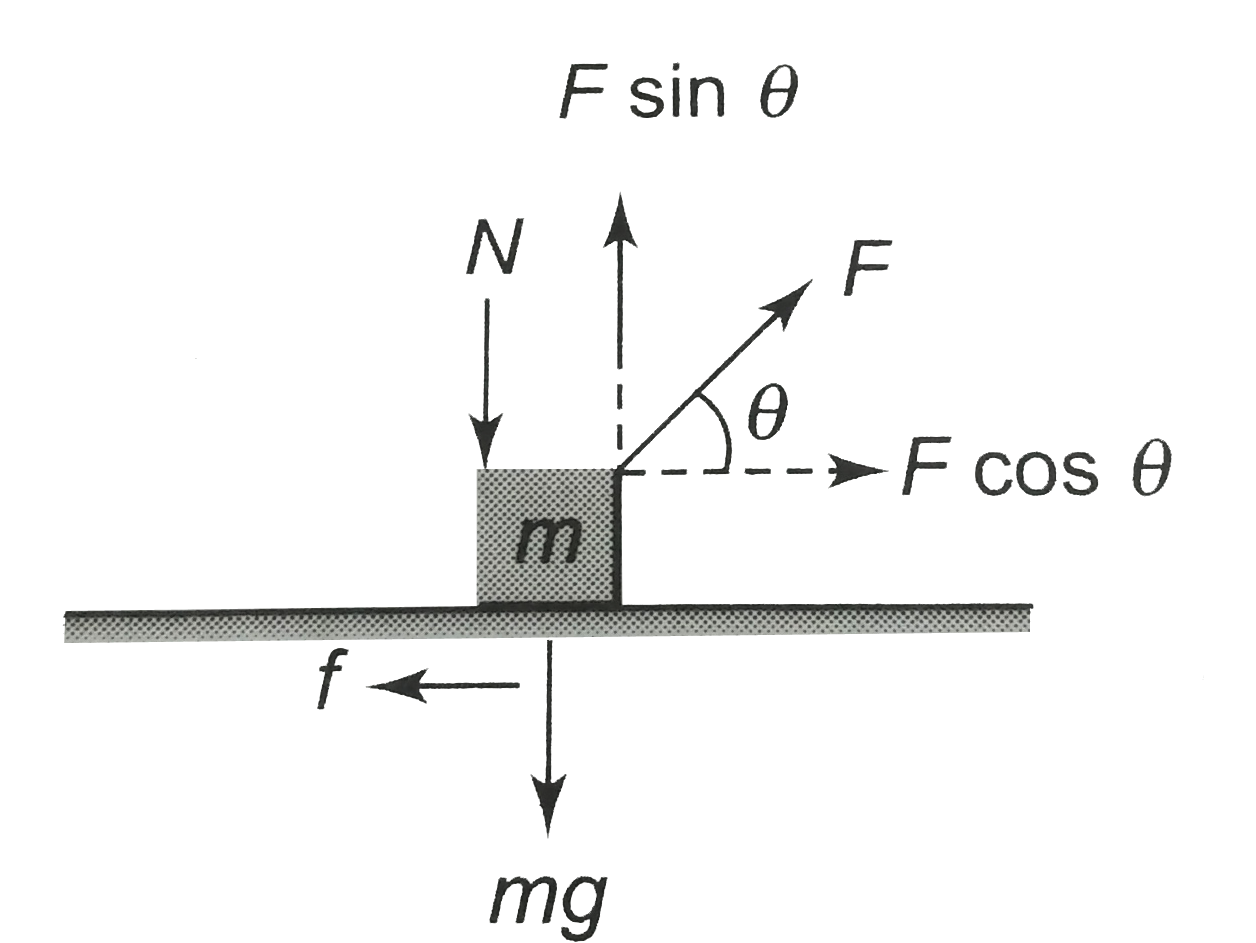
To move a block , the friction is minimum , when the block is pulled by applying a force at an angle with horizontal
$N + F sin θ = m g \Rightarrow N = m g - F sin θ$
The block is about to move if
$F cos θ = f_{max} = μ N = μ (m g - F sin θ)$
$F = \frac{μ m g}{cos θ + μ sin θ}$
Let the denominator $k = cos θ + μ sin θ$
For $F$ to be minimum , $k$ must be maximum.
$\Rightarrow \frac{d k}{d θ} = - sin θ + μ cos θ = 0$
$tan θ = μ \Rightarrow θ = {tan}^{- 1} (μ)$
$sin θ = \frac{μ}{\sqrt{1 + μ^{2}}}$
$cos θ = \frac{μ}{\sqrt{1 + μ^{2}}}$
$F_{min} = \frac{μ m g}{\frac{1}{\sqrt{1 + μ^{2}}} + \frac{μ \times μ}{\sqrt{1 + μ^{2}}}} = \frac{μ m g}{\sqrt{1 + μ^{2}}}$

Updated on:21/07/2023

A block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is $0.5 .$ then the minimum force required to move the block is :-

A10 N
B $\frac{100}{11} N$
C $\frac{100}{8} N$
D20 N
A block of mass $m = 5 k g$ is resting on a rough horizontal surface for which the coefficient of friction is $0.2$ . When a force $F = 40 N$ is applied, the acceleration of the block will be $(g = 10 m / s^{2})$ .

A $5.73 m / {sec}^{2}$
B $8.0 m / {sec}^{2}$
C $3.17 m / {sec}^{2}$
D $10.0 m / {sec}^{2}$
A blocky of mass m rests on a horizotal floor with which it has a coefficient of static friction $μ .$ It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has be applies.
A $μ m g$
B $\frac{\sqrt{1 + μ^{2}}}{μ} m g$
C $μ \sqrt{1 + μ^{2}} m g$
D $\frac{μ m g}{\sqrt{1 + μ^{2}}}$