Consider a bob whose upper and is fixed with length of 2 m is given with a horizontal push through angular displacement of 60∘ . What is the angular velocity of the bob ? If it is of 2kg . [Take ,g=10ms−2]
√10rads−1
√20rads−1
√8rads−1
None of these
The correct Answer is:A
Given , mass ,= 2kg
angular displacement ,θ=60∘
length,l=2mandg=10ms−2

From FBD, we have Tcosθ=mg (i)
Tsinθ=mgω2 (ii)
From Eqs.(i) and (ii) ,We get
ω=√gtanθr
Also " " r=lsinθ
∴ ω=√gsinθcosθ×lsinθω=√glcosθ=√102×cos60∘=√101⇒ ω=√10rads−1
Topper's Solved these Questions
- CIRCULAR MOTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:CIRCULAR MOTIONExercise:EXERCISE 1
Explore 54 Videos
- CIRCULAR MOTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:CIRCULAR MOTIONExercise:EXERCISE 2 (Miscellaneous Problems)
Explore 25 Videos
- ATOMS, MOLECULES AND NUCLEI Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ATOMS, MOLECULES AND NUCLEI Exercise:MHT CET Corner
Explore 30 Videos
- COMMUNICATION SYSTEMBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:COMMUNICATION SYSTEMExercise:MHC CET Corner
Explore 6 Videos
Similar Questions
The bob of pendulum is project with horizontal velocity of √3gf I is the length of string. Find the angular displacement of string before it becomes slack.

View SolutionThe given figure shows the variation of the kinetic energy of a simple pendulum with its angular displacement (θ) from the vertical. Mass of the pendulum bob is m = 0.2 kg. Find the time period of the pendulum. Take g=10ms−2.
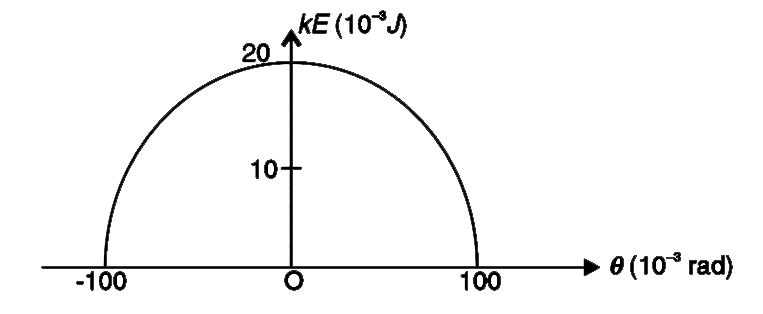
View Solution
Knowledge Check
If a simple pendulum of length l has maximum angular displacement θ, then the maximum velocity of the bob is
A√LgB2√glsin(θ2)C√2glsinθD√2glA simple pendulum having a bob of mass 100 g is oscillating with a maximum angular displacement of 3∘. The maximum restoring force acting on the bob is (take g=10ms−2)
Aπ60NB50π3NC3ND3000 NA rod AB of length 1m is placed at the edge for a smooth table as shown in figure. It is hit horizontally at point B. If the displacement of centre of mass m in 1s is 5√2m. The angular velocity of the rod is (g=10m/s2)
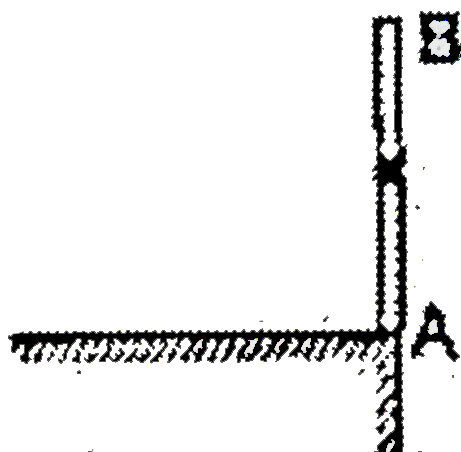 A30rad/sB20rad/sC10rad/sD5rad/s
A30rad/sB20rad/sC10rad/sD5rad/s
The angular displacement of particle (in radian) is given by θ=t2+t. Calculate angular velocity at t=2 second.
View SolutionA simple pendulum with a bob of mass 'm' swings with angular amplitude of 60∘. When its angular displacement is 30∘, the tension in the strings would be
View SolutionA simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
View SolutionA simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View SolutionThe bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View Solution