Select the correct alternatives for an ideal gas :
The change in internal energy un a constant pressure process from temperature is equal to is the molar specific heat at constant volume and n the number of moles of the gas.
The change in internal energy of the gas and the work done by the gas are equal in magnitude in an adiabatic process.
The internal energy dose not change in an isothermal process.
No heat is added or removed in an asiabatic process.
The correct Answer is:A, B, C, D
(a)
ltBRgt
(b)
But for adiabatic process, hence
(c)
(d) (in adiabatic change)
Topper's Solved these Questions
Similar Questions
Knowledge Check
Select the correct alternative(s)
AWork done by kinetic friction on a body always results in a loss of its kinetic energy.BWork done on a body, in the motion of that body over a close loop is zero for every force in nature.CTotal mechanical energy of a system is always conserved no matter what type of internal and ecternal forces on the body are present.DWhen total work done by a conservative force on the system is positive then the potential energy associated with this force decreases.Select the correct alternative(s).
AWork done by kinetic friction on a body always results in a loss of its kinetic energy.BWork done on a body, in the motion of that body over a close loop is zero for every force in nature.CTotal mechanical energy of a system is always conserved no matter what type of internal and ecternal forces on the body are present.DWhen total work done by a conservative force on the system is positive then the potential energy associated with this force decreases.Select the correct alternative (s)
AWork done by kinetic friction on a body always results in a loss of its kinetic energy.BWork done on a body, in the motion of that body over a close loop is zero for every force in nature.CTotal mechanical energy of a system is always conserved no matter what type of internal and ecternal forces on the body are present.DWhen total work done by a conservative force on the system is positive then the potential energy associated with this force decreases.
P - V diagram of an ideal gas is shown. The gas undergoes from initial state A to final state B such that initial and final volumes are same. Select the correct alternative for given process AB.
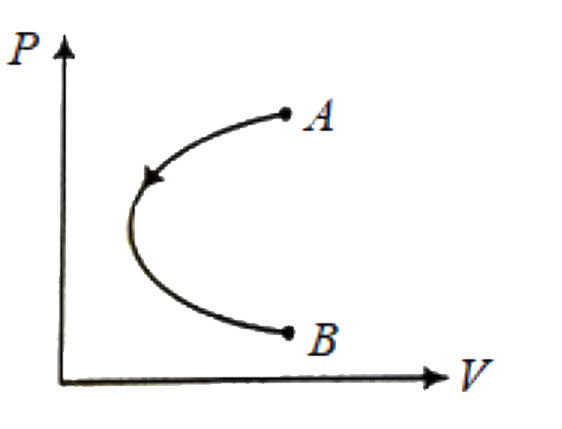
View SolutionSelect the correct option for an ideal gas undergoing a process as shown in diagram.
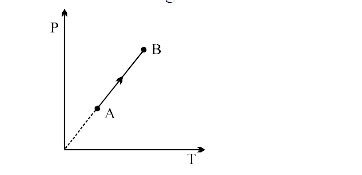
View SolutionSelect the correct alternative from the given options .
The gas assimilated by plants for the synthesis of proteins is _________.
View SolutionSelect the correct alternative for the endothermic change.
View SolutionSelect the correct alternate about entropy
View Solution

