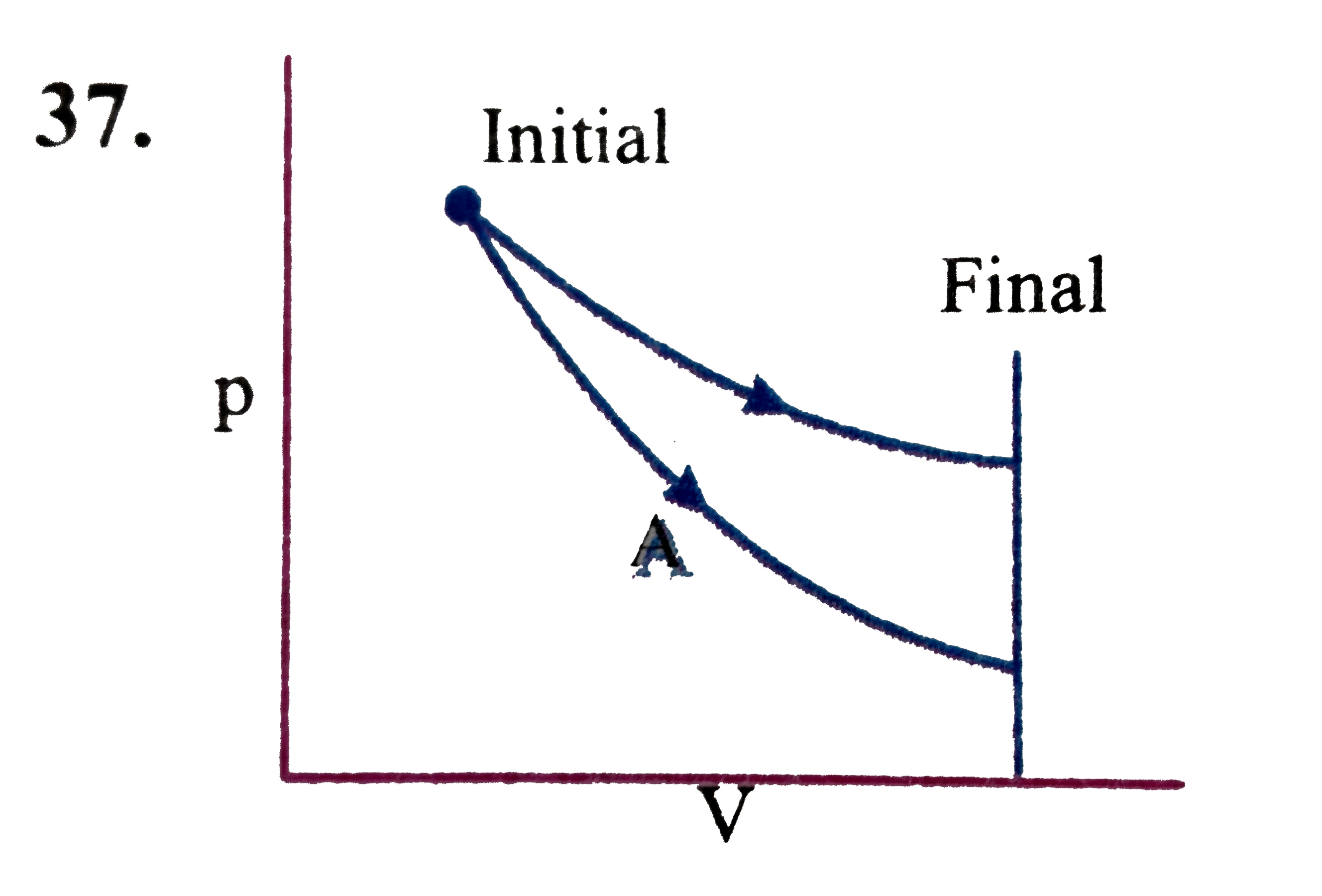
Two gases have the same initial pressure, volume and temperature. They expand to the same final volume, one adiabatically and the other isothermally
the final temperature is greater for the isothermal process
the final pressure is greater for the isothermal process
the work done by the gas in greater for the isothermal process
all the above options are incorrect
The correct Answer is:A, B, C
Topper's Solved these Questions
Similar Questions
Two gases have the same initial pressure P, volume V and temperature T. They both expand to the same volume from V to 2V, one adiabatically and the other isothermally. Plot P-V diagram for the given situation and hence explain. In which case is the final temperature greater?
View SolutionConsider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas is container B is compressed to half of its original vlue adiabatically. The ratio of final pressure of gas of B to that of gas in A is
View Solution
Knowledge Check
Statement-1: Two gases at same pressure, volume & temperature are compressed to same volume. The first isothermally and second adiabatically, greater work is done on the gas for an adiabatic process.
Statement-2: Final temperature for gas going under isothermal process is more than gas going under adiabatic process.AStatement-1 is true, statement-2 is true, statement-2 is a correct explanation for statement-1BStatement-1 is true, statement-2 is true, statement-2 is NOT a correct explanation for statement-1CStatement-1 is true, statement-2 is falseDStatement-1 is false, statement-2 is trueConsider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is
A2γ−1B(12)γ−1C(11−γ)2D(1γ−1)2Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is
A2γ−1B(12)γ−1C(11−γ)2D(1γ−1)2
Two different ideal diatomic gases A and B are initially in the same state. A and B are then expanded to same final volume through adiabatic and isothermal process respectively. If PA,PB and TA,TB represents the final pressure and temperature of A and B respectively then.
View SolutionConsider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermal while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is
View SolutionTwo gases A and B having the same pressure P, volume V and temperature T are mixed. If mixture has volume and temperature as V and T respectively, then the pressure of the mixture will be
View SolutionTwo identical samples of gases are allowed to expand to the same final volume (i) isothermally (ii) adiabatically. Work done is
View SolutionAt the same conditions of pressure, volume and temperature, work done is maximum for which gas if all gases have equal masses?
View Solution