If TB and Ts are the temperatures of the body and the surroundings and TB−Ts is of very high value, then the rate of cooling in natural convection is proportional to .
T4B
T4S
(TB−TS)54
(T54B−T54S)
The correct Answer is:A
To solve the problem, we need to determine how the rate of cooling in natural convection relates to the temperature difference between a body and its surroundings when that temperature difference is very high.
1. Understanding the Variables:
- Let TB be the temperature of the body.
- Let Ts be the temperature of the surroundings.
- The difference TB−Ts is given to be very high.
2. Applying Newton's Law of Cooling:
- In natural convection, the rate of cooling is generally described by Newton's Law of Cooling, which states that the rate of heat loss of a body is proportional to the temperature difference between the body and its surroundings.
- Mathematically, this can be expressed as:
dQdt∝(TB−Ts)
- Here, dQdt is the rate of heat loss.
3. Considering High Temperature Difference:
- Since TB−Ts is very high, we can say that the body is significantly hotter than the surroundings.
- This implies that the temperature of the surroundings Ts can be considered negligible compared to TB.
4. Simplifying the Expression:
- If we denote ΔT=TB−Ts, then for very high values of ΔT:
dQdt∝ΔT
- This means that the rate of cooling is directly proportional to the temperature difference ΔT.
5. Conclusion:
- Therefore, the rate of cooling in natural convection is proportional to the temperature difference TB−Ts when this difference is very high.
Final Answer:
The rate of cooling in natural convection is proportional to TB−Ts.
---
- Let TB be the temperature of the body.
- Let Ts be the temperature of the surroundings.
- The difference TB−Ts is given to be very high.
- In natural convection, the rate of cooling is generally described by Newton's Law of Cooling, which states that the rate of heat loss of a body is proportional to the temperature difference between the body and its surroundings.
- Mathematically, this can be expressed as:
dQdt∝(TB−Ts)
- Here, dQdt is the rate of heat loss.
- Since TB−Ts is very high, we can say that the body is significantly hotter than the surroundings.
- This implies that the temperature of the surroundings Ts can be considered negligible compared to TB.
- If we denote ΔT=TB−Ts, then for very high values of ΔT:
dQdt∝ΔT
- This means that the rate of cooling is directly proportional to the temperature difference ΔT.
- Therefore, the rate of cooling in natural convection is proportional to the temperature difference TB−Ts when this difference is very high.
The rate of cooling in natural convection is proportional to TB−Ts.
Topper's Solved these Questions
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL -1 (C.W)
Explore 1 Video
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL (C.W)
Explore 13 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL-II(C.W)
Explore 27 Videos
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Exercise
Explore 187 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:STATEMENT TYPE QUESTION
Explore 23 Videos
Similar Questions
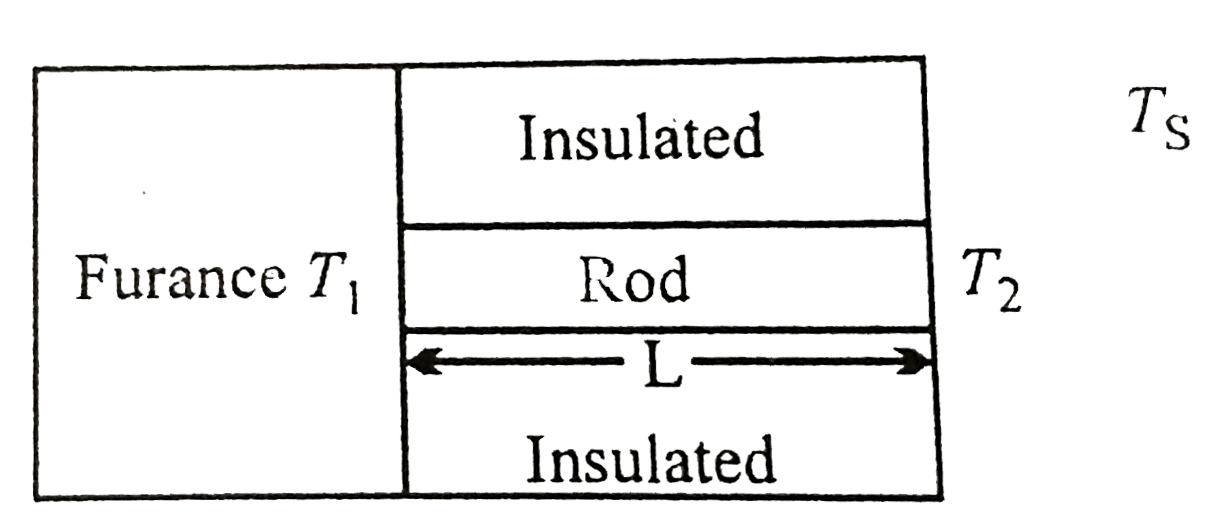
One end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
View SolutionA very thin metallic shell of radius r is heated to temperature T and then allowed to cool. The rate of cooling of shell is proportional to
View Solution
Knowledge Check
According to ‘Newton’s Law of cooling’, the rate of cooling of a body is proportional to the
ATemperature of the bodyBTemperature of the surroundingCFourth power of the temperature of the bodyDDifference of the temperature of the body and the surroundingsIf the temperature of the body θ and time of cooling 't' and room temperature of the surrounding θ0. The cooling curve is
A B
B C
C D
D
A body at higher temperature T K radiates heat at a rate which is proportional to
ATBT2CT−4DT4
A metal piece is heated up to T K. The temperature of the surrounding is t K. The heat lost to the surrounding due to radiation is proportional to
View SolutionA metal piece is heated up to T K. The temperature of the surrounding is t K. The heat lost to the surrounding due to radiation is proportional to
View SolutionA metal piece is heated up to T K. The temperature of the surrounding is t K. The heat lost to the surrounding due to radiation is proportional to
View SolutionThe rate at which a black body emits radiation at a temperature T is proportional to
View SolutionThe rate at which a black body emits radiation at a temperature T is proportional to
View Solution

