A fisherman hooks an old log of wood of weight 12 N and volume 1000 cm3. He pulls the log half way out of water. The tension in the string at this instant is
12 N
8 N
10 N
7 N
Tension (T)= weight (mg)− force of buoyancy (FB)⇒T=Mg−(V2)dwg
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Illustration
Explore 62 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EVALUATE YOURSELF - 1
Explore 2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Level 1 (H.W)
Explore 55 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
A string is wrapped around a log of wood and it is pulled with a force F as shown in
(b) How does the value of tension T in the string change with θ when will the tension T be greater than applied force?
View SolutionAn iron casting containing a number of cavities weight 6000N in air and 4000N in water. What is the volume of the cavities in the casting? Density of iron is 7.87g/cm3. Take g=9.8m/s2 and density of water =103kg/m3.
View Solution
Knowledge Check
A thin metal ring of internal radius 8 cm and external radius 9 cm is supported horizontally from the pan of a balance so that it comes in contact with water in a glass vessel. If is found that an extrea weight of 7.48g is required to pull the ring out of water. The surface tension of water is (g=10m/s2)
A80×10−3N/mB25×10−3N/mC45×10−3N/mD70×10−3N/mIn two identical communicating vessel we poured water (see picture). In one of them we put an ice ball of volume V=100cm3 which gets exactly half immersed in the water. The density of water ρw=1000kg/m3 the density of ice ρi=900kg/m3
 Which of the following actions will raise the water level.AHeating the systemBPutting a coin on top of ice ball.CPutting a coin in right vesselDAccelerating the system upwards.
Which of the following actions will raise the water level.AHeating the systemBPutting a coin on top of ice ball.CPutting a coin in right vesselDAccelerating the system upwards.In two identical communicating vessel we poured water (see picture). In one of them we put an ice ball of volume V=100cm3 which gets exactly half immersed in the water. The density of water ρw=1000kg/m3 the density of ice ρi=900kg/m3
 Select the correct statement (s). Soon after placing the ice ball in left vessel.AThe volume of water flowing to the right vessel is 25cc.BThe volume of water flowing to the right vessel is 50ccCThe ice ball is resting on the bottom of vessel.DThe ice ball is floating on the water surface.
Select the correct statement (s). Soon after placing the ice ball in left vessel.AThe volume of water flowing to the right vessel is 25cc.BThe volume of water flowing to the right vessel is 50ccCThe ice ball is resting on the bottom of vessel.DThe ice ball is floating on the water surface.
A steel wire of length 7 m and cross section 1mm2 I suspended from a rigid support, with a steel weight of volume 103cm3 hanging from its other end. Find the decrease in the length of the wire when the steel weight is completely immersed in water.
Ysteel=2×1011N/m2 density of water =103kg/m3 ]
View SolutionIn two identical communicating vessel we poured water (see picture). In one of them we put an ice ball of volume V=100cm3 which gets exactly half immersed in the water. The density of water ρw=1000kg/m3 the density of ice ρi=900kg/m3
 After a long time, select the correct statement (s)
After a long time, select the correct statement (s)
View SolutionA tank of large base area is filled with water up to a height of 5m. A hole of 2cm2 cross section in the bottom allows the water to drain out in continuous streams. For this situation, mark out the correct statement(s) (take ρwater=1000kg/m3,g=10ms−12)

View SolutionThree identical blocks each of mass m=1kg and volume 3×10−4m3 are suspended by massless strings from a support as shown. Underneath are three identical containers containing the same amount of water that are placed over the scales. In Fig. (a), the block is completely out of the water, in Fig. (b), the block is completely submerged but not touching the beaker and in Fig. (c), the block rests on the bottom of the beaker. The scale in Fig (a) reads 14N.
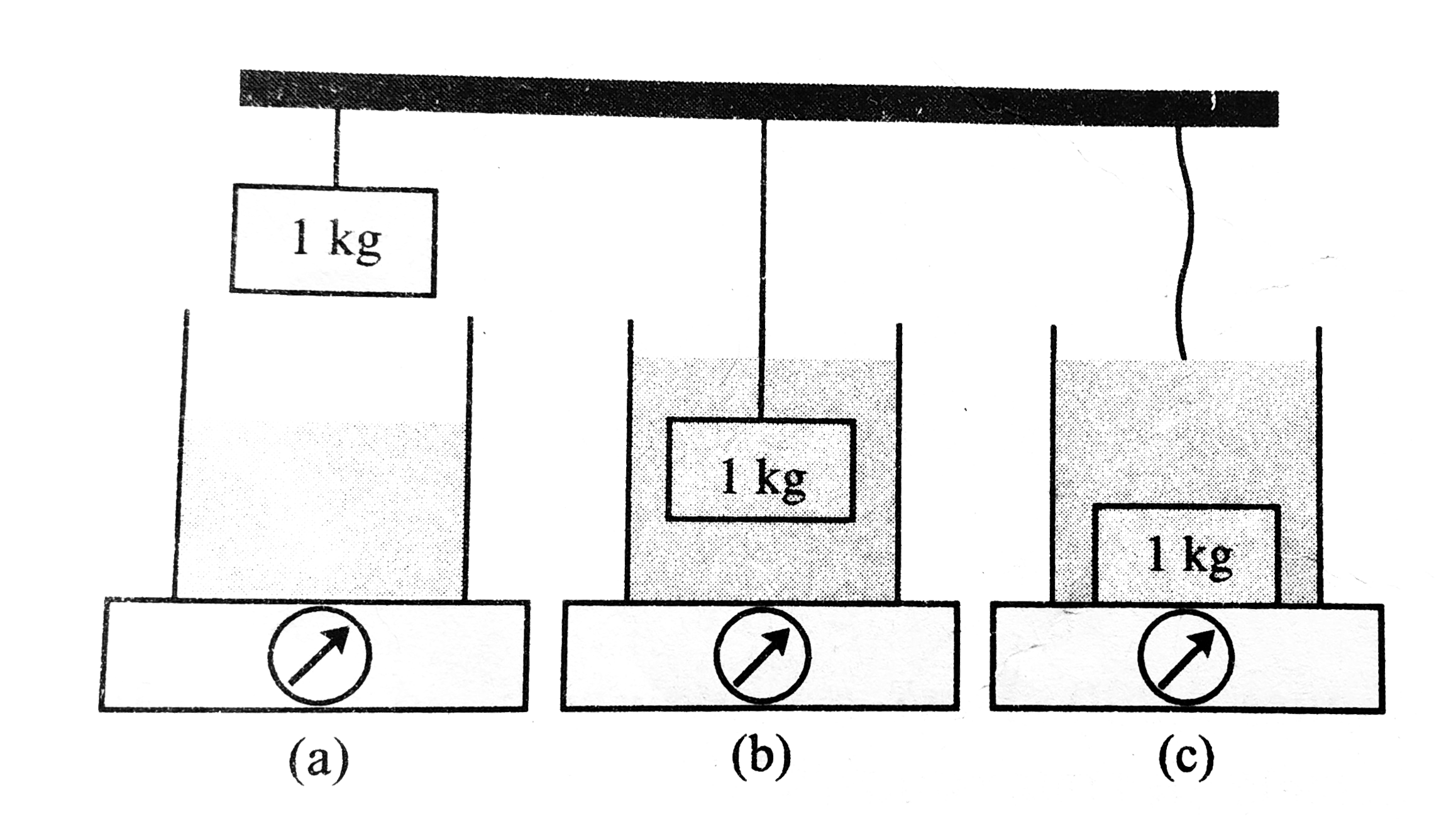
View SolutionA wooden block of volume 1000cm3 is suspended from a spring balance its weight is 12 N in air. It is suspended in water such that half of the block is below the surface of water. The reading of spring balance is
View Solution

