A siphon has a uniform circular base of diameter 8/√πcm with its crest A,1.8m above the water level vessel B is of large cross section (g=10m/s2 and atmospheric pressure P0=105N/m2).
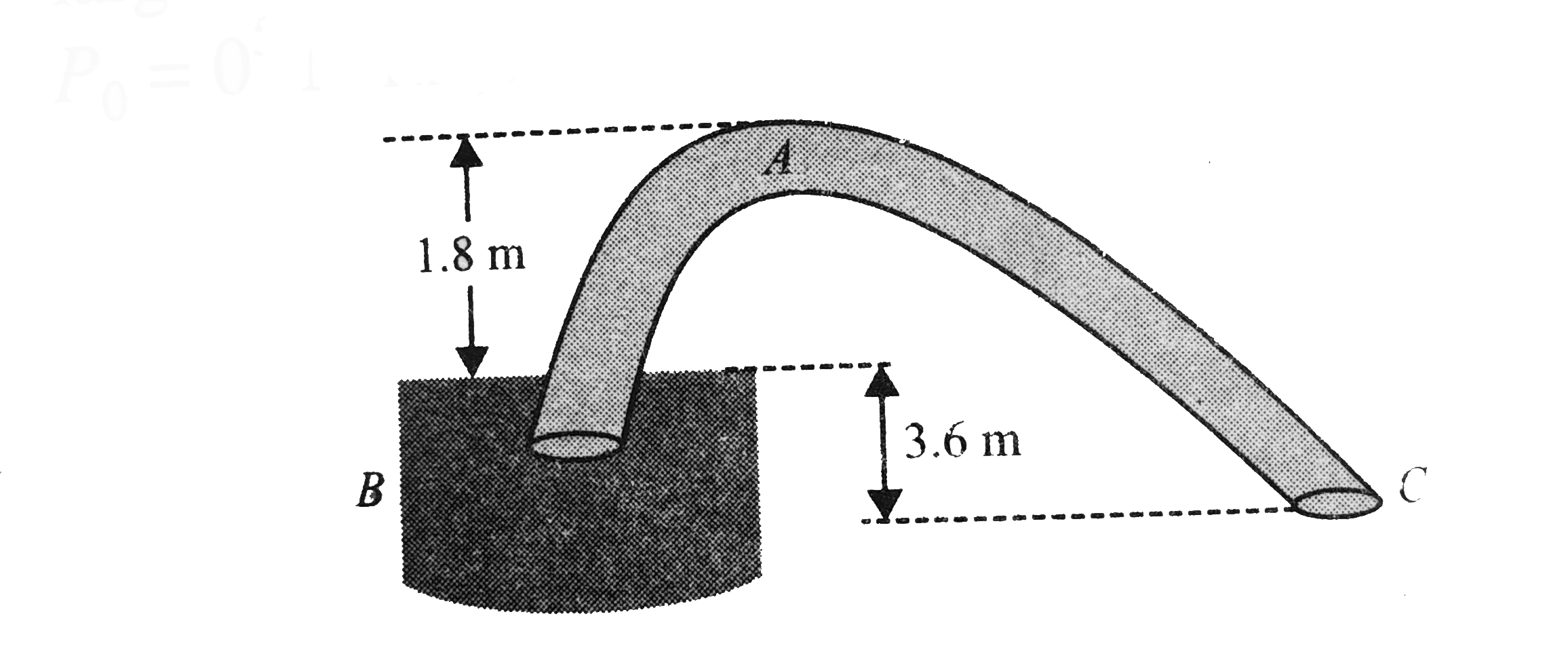
velocity of flow through pipe is 6√2m/s
Discharge rate of flow through pipe is 96√2×10−4m3/s
Velocity of flow through pipe is 6m/s
Pressure of A is 0.46×1−5N/m2
The correct Answer is:A, B, D
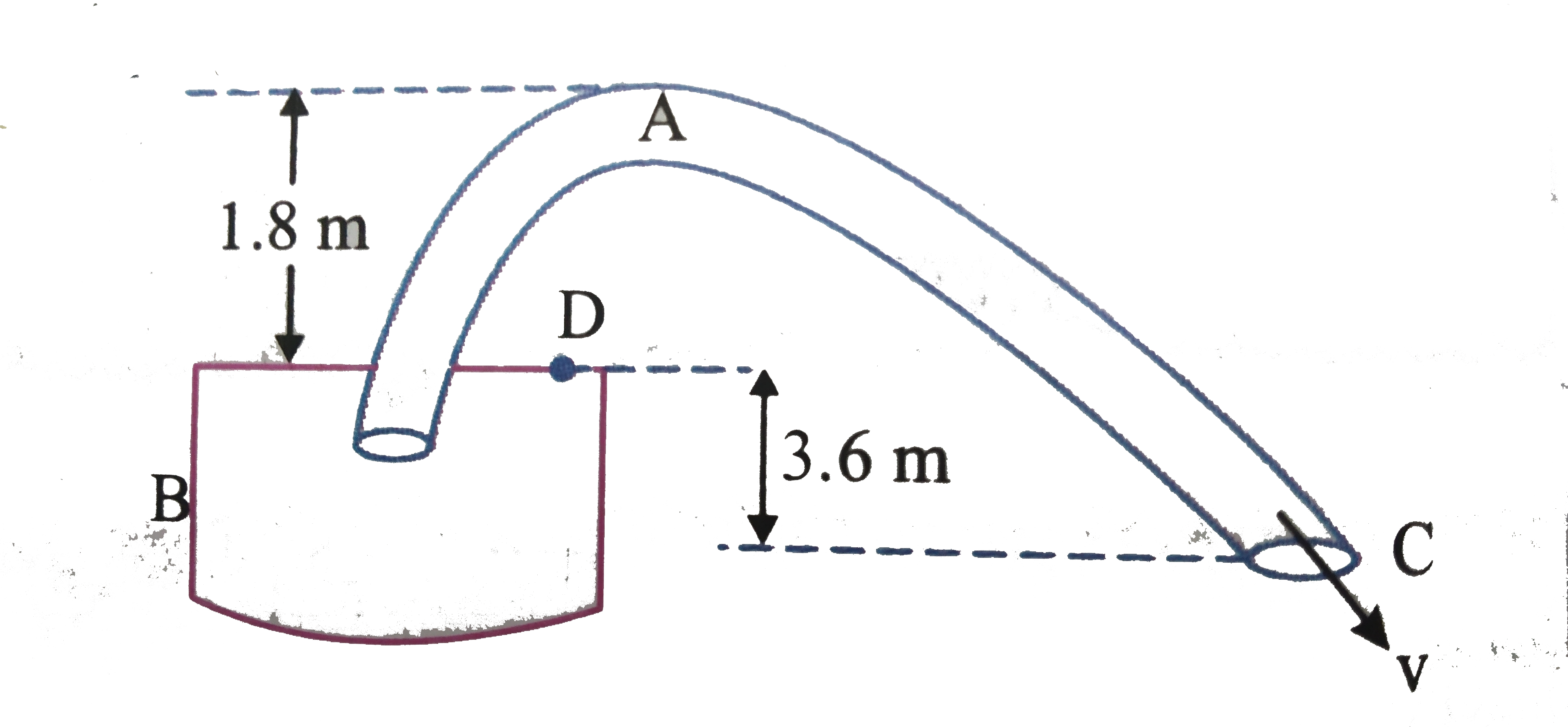
Applying bernoulli's equation at C and D, we have
P0+0+ρg(3.6)=P0+12ρv2+0⇒v=6√2m/s
Volume blown per unit time =av=πr2v=96√2
Similarly at A and C,
PA+12ρv2+ρg(3.6+1.8)=P0+12ρv2+0
PA=0.47×105N/m2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Comprehension Type Questions
Explore 40 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Paragraph Type Questions
Explore 5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Statement Type Questions
Explore 16 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
A rigid cylindrical container having a cross sectional area of 0.2m2 is filled with water up to a height of 5.0m. There is a piston of negligible mass over the water. Piston can slide inside the container without friction. When a weight of 2000kg is placed over the piston, it moves down by 0.25 mm compressing the water.
ρ= Density of water =103kg/m2,Patm= Atmospheric pressure =105N/m2 and g=10m/s2. With this information calculate the speed of sound in water.

View SolutionWhat is the absolute pressure on a swimmer 10m below the surface of a lake? Take atmospheric pressure 1×105N/m2
View Solution
Knowledge Check
A siphon has a uniform circular base of diameter 8/√πcm with its crest A,1.8m above the water level vessel B is of large cross section (g=10m/s2 and atmospheric pressure P0=05N/m2).
 Avelocity of flow through pipe is 6√2m/sBDischarge rate of flow through pipe is 96√2×10−4m3/sCVelocity of flow through pipe is 6m/sDPressure of A is 0.46×10−5N/m2
Avelocity of flow through pipe is 6√2m/sBDischarge rate of flow through pipe is 96√2×10−4m3/sCVelocity of flow through pipe is 6m/sDPressure of A is 0.46×10−5N/m2One bar is equivalent of 105N/m2. The atmosphere pressure is 1.0313×105N/m2. The same in bar is
A1.88 barB1.013 barC2.013 barDnone of theseA glass capillary tube (closed from tap) of inner diameter 0.28mm is lowered vertically into water in a vessel. The pressure in the capillary tube so that water level in the tube is same as that in the vessel is N/m2 is (surface tension of water =0.7N/m and atmospheric pressure =105N/m2.
A103B99×103C100×103D101×103
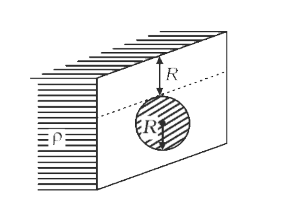
Find the hydrostatic force (in kN) acting on the circular patch of radius R.(R=1m,g=10m/s2 , atmospheric pressure = 10 ^(5 ) Pa )
View SolutionA vessel full of water has a bottom of area 20cm2, top of area 20cm2, height 20 cm and volume half a litre as shown in figure.
(a) find the force exerted by the water on the bottom.

(b) considering the equilibrium of the water, find the resultant force exerted by the sides of the glass vessel on the water. atmospheric pressure =1.0×105N/m2. density of water =1000kg/m3 and g=10m/s2
View SolutionA glass capillary tube of inner diameter 0.28mm is lowered verically into water in a vessel. The pressure to be applied on the water in the capillary tube so that water level in the tube is same as that in the vessel is λ×105N/m2. Then find λ in nearest integer (surface tension of water =0.07N/m and atmospheric pressure =105N/m2) :
View SolutionThe U-tube acts as a water siphon. The bend in the tube is 1m above the water surface. The tube outlet is 7m below the water surface. The water issues from the bottom of the siphon as a free jet at atmospheric pressure. Determine the speed of the free jet and the minimum absolute pressure of the water in the bend. Given atmospheric pressure =1.01×105N/m2,g=9.8m/s2 and density of water =103kg/m3
 .
.
View SolutionA glass capillary tube of inner diameter 0.28 mm is lowered vertically into water in a vessel. The pressure to be applied on the water in the capillary tube so that water level in the tube is same as the vessel in Nm2 is (surface tension of water =0.07Nm atmospheric pressure =105Nm2
View Solution

