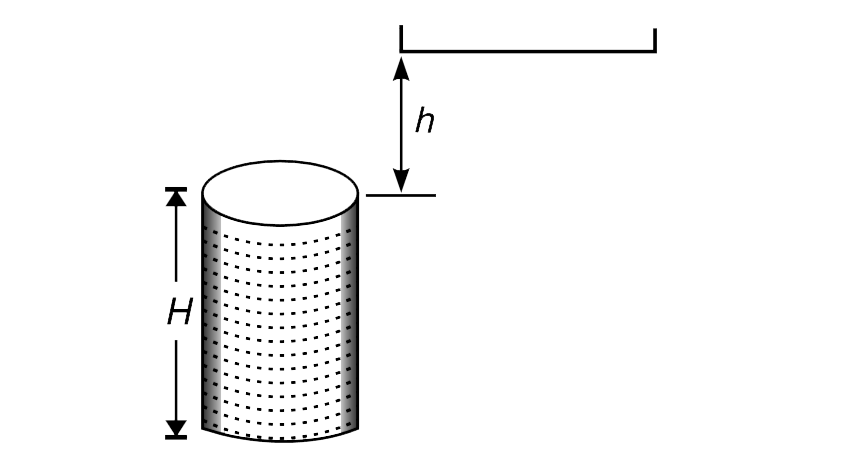
A cylindrical tank of height H is open at the top end and it has a radius r. Water is filled in it up to a height of h. The time taken to empty the tank through a hole of radius r' in its bottom is
√2hg(R2r2)
√2Hg(R2r2)
√h(H)
√2Hg(Rr)
The correct Answer is:A
−πR2dhdt=πr2√2ghordhdt=−r2R2√2gh
or dt=−R2r21√2ghdh∵∫t0dt=R2r2√2g∫0hh−1/2dh
or t=−R2r2√2g×2[√h]0hort=√2hg[R2r2]
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:integer Type Questions
Explore 25 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Level 1 (H.W)
Explore 55 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Paragraph Type Questions
Explore 5 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
A cylinderical tank of height 0.4 m is open at the top and has a diameter 0.16m. Water is filled in it up to height of 0.16 m. Find the time taken to empty the tank through a hole of radius 5×10−3m in its bottom.
View SolutionA cylindrical tank of height 2 m is open at the top and has a radius 50 cm. Water is filled in it upto a height 1.75 m. Calculate how long it will take to empty the tank through a hole of radius 0.05 cm in its bottom.
View Solution
Knowledge Check
A hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2A Water tank is 11m lengthy, 10m wich and 9 m high. The water has been filled i it up to the height of 6 m. How much parts of the tank is empty ?
A14B13C16D23A pipe can fill a tank in 10h , while an another pipe can empty it in 6h . Find the time taken to empty the tank , when both the pipes are opened up simultaneously .
A11hB15hC18hD16h
A completely filled cylinderical tank of height H contains water of mass M. At a height h above the top of the tank there is another wide container. The entire water from the tank is to be transferred into the container in time t0 such that level of water in tank decreases at a uniform rate. How will the power of the external agent vary with time?
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
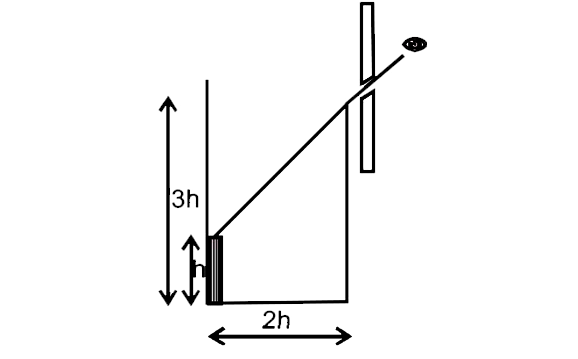
View SolutionAn observer can see through a pin-hole the top end of a thin of height h, places as shown in figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is

View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is

View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The height of beaker is 3h and its radius is h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
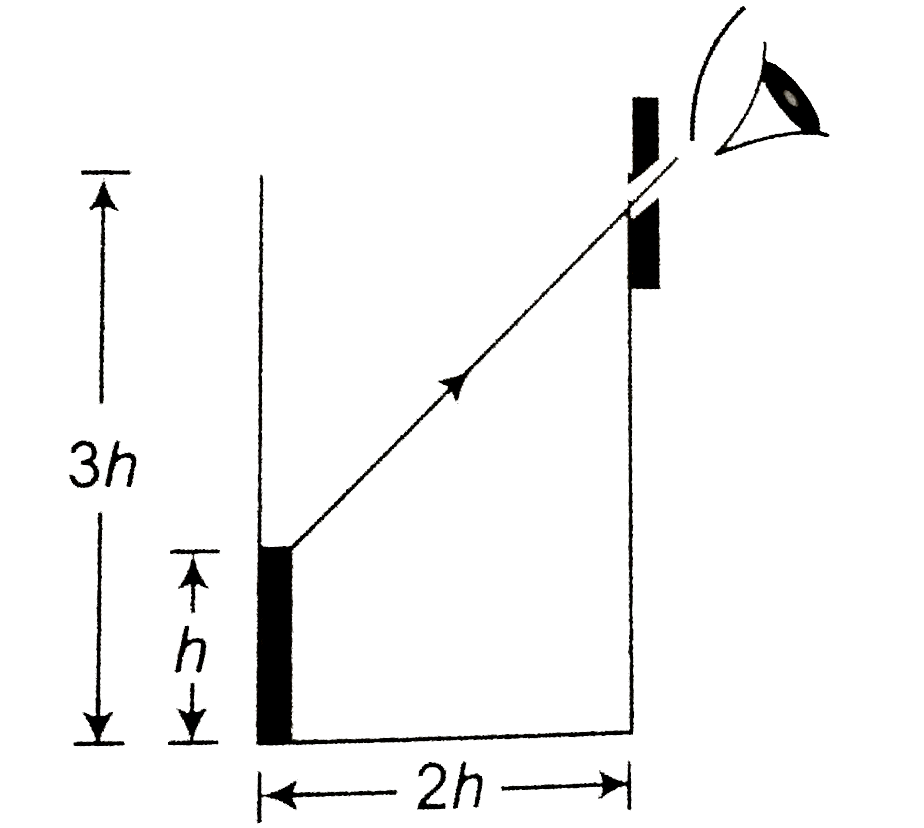
View Solution