A small cube of liquid of surface area $A$ ias considered at a depth of $' h'$ form the surface of liquid. If the density is $ρ$ bulk modulus is $B$ , the elastic energy density inside the cube is proportional to:"

A

$h^{2}$

B

$A$

C

$\frac{1}{B}$

D

$ρ$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C

$E = \frac{1}{2} \frac{{stress}^{2}}{B} = \frac{1}{2} \frac{p^{2}}{2} \frac{p^{2}}{B} = \frac{1}{2} \frac{h^{2} ρ^{2} g^{2}}{B}$

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The pressure at depth h below the surface of a liquid of density $ρ$ open to the atmosphere is
Agreater than the atmospheric pressure by $ρ g h$
Bless than the atmospheric pressure by $ρ g h$
Cequal to the atmospheric pressure
Dincreases exponentially with depth
Question 2 - Select One
If the atompspheric pressure is $P_{a}$ then the jpressure P at depth a below the surface of a liquid of density $ρ$ open to the atmosphere is
A $P_{a} - \frac{ρ g h}{2}$
B $P_{a} - ρ g h$
C $P_{a} + ρ g h$
D $P_{1} + \frac{ρ g h}{2}$
Question 3 - Select One
The liquid inside the container has density $ρ$ . Choose the correct option.

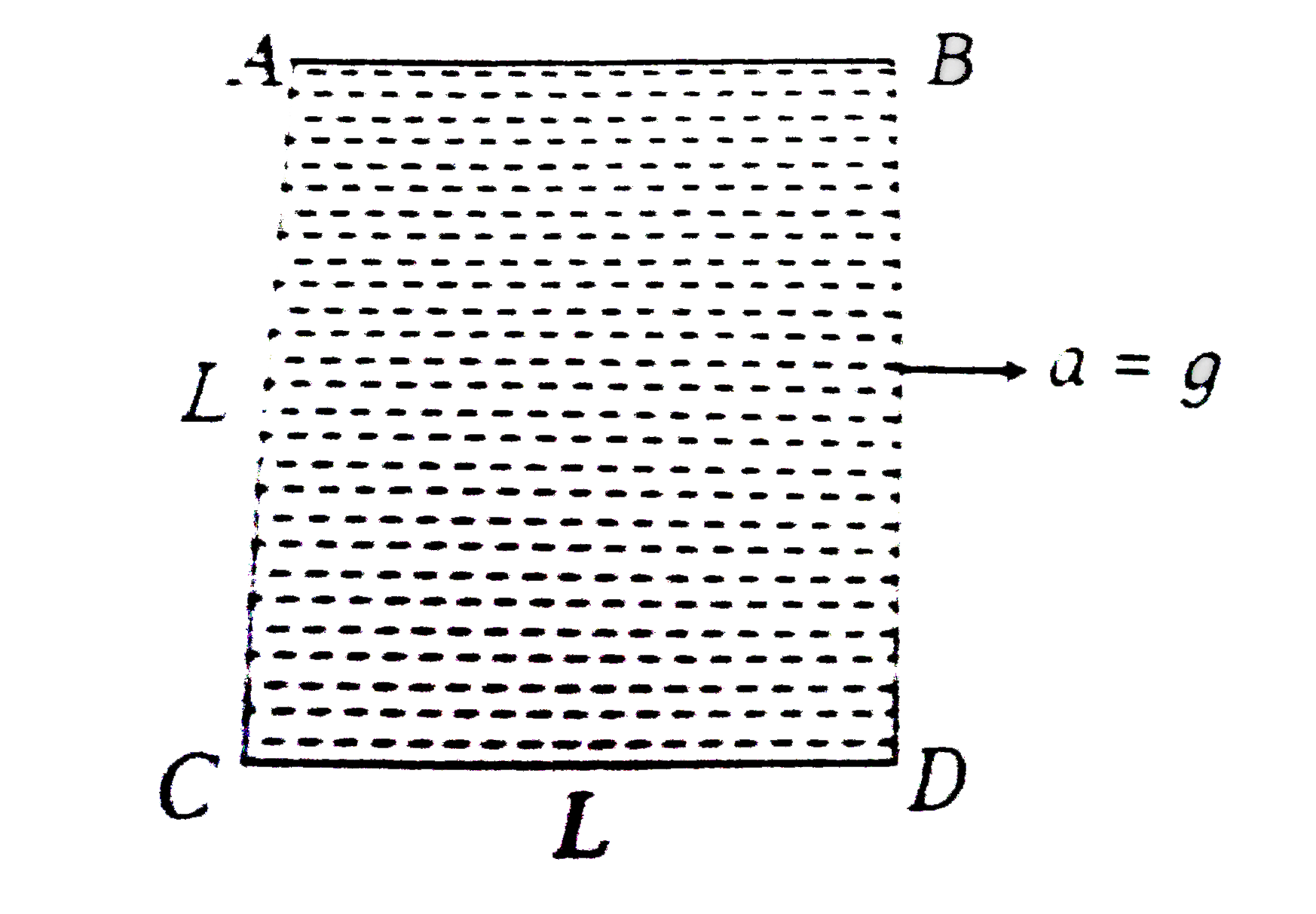A $p_{A} - p_{C} = 2 ρ g L$
B $p_{C} - p_{B} = \sqrt{2} ρ g L$
C $p_{C} - p_{D} = ρ g L$
D $p_{A} - p_{D} = 0 ρ g L$

NARAYNA-MECHANICAL PROPERTIES OF SOLIDS-MULTIPLE ANSWER TYPE

Home
Ask Doubt
Profile